The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process is
57
35
27
53
The correct Answer is:C
To find the ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process, we can follow these steps:
Step 1: Understand the First Law of Thermodynamics
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
Where:
- ΔQ is the heat supplied to the system,
- ΔU is the change in internal energy,
- ΔW is the work done by the system.
Step 2: Determine the Change in Internal Energy (ΔU)
For an ideal diatomic gas, the change in internal energy can be expressed as:
ΔU=nCvΔT
Where:
- n is the number of moles,
- Cv is the molar specific heat at constant volume,
- ΔT is the change in temperature.
For a diatomic gas, the degrees of freedom f is 5, so:
Cv=f2R=52R
Thus, we can write:
ΔU=n(52R)ΔT=52nRΔT
Step 3: Determine the Heat Supplied (ΔQ)
For an isobaric process, the heat supplied is given by:
ΔQ=nCpΔT
Where:
- Cp is the molar specific heat at constant pressure.
For a diatomic gas:
Cp=Cv+R=52R+R=72R
Thus, we can write:
ΔQ=n(72R)ΔT=72nRΔT
Step 4: Determine the Work Done (ΔW)
From the first law of thermodynamics, we can express the work done as:
ΔW=ΔQ−ΔU
Substituting the expressions for ΔQ and ΔU:
ΔW=72nRΔT−52nRΔT
ΔW=(72−52)nRΔT=22nRΔT=nRΔT
Step 5: Calculate the Ratio ΔWΔQ
Now we can find the ratio of work done to heat supplied:
ΔWΔQ=nRΔT72nRΔT
The nRΔT terms cancel out:
ΔWΔQ=172=27
Final Answer
The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process is:
27
The first law of thermodynamics states:
ΔQ=ΔU+ΔW
Where:
- ΔQ is the heat supplied to the system,
- ΔU is the change in internal energy,
- ΔW is the work done by the system.
For an ideal diatomic gas, the change in internal energy can be expressed as:
ΔU=nCvΔT
Where:
- n is the number of moles,
- Cv is the molar specific heat at constant volume,
- ΔT is the change in temperature.
Cv=f2R=52R
Thus, we can write:
ΔU=n(52R)ΔT=52nRΔT
For an isobaric process, the heat supplied is given by:
ΔQ=nCpΔT
Where:
- Cp is the molar specific heat at constant pressure.
Cp=Cv+R=52R+R=72R
Thus, we can write:
ΔQ=n(72R)ΔT=72nRΔT
From the first law of thermodynamics, we can express the work done as:
ΔW=ΔQ−ΔU
Substituting the expressions for ΔQ and ΔU:
ΔW=72nRΔT−52nRΔT
ΔW=(72−52)nRΔT=22nRΔT=nRΔT
Now we can find the ratio of work done to heat supplied:
ΔWΔQ=nRΔT72nRΔT
The nRΔT terms cancel out:
ΔWΔQ=172=27
The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process is:
27
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Application Of First Law Of Thermodynamics In Different Situations
25 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Second Law Of Thermodynamics
29 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Ideal Gas Equation
32 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
Similar Questions
The molar heat capacity for an ideal monatomic gas is 3R.If dQ is the heat supplied to the gas and dU is the change in its internal energy then for the process the ratio of work done by the gas and heat supplied is equal to
View SolutionA diatomic gas does 100 J of work when it is expanded isobarically. The heat given to the gas during this process is
View Solution
Knowledge Check
The ratio of work done by an ideal diatomic gas to the heat supplied by the gas in an isobaric process is
A57B35C27D53When heat in given to a gas in an isobaric process, then
AThe work is done by the gasBInternal energy of the gas increasesCBoth (a) and (b)DNone from (a) and (b)If heat is supplied to an ideal gas in an isothermal process.
Athe internal energy of the gas will increaseBthe gas will do positive workCthe gas will do negative workDthe said process is not possible.
If heat is supplied to an ideal gas in an isothermal process.
View SolutionWhen heat is supplied to an ideal gas in isothermal process, the
View Solutiongraph of an ideal gas is as shown in figure.
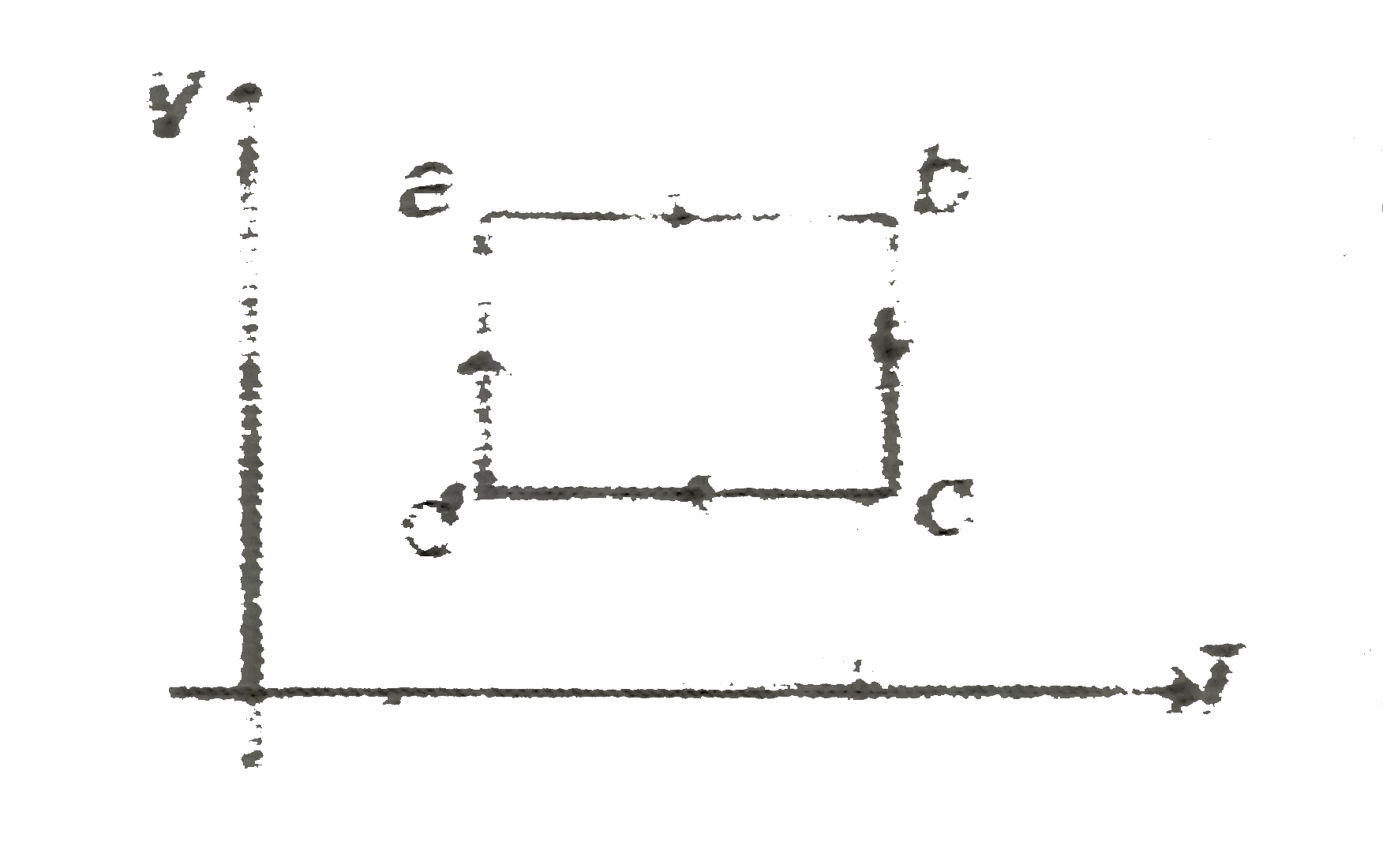
Heat is supplied to the gas in process (s).
View SolutionIn a isobaric process the work done by a di-atomic gas is 10 J , the heat given to the gas will be :
View SolutionA diatomic gas does 80 J of work when expanded isobarically. The heat given to the gas during this process is
View Solution
