The reading of a barometer containing some air above the mercury column is 73cm while that of a correct one is 76cm. If the tube of the faulty barometer is pushed down into mercury until volume of air in it is reduced to half, the reading shown by it will be:

70 cm

72 cm

74 cm

76 cm

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the situation of the faulty barometer and apply the ideal gas law. Here’s the step-by-step solution:
Step 1: Understand the Initial Conditions
The faulty barometer shows a reading of 73 cm of Hg, while the correct atmospheric pressure is 76 cm of Hg. This indicates that there is air trapped above the mercury column in the faulty barometer.
Step 2: Determine the Pressure of the Trapped Air
The pressure of the trapped air (P1) can be calculated using the difference between the atmospheric pressure and the reading of the faulty barometer:
$P_{1} = P_{a t m} - P_{f a u l t y} = 76 cm Hg - 73 cm Hg = 3 cm Hg$
Step 3: Analyze the Change in Volume of Air
When the tube of the faulty barometer is pushed down into the mercury, the volume of the trapped air is reduced to half. Let the initial volume of air be $V_{1}$ and the final volume be $V_{2} = \frac{V_{1}}{2}$ .
Step 4: Apply the Ideal Gas Law
Since the temperature remains constant and the number of moles of air does not change, we can use the ideal gas law for both conditions:
$P_{1} V_{1} = n R T (Condition 1)$
$P_{2} V_{2} = n R T (Condition 2)$
Setting these two equations equal gives:
$P_{1} V_{1} = P_{2} (\frac{V_{1}}{2})$
Step 5: Solve for $P_{2}$
Substituting $P_{1} = 3 cm Hg$ :
$3 cm Hg \cdot V_{1} = P_{2} \cdot \frac{V_{1}}{2}$
Cancelling $V_{1}$ from both sides (assuming $V_{1} \neq 0$ ):
$3 cm Hg = \frac{P_{2}}{2}$
Multiplying both sides by 2 gives:
$P_{2} = 6 cm Hg$
Step 6: Calculate the New Reading of the Barometer
The pressure at the mercury level must equal the atmospheric pressure:
$P_{a t m} = P_{2} + h$
Where $h$ is the height of the mercury column in the faulty barometer. Since $P_{a t m} = 76 cm Hg$ :
$76 cm Hg = 6 cm Hg + h$
Solving for $h$ :
$h = 76 cm Hg - 6 cm Hg = 70 cm Hg$
Conclusion
The reading shown by the faulty barometer after the volume of air is reduced to half will be:
$Final Reading = 70 cm Hg$

Updated on:18/9/2024

Class 12 PHYSICS Kinetic Theory of Gases and Gas Laws

Topper's Solved these Questions

Knowledge Check

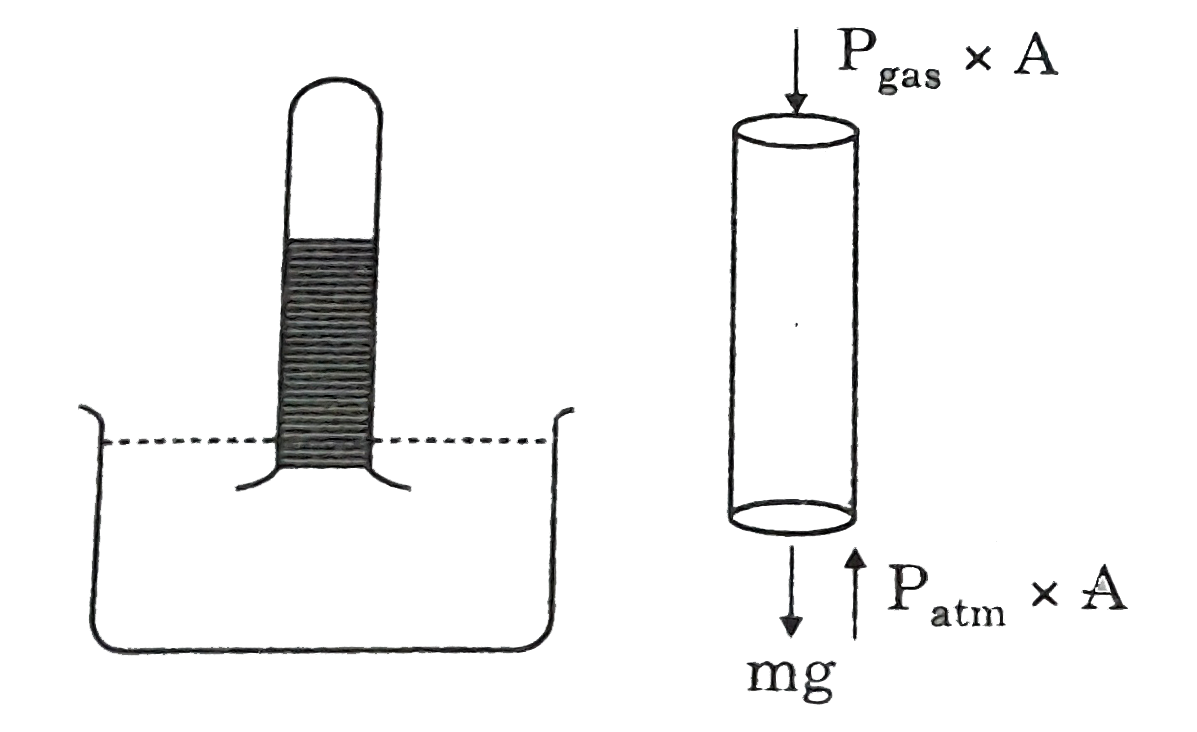
A barometer is an instrument that is used for the measurement of pressure The construction of the barometer is as follows:

A thin narrow calibrated capillary tube is filled to the brim with a liquid such as mercury and is inverted into a through filled with the same fluid Now depending on the external atmospheric pressure the level of the inside capillary comes to rest, then the net forces on the column should be balanced Applying force balance we get $P_{a t m} \times A = m \times g$
(A is the cross-sectional area of the capillary tube) if $ρ$ is the density of the fluid, then $m = ρ \times g \times h$
(h is the height to which mercury has risen in the capillary)
Hence $P_{a t m} \times A = (ρ \times g \times h) \times A or P_{a t m} = ρ g h$
Faulty Barometer:
An ideal barometer will show a correct reading only if the space above the mercury column is vacuum but in case if some gas column is trapped in the space above the mercury column then the barometer is classified as a faulty barometer. The reading of such a barometer will be less than the true pressure

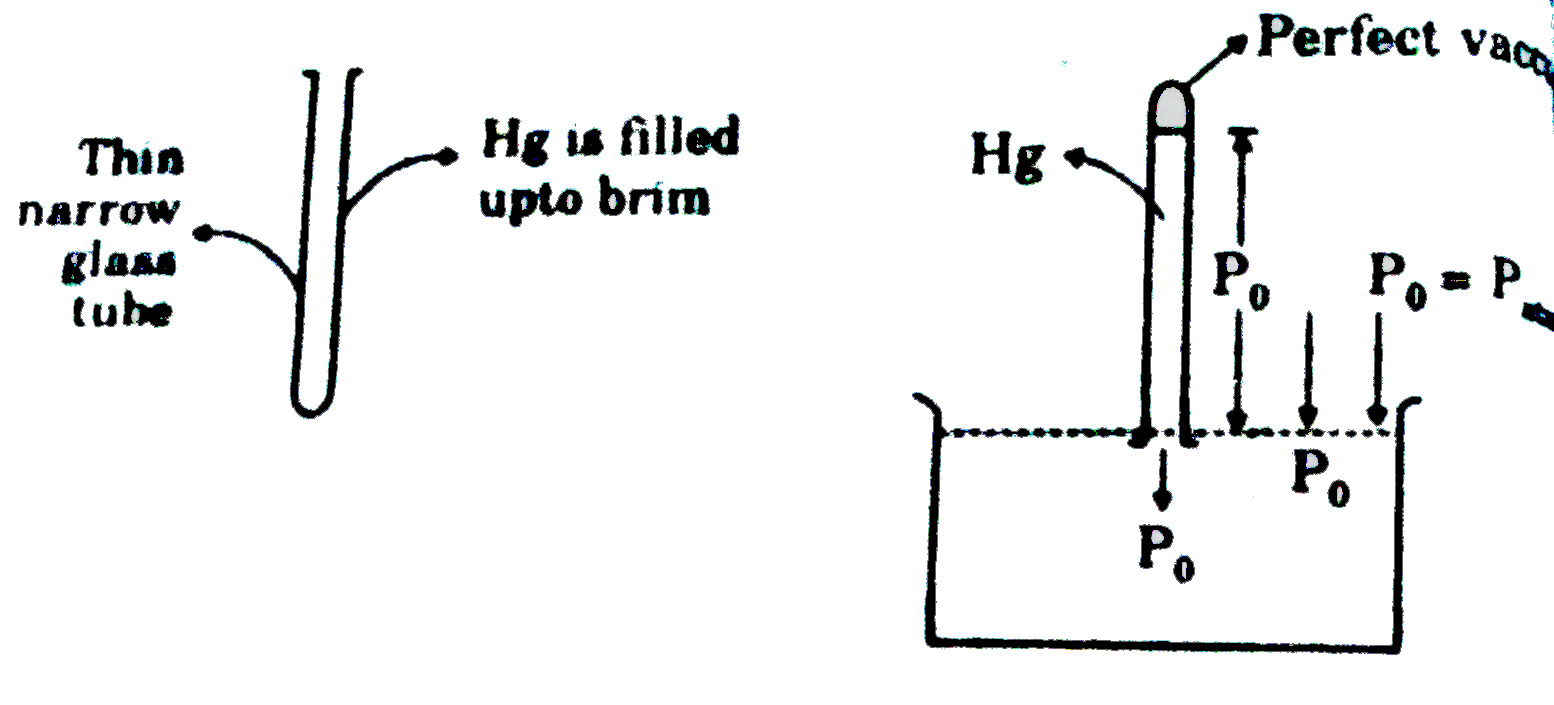
For such a faulty barometer
$P_{0} A = m g + P_{g a s} A$
$P_{0} = ρ h g + P_{g a s}$
or $ρ g h = P_{0} - P_{g a s}$
A tube closed at one end is dipped in mercury as shown in figure such that the closed surface coincides with the mercury level in the container By how much length of the tube should be extended such that the level of Hg in the tube is 5 cm below the mercury level inside the container? (Assume temperature remains constant)

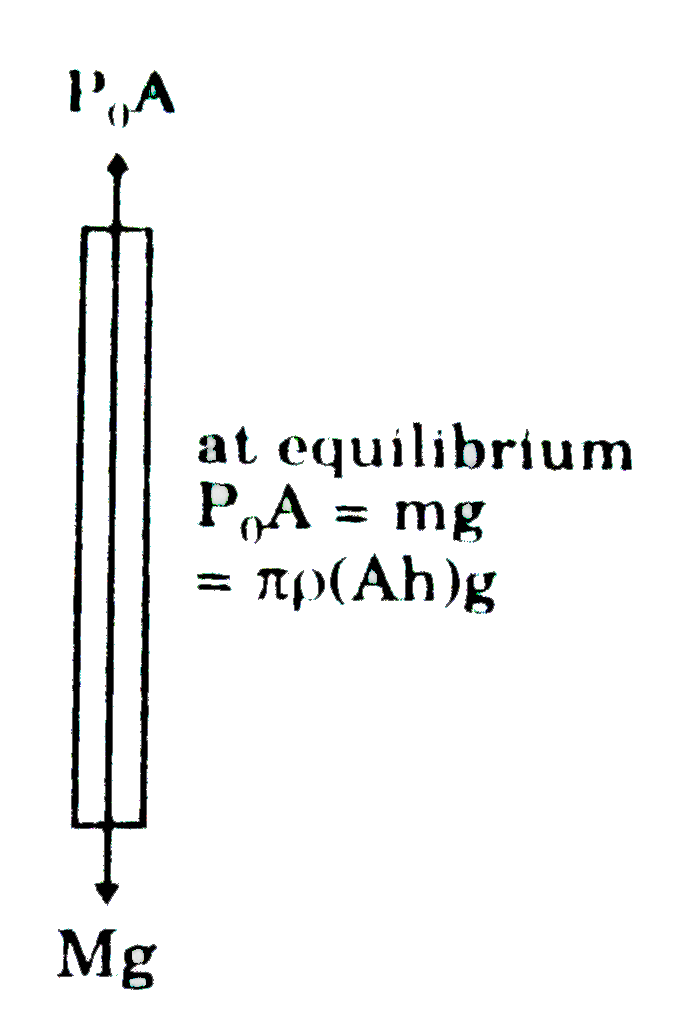
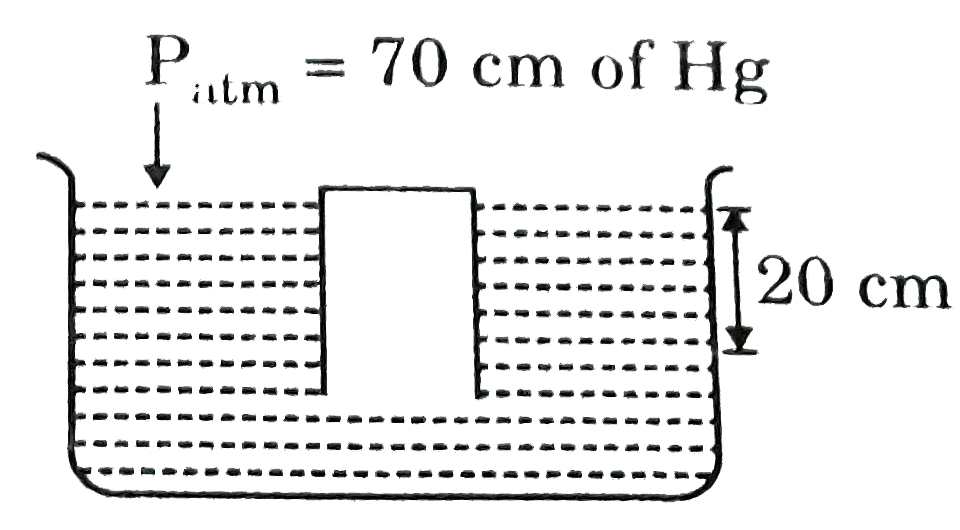A18 cm
B19 cm
C24 cm
D30 cm
A barometer is an instrument that is used for the measurement of pressure The construction of the barometer is as follows:

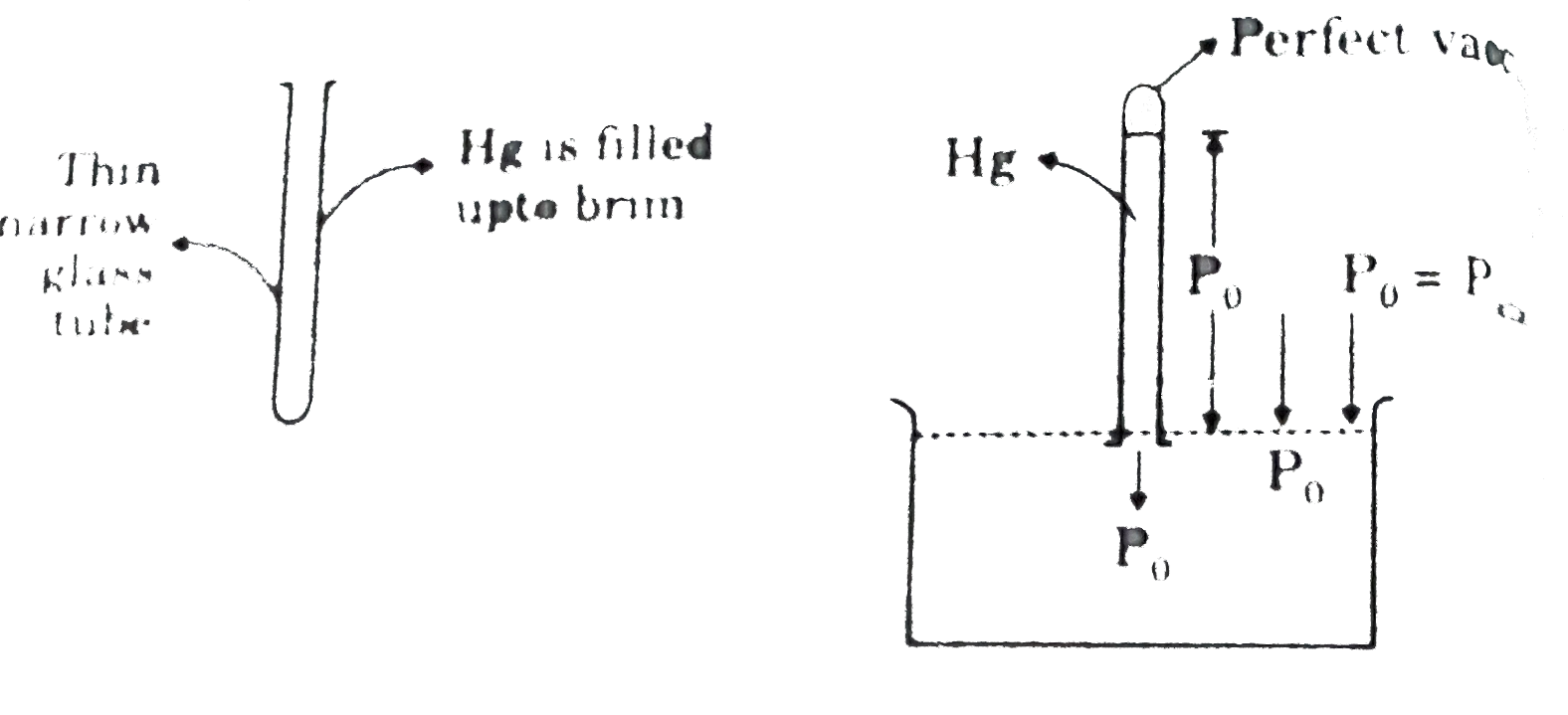
A thin narrow calibrated capillary tube is filled to the brim with a liquid such as mercury and is inverted into a through filled with the same fluid Now depending on the external atmospheric pressure the level of the inside capillary comes to rest, then the net forces on the column should be balanced Applying force balance we get $P_{a t m} \times A = m \times g$
(A is the cross-sectional area of the capillary tube) if $ρ$ is the density of the fluid, then $m = ρ \times g \times h$
(h is the height to which mercury has risen in the capillary)
Hence $P_{a t m} \times A = (ρ \times g \times h) \times A or P_{a t m} = ρ g h$
Faulty Barometer:
An ideal barometer will show a correct reading only if the space above the mercury column is vacuum but in case if some gas column is trapped in the space above the mercury column then the barometer is classified as a faulty barometer. The reading of such a barometer will be less than the true pressure
For such a faulty barometer
$P_{0} A = m g + P_{g a s} A$
$P_{0} = ρ h g + P_{g a s}$
or $ρ g h = P_{0} - P_{g a s}$
If the tube shown below is placed vertically with the open and upward then the length of the air column will be (Assume temperature remains constant)

A20 cm
B36 cm
C18 cm
D15 cm
The height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ratio of density of mercury to that of air is 10. The height of the hill is
A $250 m$
B $2.5 k m$
C $1.25 k m$
D $750 k m$

PHYSICS GALAXY - ASHISH ARORA-Kinetic Theory of Gases and Gas Laws-Numerical MCQs Single Options Correct

Home
Ask Doubt
Profile

The reading of a barometer containing some air above the mercury column is 73cm while that of a correct one is 76cm. If the tube of the faulty barometer is pushed down into mercury until volume of air in it is reduced to half, the reading shown by it will be:

Topper's Solved these Questions

Similar Questions

Knowledge Check

The height of a mercury barometer is 75 cm at sea level and 50 cm at the top of a hill. Ratio of density of mercury to that of air is 10. The height of the hill is

PHYSICS GALAXY - ASHISH ARORA-Kinetic Theory of Gases and Gas Laws-Numerical MCQs Single Options Correct