The resultant of two vector A and B is at right angles to A and its magnitude is half of B. Find the angle between A and B.
120∘
150∘
135∘
None of these
The correct Answer is:B
B2=√A2+B2+2ABcosθ…..(i)
∴Tan90∘=BsinθA+Bcosθ⇒A+Bcosθ=0
∴cosθ=−AB
Hence, from (i), B24=A2+B2−2A2⇒A=√3B2
⇒cosθ=−AB=−√32,∴θ=150∘
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Expressing Vectors In Unit Vector Notation22videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Dot Product22videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test29videos
VECTORS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
The resultant of two vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between A and B is -
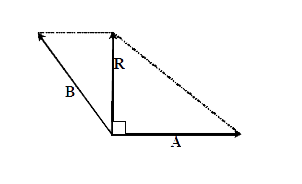 View Solution
View SolutionFind the magnitude and direction of the resultant of two vectors A and B in the terms of their magnitudes and angle θ between them.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The sum of two vectors A and B is at right angles to their difference. Then
AA=BBA=2BCB=2ADA and B have the same direction - Question 2 - Select One
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-
A120∘B150∘C135∘DNone of these - Question 3 - Select One
The resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
A30∘B45∘C150∘D120∘
The resultant of two vectors u and v is perpendicular to the vector u and its magnitude is equal to half of the magnitude of vector v. Find the angle between u and v.
View SolutionThe resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View SolutionMagnitude of resultant of two vectors →P and →Q is equal to magnitude of →P . Find the angle between →Q and resultant of →2P and →Q .
View SolutionThe resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
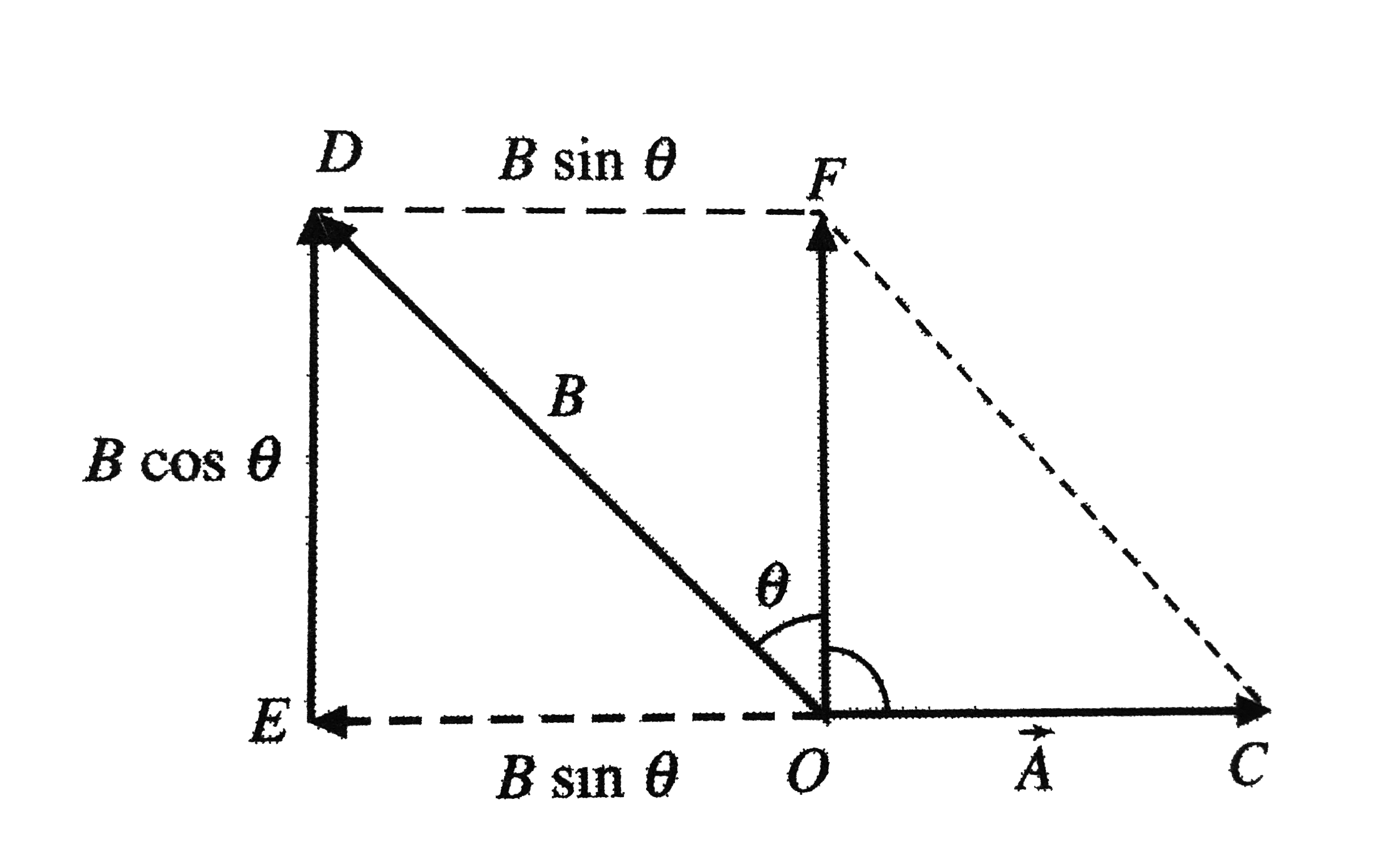 .View Solution
.View Solution

