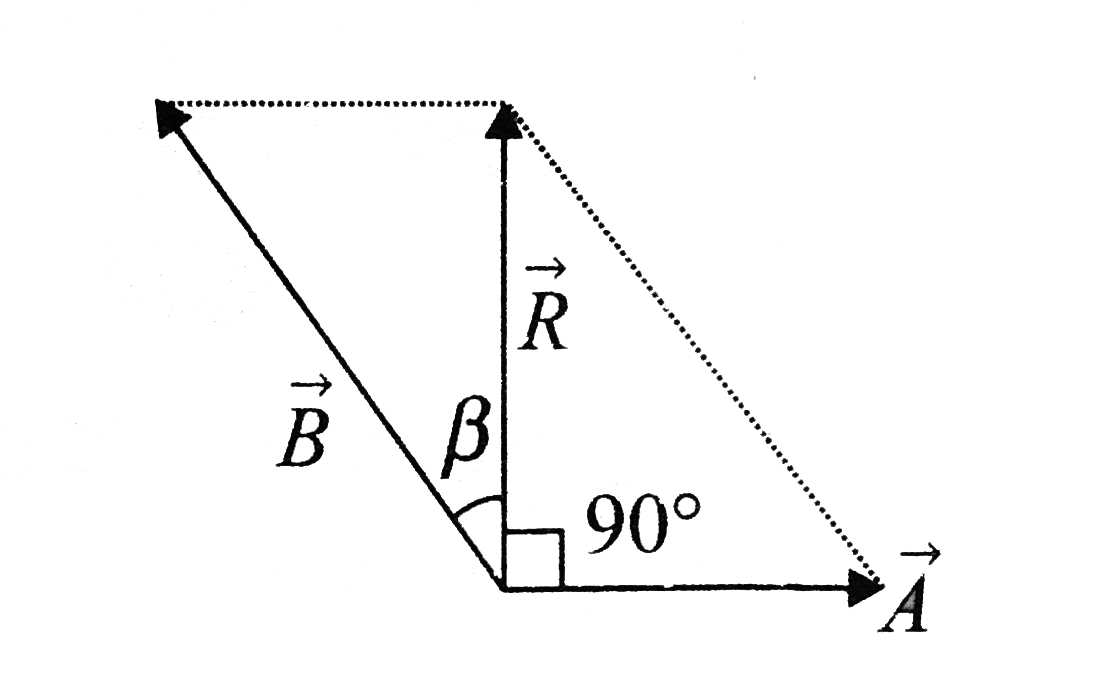
The resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
30∘
45∘
150∘
120∘
The correct Answer is:C
To solve the problem step by step, we will analyze the information given and use vector properties to find the angle between vectors →A and →B.
Step 1: Understand the Given Information
We know that:
- The resultant vector →R of vectors →A and →B is perpendicular to →A.
- The magnitude of →R is equal to half the magnitude of →B, i.e., |→R|=12|→B|.
Step 2: Set Up the Vector Equation
The resultant vector →R can be expressed as:
→R=→A+→B
Since →R is perpendicular to →A, we can use the dot product:
→R⋅→A=0
Step 3: Substitute →R in the Dot Product
Substituting →R:
(→A+→B)⋅→A=0
Expanding this gives:
→A⋅→A+→B⋅→A=0
Let |→A|=A and |→B|=B. Thus, we can write:
A2+B⋅Acos(θ)=0
where θ is the angle between →A and →B.
Step 4: Use the Magnitude of →R
The magnitude of →R can also be expressed using the law of cosines:
|→R|2=|→A|2+|→B|2+2|→A||→B|cos(θ)
Given |→R|=12B, we have:
(12B)2=A2+B2+2ABcos(θ)
This simplifies to:
14B2=A2+B2+2ABcos(θ)
Step 5: Rearranging the Equation
Rearranging gives:
14B2−B2=A2+2ABcos(θ)
−34B2=A2+2ABcos(θ)
Step 6: Solve for cos(θ)
From the previous equation, we can isolate cos(θ):
2ABcos(θ)=−34B2−A2
cos(θ)=−34B2−A22AB
Step 7: Find the Angle θ
From the earlier derived equations, we know that →A⋅→B=−A2. If we assume A=B for simplicity, we can find:
cos(θ)=−34
Using the inverse cosine function, we can find θ:
θ=cos−1(−34)
Step 8: Calculate the Angle
Using trigonometric identities, we can find that:
θ=150∘
Conclusion
The angle between vectors →A and →B is 150∘.
We know that:
- The resultant vector →R of vectors →A and →B is perpendicular to →A.
- The magnitude of →R is equal to half the magnitude of →B, i.e., |→R|=12|→B|.
The resultant vector →R can be expressed as:
→R=→A+→B
Since →R is perpendicular to →A, we can use the dot product:
→R⋅→A=0
Substituting →R:
(→A+→B)⋅→A=0
Expanding this gives:
→A⋅→A+→B⋅→A=0
Let |→A|=A and |→B|=B. Thus, we can write:
A2+B⋅Acos(θ)=0
where θ is the angle between →A and →B.
The magnitude of →R can also be expressed using the law of cosines:
|→R|2=|→A|2+|→B|2+2|→A||→B|cos(θ)
Given |→R|=12B, we have:
(12B)2=A2+B2+2ABcos(θ)
This simplifies to:
14B2=A2+B2+2ABcos(θ)
Rearranging gives:
14B2−B2=A2+2ABcos(θ)
−34B2=A2+2ABcos(θ)
From the previous equation, we can isolate cos(θ):
2ABcos(θ)=−34B2−A2
cos(θ)=−34B2−A22AB
From the earlier derived equations, we know that →A⋅→B=−A2. If we assume A=B for simplicity, we can find:
cos(θ)=−34
Using the inverse cosine function, we can find θ:
θ=cos−1(−34)
Using trigonometric identities, we can find that:
θ=150∘
The angle between vectors →A and →B is 150∘.
Topper's Solved these Questions
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - MULTIPLE CHOICE QUESTIONS (STANDARD LEVEL)
84 Videos
- VECTORSBOOK - MARVEL PUBLICATIONCHAPTER - VECTORSEXERCISE - TEST YOUR GRASP
10 Videos
- REFRACTION OF LIGHT BOOK - MARVEL PUBLICATIONCHAPTER - REFRACTION OF LIGHT EXERCISE - Test Your Grasp
10 Videos
Similar Questions
The resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionThe resultant of two velocity vectors →A and →B is perpendicular to →A. Magnitude of Resultant →R is equal to half magnitude of →B. If the angle between →A and →B is (30θ)∘, then value of θ is ?
View Solution
Knowledge Check
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of theseTwo vectors →A and →B have equal magnitudes. If magnitude of →A−→B is equal to (n) times the magnitude of →A−→B, then angle between →A and →B is ?
Acos−1(n−1n−1)Bcos−1(n2−1n2+1)Ccos−1(n−1n−1)Dcos−1(n2−1n2+1)Two vector →Vand→V have equal magnitudes. If magnitude of →A+→B is equal to n time the magnitude of →A−→B, then angel to between →Aand→B is
Acos−1(n−1n+1)Bcos−1(n2−1n2+1)Csin−1(n−1n+1)Dsin−1(n2−1n2+1)
Three vectors →A,→B and →C are related as →A+→B=→C .If vector →C is perpendicular to vector →A and the magnitude of →C is equal to the magnitude of →A, what will be the angle between vectors →A and →B.
View SolutionTwo vectors →Aand→B have equal magnitudes.If magnitude of (→A+→B) is equal to n times of the magnitude of (→A−→B) then the angle between →Aand→B is :-
View SolutionTwo vectors vec A and vec B have equal magnitudes.The magnitude of (vec A+vec B) is 'n' times the magnitude of (vec A-vec B).The angle between vec A and vec B is:
View SolutionIf a,b,c are three mutually perpendicular vector each of magnitude unity, then what is the magnitude of ∣∣→a+→b+→c∣∣?
View SolutionTwo vectors →a and →b are such that ∣∣→a+→b∣∣=∣∣→a−→b∣∣. What is the angle between →a and →b?
View Solution
