The root mean square value of the alternating current is equal to
Twice the peak value
Half the peak value
times the peak value
Equal to the peak value
The correct Answer is:C
To find the root mean square (RMS) value of an alternating current (AC), we can follow these steps:
1. Understand the AC Current Equation:
The alternating current can be expressed as:
I(t)=I0cos(ωt+ϕ)
where I0 is the peak current, ω is the angular frequency, and ϕ is the phase difference.
2. Define RMS Current:
The root mean square (RMS) value of the current is defined as:
Irms=√1T∫T0I2(t)dt
where T is the time period of the AC signal.
3. Substitute the Current Equation:
Substitute I(t) into the RMS formula:
Irms=√1T∫T0(I0cos(ωt+ϕ))2dt
4. Simplify the Integral:
This simplifies to:
Irms=√I20T∫T0cos2(ωt+ϕ)dt
5. Evaluate the Integral:
The integral of cos2 over one complete cycle (time period T) is:
∫T0cos2(ωt+ϕ)dt=T2
Therefore, substituting this back into the equation gives:
Irms=√I20T⋅T2=√I202=I0√2
6. Final Result:
Thus, the root mean square value of the alternating current is:
Irms=I0√2
The alternating current can be expressed as:
I(t)=I0cos(ωt+ϕ)
where I0 is the peak current, ω is the angular frequency, and ϕ is the phase difference.
The root mean square (RMS) value of the current is defined as:
Irms=√1T∫T0I2(t)dt
where T is the time period of the AC signal.
Substitute I(t) into the RMS formula:
Irms=√1T∫T0(I0cos(ωt+ϕ))2dt
This simplifies to:
Irms=√I20T∫T0cos2(ωt+ϕ)dt
The integral of cos2 over one complete cycle (time period T) is:
∫T0cos2(ωt+ϕ)dt=T2
Therefore, substituting this back into the equation gives:
Irms=√I20T⋅T2=√I202=I0√2
Thus, the root mean square value of the alternating current is:
Irms=I0√2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The rms value of an alternating current
Ais equal to 0.707 times peak valueBis equal to 0.636 times peak valueCis equal sqrt2 times the peak valueDnone of the aboveThe root-mean-square value of an alternating current of 50 Hz frequency is 10 ampere. The time taken by the alternating current in reaching from zero to maximum value and the peak value of current will be
A2×10−2secand14.14ampB1×10−2secand7.07ampC5×10−3secand7.07ampD5×10−3secand14.14ampFigure shows one cycle of an alternating current with the segments AB, BC, CD, DE being symmetrical and parabolic. The root mean square value of this current over one cycle is x mA, find x.
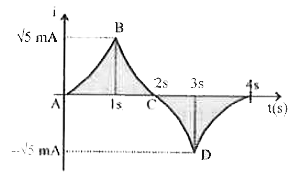 A1 mAB2 mAC3 mAD4 mA
A1 mAB2 mAC3 mAD4 mA
.What is meant by root mean square value of alternating current? Derive an expression of r .m.s value of A.C
View SolutionThe root mean square rm.s. value of alternating current I=60sin100nt is
View SolutionThe root mean square (r.m.s .) value of alternating current I=60sin100 pi(t) is
View SolutionThe root mean square r.m.s.value of alternating current I=60sin100 pi t is
View SolutionWhat is the root mean square value of current of effective current of an a.c. having a peak value of 5.0 amp? What will be the reading shown for this current by (i) an a.c. ammeter (ii) an ordinary moving coil ammeter ?
View Solution
