The simple pendulum of the previous problem is placed in uniform electric field E, directed horizontally. Find the angle made by string with vertical in equilibrium and tension in the string . Now the ball is slightly displaced and it exceutes simple harmonic motion, find its time period of oscillation.
The ball is in equilibrium under three forces
(a) Weight of ball mg
(b) Electric force qE
(c ) Tension in the string T
tanθ=qEmg⇒θ=tan−1(qEmg)
T=√(mg)2+(qE)2
For time period :
effective acceleration a==√(mg)2+(qE)2m
Time period T'=2π√La
=2π
⎷L[g2+(qEm)2]12

Topper's Solved these Questions
Similar Questions
A pedulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road Find the angle made by the string with vertical at equilibrium Also find the tension in the string in this position
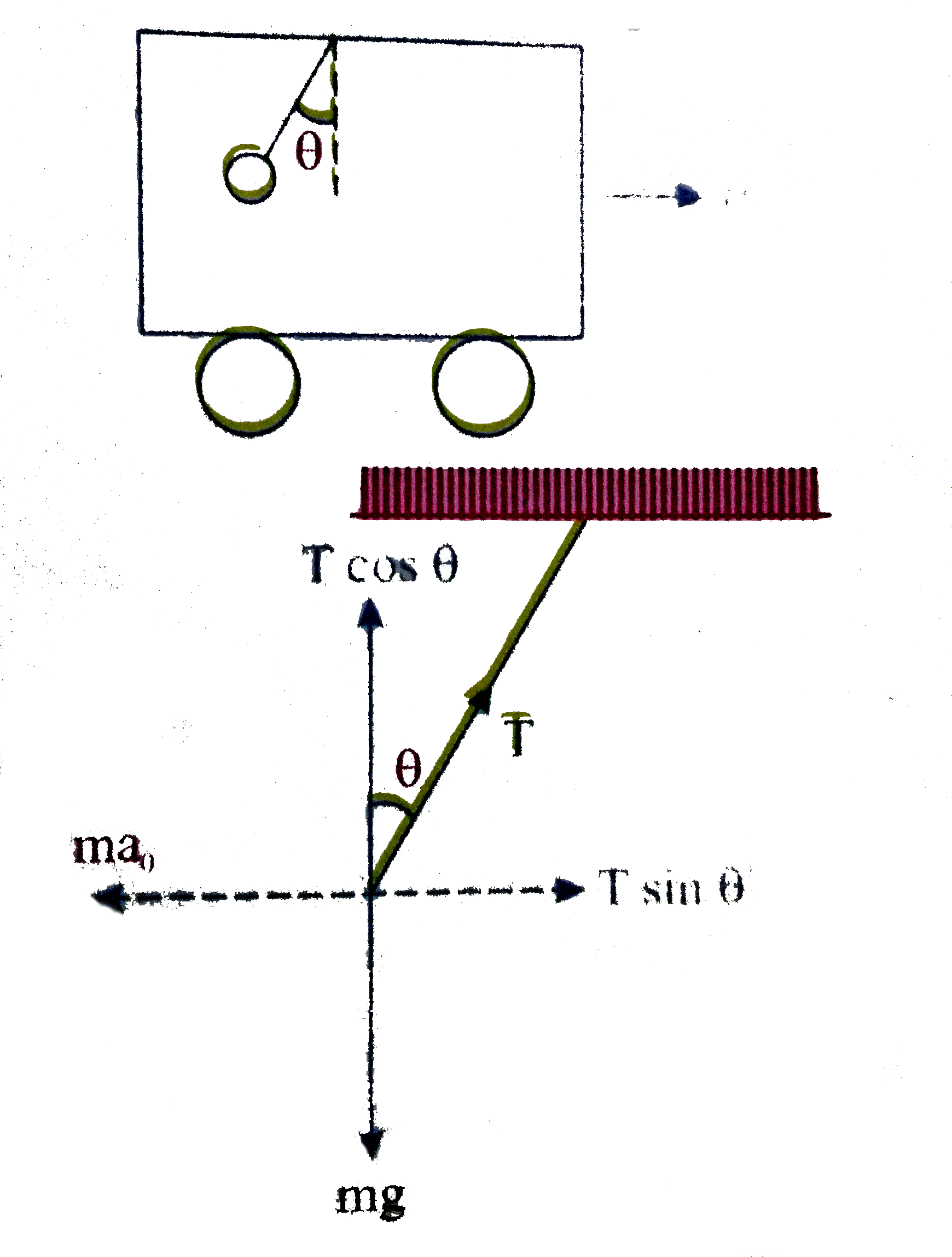 .
.
View SolutionFigure shows the graph of velocity versus displacement of a partciel executing simple harmonic motion. Find the period of oscillation of the particle.

View Solution
Knowledge Check
A mass m carrying a charge q si suspended form a string and placed in a uniform horizontal electric field of intensity E.The angel made by the string with the vertical in the equilibrium position is
Aθ=tan−1mgEqBθ=tan−1mEqCθ=tan−1EqmDθ=tan−1EqmgAn electric dipole of dipole moment p is placed in a uniform electric field E in stable equilibrium position. Its moment of inertia about the centroidal axis is I . If it is displaced slightly from its mean position, find the period of small oscillations.
Aπ√IpEB2π√IpECπ√2IpED2π√2IpEIf a simple pendulum has charge q and is oscillating in a uniform electric field E in the direction of acceleration due to gravity, then its frequency of oscillations
AincreasesBdecreasesCfirst increases and later on it remains constantDindependent of the effect of electric field
A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Findthe angle made by the string with the vertical.
View SolutionConsider the situation of the previous problum. (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
View Solutioncalculate the tension in the string and angle made by it with vertical if electric field is directed in horizontal direction.
View SolutionIn the previous problem , the block of massM is attached to a string of length L. Find the maximum angle made by the string with vertical . Take veloctiy of buller u=4√gL. Take M=3m.
View SolutionMass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
View Solution
