The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convex lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image
1.25cm
2.5cm
1.05cm
2cm
The correct Answer is:B
Convex lens will form image I1 at its focus which acts like a virtual object for concave lens.
Hence for concave lens u=+4cm,f=20cm. So by lens formula 1−20=1v−14⇒v=5cm i.e. distance of final image (I1) from concave lens v=5cm by using vu=IO⇒54⇒(I2)=2.5cm
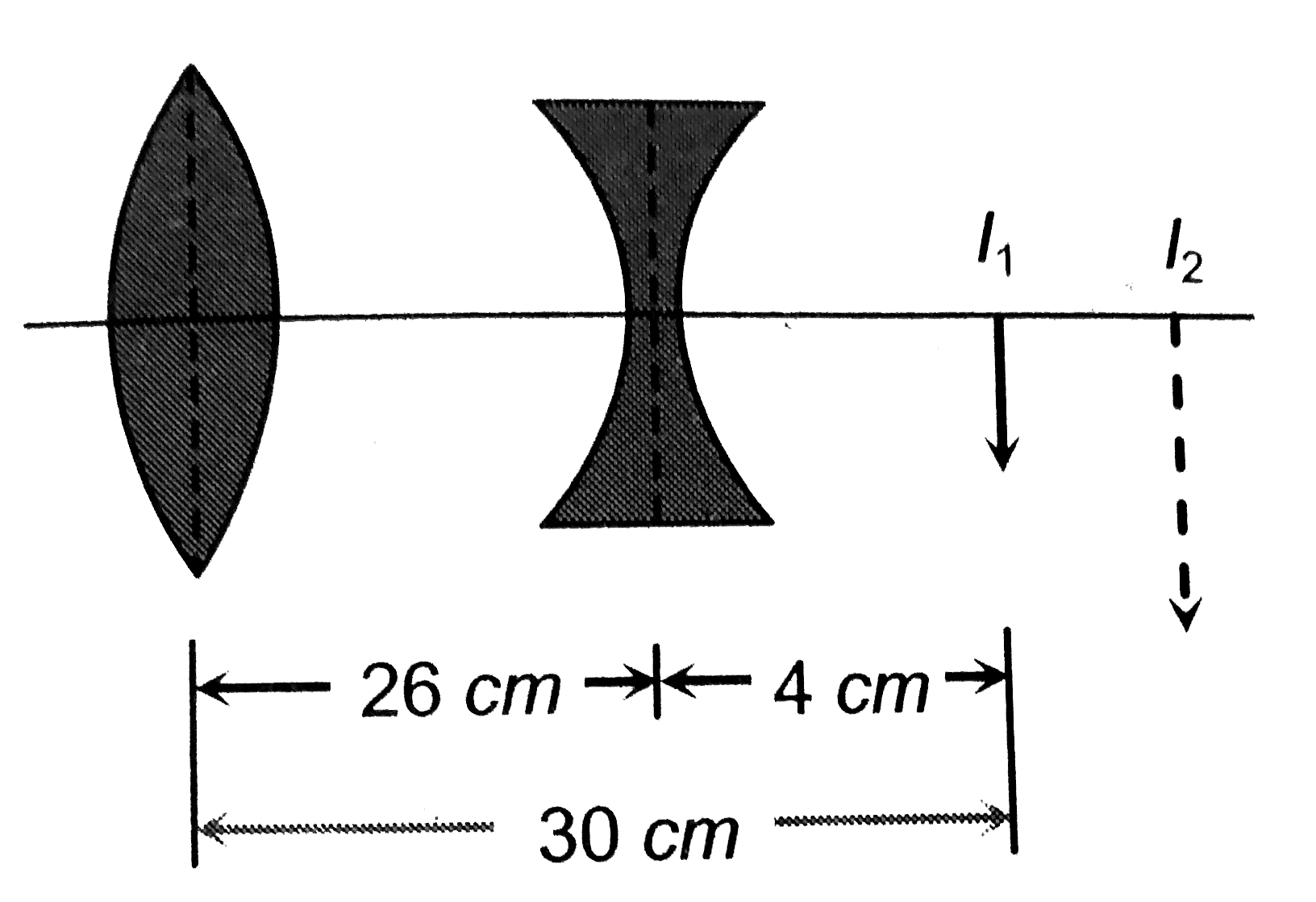
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section B - Assertion Reasoning19videos
GEOMETRICAL OPTICS
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - AIPMT/NEET Questions95videos
GEOMETRICAL OPTICS
- BOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Optical Instruments55videos
GEOMETRICAL OPTICS
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM
- BOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test30videos
MAGNETISM AND MATTER
Similar Questions
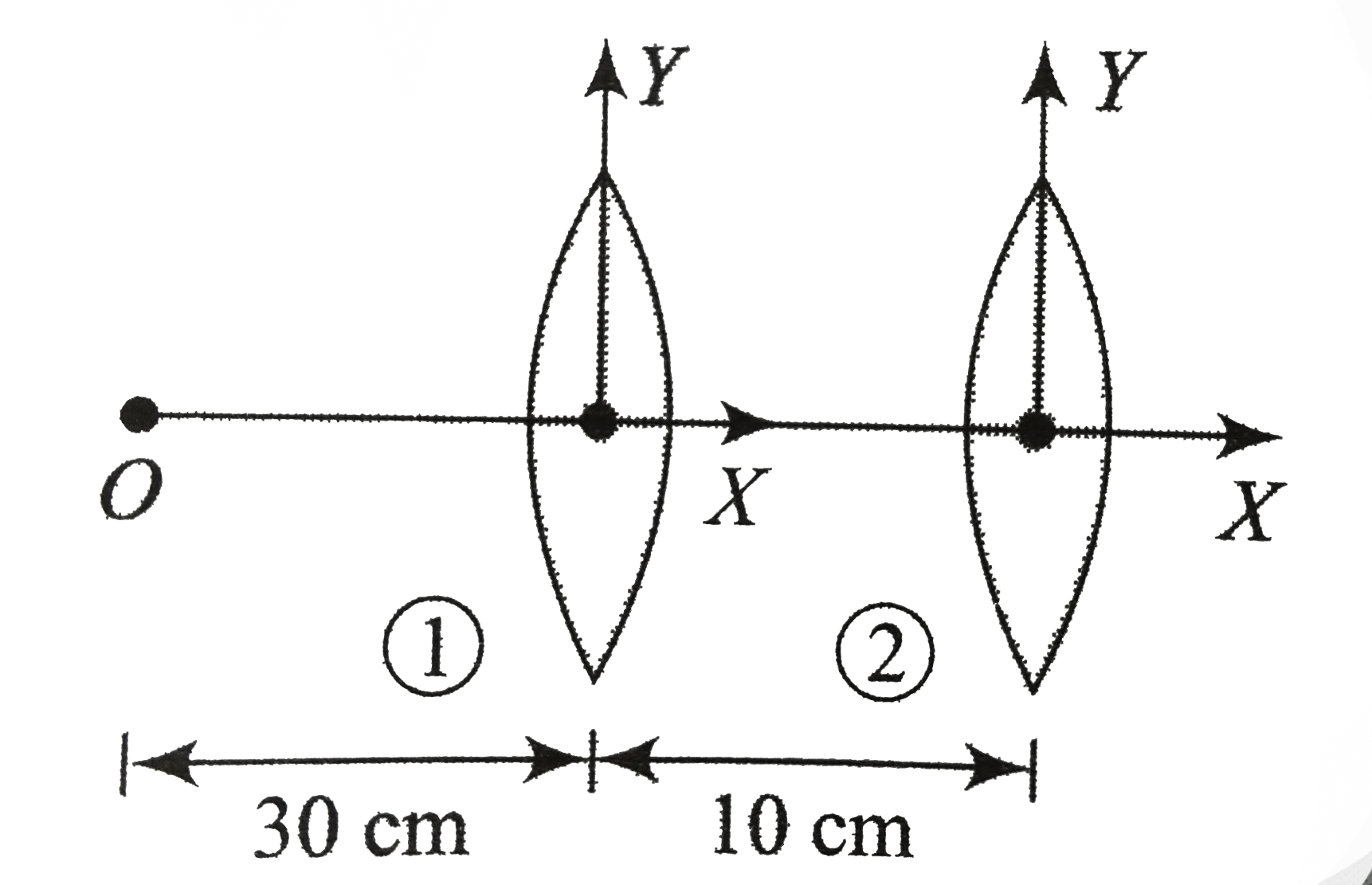
A convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?
 View Solution
View SolutionAn object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.Find the position of the image .
View Solution
Knowledge Check
- Question 1 - Select One
The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30cm is 2cm. If a concave lens of focal length 20cm is placed between the convex lens and the image at a distance of 26cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cm - Question 2 - Select One
The size of the image of an object,which is at infinity, as formed by a convex lens of focal length 20 cm is placed between the convex lens and the image at the distance of 26 cm from the convex lens, the new size of the image is
A1.25 cmB2.5 cmC1.05 cmD2 cm - Question 3 - Select One
A convex lens of focal length 30 cm forms an image of height 2 cm for an object situated at infinity. If a concave lens of focal length 20 cm is placed coaxially at a distance of 26 cm from convex lens then size of image would be
A2.5cmB5.0cmC1.25cmD4cm
A convex lens of focal length 30cm and a concave lens of focal length 60cm are placed in combination. If an object is placed 40cm away from the combination, find the position of the image.
View SolutionA convex lens of focal length 0.10 cm is used to form a magnified image of an object of height 5 mm placed a distance of 0.08 m form the lens. Calculate the position, nature and size of the image.
View SolutionWhat is the position of image when an object is placed is at a distance of 10 cm from a convex lens of focal length 10 cm?
View SolutionA convex lens of focal length 16 cm forms a real image double the size of the object. The image distance of the object from the lens is
View SolutionA plano-convex lens of focal length 30 cm has its plane surface silvered. An object is placed 40 cm from the lens on the convex side. The distance of the image from the lens is
View Solution

