The speed of rolling of a ring of mass m changes from V to 3V . What is the change in its kinetic energy
3MV2
4MV2
6MV2
8MV2
The correct Answer is:D
To find the change in kinetic energy of a ring of mass m when its speed changes from V to 3V, we need to consider both the translational and rotational kinetic energy of the ring.
1. Identify the Kinetic Energy Components:
The total kinetic energy K of the ring is the sum of its translational kinetic energy Ktrans and its rotational kinetic energy Krot:
K=Ktrans+Krot
2. Calculate the Initial Kinetic Energy:
- The translational kinetic energy when the speed is V:
Ktrans,initial=12mV2
- The moment of inertia I of a ring about its center is I=mR2.
- The angular velocity ω can be expressed in terms of V:
ω=VR
- The rotational kinetic energy is given by:
Krot,initial=12Iω2=12(mR2)(VR)2=12mV2
- Therefore, the total initial kinetic energy Kinitial is:
Kinitial=Ktrans,initial+Krot,initial=12mV2+12mV2=mV2
3. Calculate the Final Kinetic Energy:
- The translational kinetic energy when the speed is 3V:
Ktrans,final=12m(3V)2=12m(9V2)=92mV2
- The angular velocity at this speed is:
ω=3VR
- The rotational kinetic energy is:
Krot,final=12Iω2=12(mR2)(3VR)2=12(mR2)(9V2R2)=92mV2
- Therefore, the total final kinetic energy Kfinal is:
Kfinal=Ktrans,final+Krot,final=92mV2+92mV2=9mV2
4. Calculate the Change in Kinetic Energy:
The change in kinetic energy ΔK is given by:
ΔK=Kfinal−Kinitial=9mV2−mV2=8mV2
Final Answer:
The change in kinetic energy is ΔK=8mV2.
---
The total kinetic energy K of the ring is the sum of its translational kinetic energy Ktrans and its rotational kinetic energy Krot:
K=Ktrans+Krot
- The translational kinetic energy when the speed is V:
Ktrans,initial=12mV2
- The moment of inertia I of a ring about its center is I=mR2.
- The angular velocity ω can be expressed in terms of V:
ω=VR
- The rotational kinetic energy is given by:
Krot,initial=12Iω2=12(mR2)(VR)2=12mV2
- Therefore, the total initial kinetic energy Kinitial is:
Kinitial=Ktrans,initial+Krot,initial=12mV2+12mV2=mV2
- The translational kinetic energy when the speed is 3V:
Ktrans,final=12m(3V)2=12m(9V2)=92mV2
- The angular velocity at this speed is:
ω=3VR
- The rotational kinetic energy is:
Krot,final=12Iω2=12(mR2)(3VR)2=12(mR2)(9V2R2)=92mV2
- Therefore, the total final kinetic energy Kfinal is:
Kfinal=Ktrans,final+Krot,final=92mV2+92mV2=9mV2
The change in kinetic energy ΔK is given by:
ΔK=Kfinal−Kinitial=9mV2−mV2=8mV2
The change in kinetic energy is ΔK=8mV2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on rolling on incline plane)
28 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular momentum)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
An electron in an atom jumps in such a way that its kinetic energy changes from x to x9. The change in its potential energy (magnitude) will be-
View SolutionThe graph given below shows how the force on a mass depends on the position of the mass. What is the change in the kinetic energy of the mass as it moves from x=0.0m to x=3.0m ?

View Solution
Knowledge Check
The total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2If the speed of body is halved, what will be the change in its kinetic energy?
A1/4 timesB1/6 timesC1/8 timesD1/10 timesThe graph below shows how the force on a mass depends on the position of the mass. What is the change in the kinetic energy of the mass as it moves from x=0.0m to x=3.0 m ?
 A0.0JB20 JC50 JD60 J
A0.0JB20 JC50 JD60 J
Angular momentum of body changes by 80 kg m2/s, when its angular velocity changes from 20 rad/s to rad/s. Then the change in its kinetic energy is
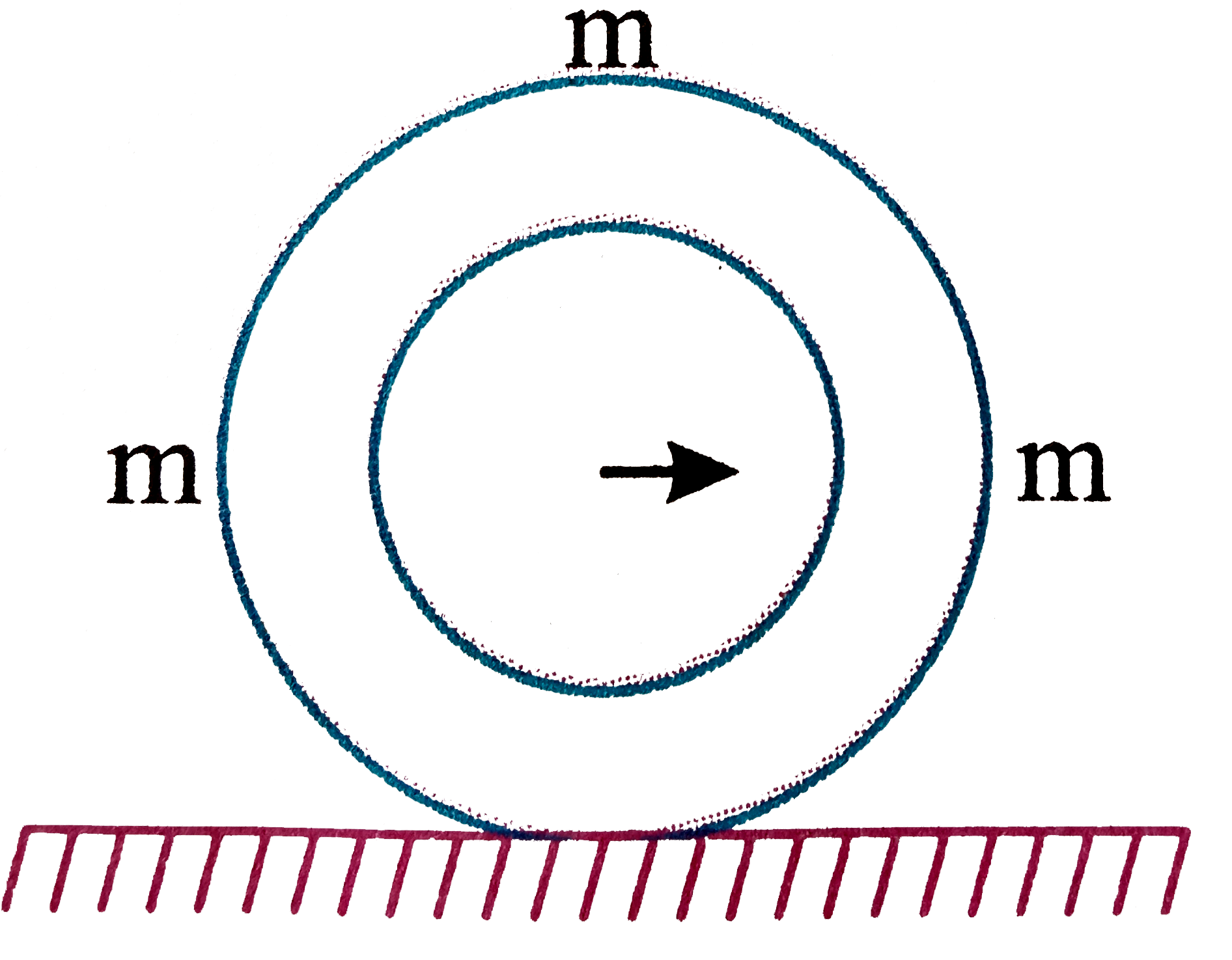
View SolutionFour beads each of mass m are glued at the top, bottom and the ends of the horizontal diameter of a ring of massm. If the ring rolls without sliding with the velocity v of its, the kinetic energy of the system (beads+ring) is
View SolutionWhen volume changes from V to 2V at constant pressure(P) then the change in internal energy will be:
View SolutionA ball of mass 1 kg carrying a charge 10−8C moves from a point A at potential 600 V to a point B at zero potential. The change in its kinetic energy is
View SolutionA thin ring of mass 1kg and radius 1m is rolling at a speed of 1ms−1. Its kinetic energy is
View Solution
