The speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by (all equation are in CGS units):
(a)The motion is uniformly accelerated along the straight line
(b)the magnitude of the acceleration at a distance 3 cm from the point is
(c)the motion is simple harmonic about the given fixed point
(d)the maximum displacement from the fixed point is 4 cm
The correct Answer is:B, C
To solve the problem, we need to analyze the given equation for the speed of a particle moving along a straight line, which is expressed as:
v2=108−9x2
Step 1: Express the speed v
From the equation, we can express the speed v as:
v=√108−9x2
Step 2: Find the acceleration a
Acceleration a can be defined as the rate of change of velocity with respect to time. We can use the chain rule to express acceleration in terms of position x:
a=vdvdt
Using the chain rule, we can express dvdt as:
dvdt=dvdx⋅dxdt=dvdx⋅v
Thus, we can rewrite acceleration as:
a=v⋅dvdx⋅v=v2⋅dvdx
Step 3: Differentiate v with respect to x
Now we need to differentiate v with respect to x:
v=3√12−x2
Differentiating v:
dvdx=3⋅12√12−x2⋅(−2x)=−3x√12−x2
Step 4: Substitute v and dvdx into the acceleration equation
Now we substitute v and dvdx into the acceleration equation:
a=v2⋅dvdx
Substituting the values:
a=(3√12−x2)2⋅(−3x√12−x2)
Calculating v2:
v2=9(12−x2)=108−9x2
Thus, we have:
a=(108−9x2)⋅(−3x√12−x2)
Step 5: Evaluate acceleration at x=3
Now, we will evaluate the acceleration at x=3:
1. Calculate v at x=3:
v=3√12−32=3√3
2. Substitute x=3 into dvdx:
dvdx=−3(3)√12−32=−9√3=−3√3
3. Substitute v and dvdx into the acceleration equation:
a=(3√3)2⋅(−3√3)=27⋅(−3√3)=−81√3
Step 6: Conclusion
The acceleration at x=3 is negative, indicating it is directed opposite to the motion. The magnitude of acceleration is:
|a|=81√3
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Comprehension
Explore 33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
The speed (v) of particle moving along a straight line, when it is of a distance (x) from a fixed point on the line, is given by : v2=144−9x2
_S01_056_Q01.png)
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
View SolutionIf the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
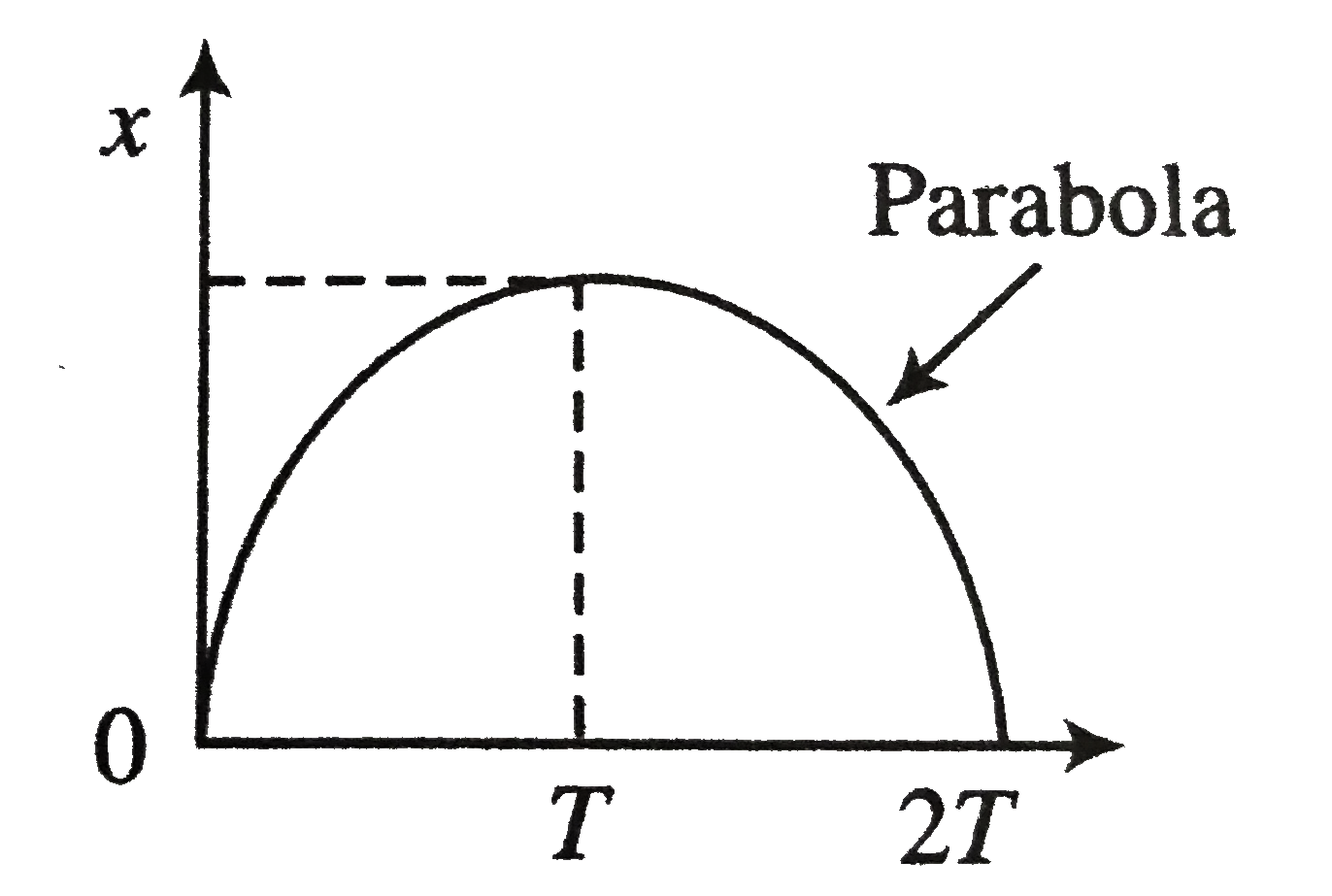
The a-t graph of the particle is correctly shown by
View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
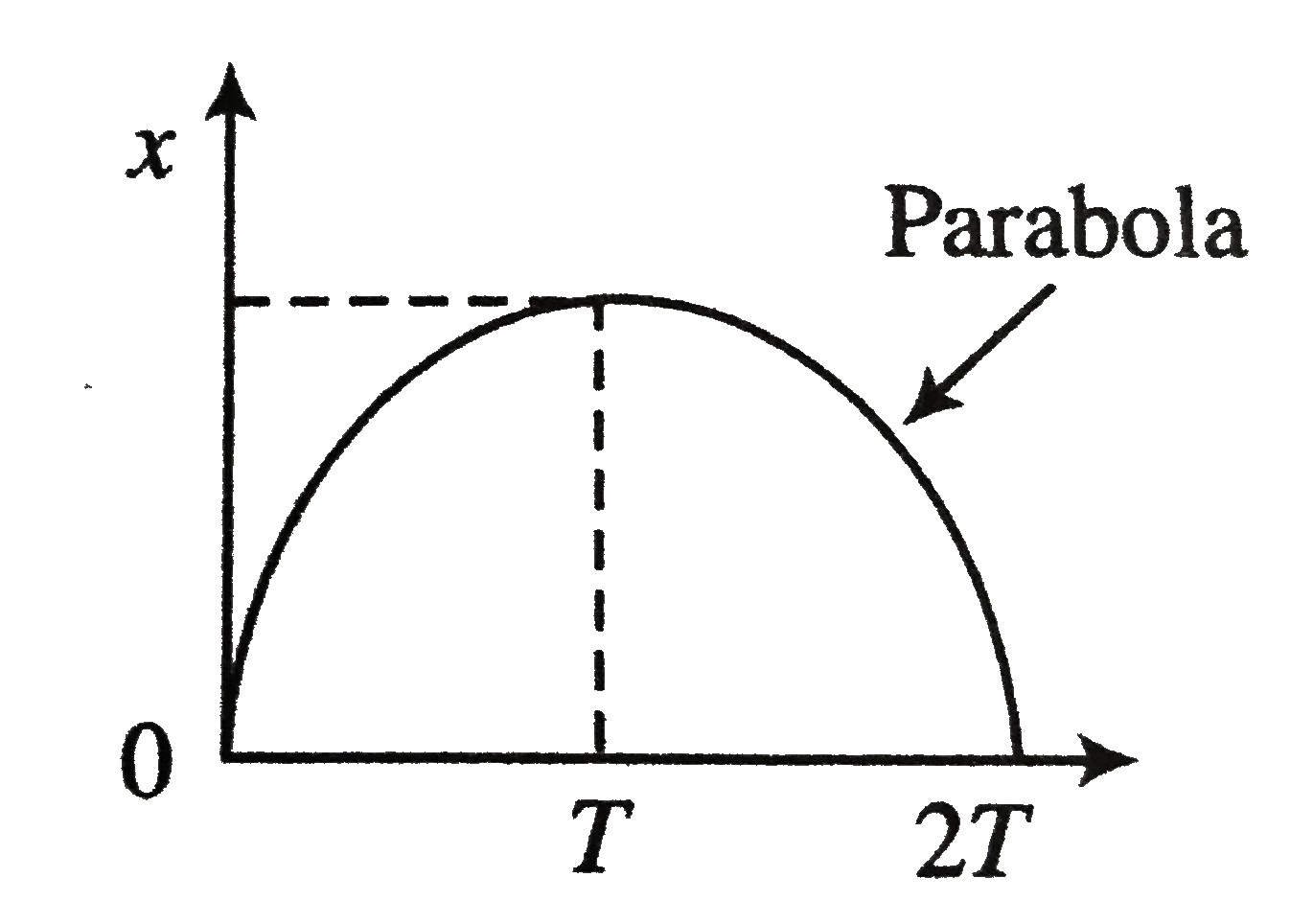
The v-t graph of the particle is correctly shown by
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View Solution
