The speed v reached by a car of mass m in travelling a distance x, driven with constant power P, is given by
(a) v=3xPm
(b) v=(3xPm)1/2
(c) v=(3xPm)1/3
(d) v=(3xPm)2
The correct Answer is:C
To solve the problem of finding the speed v reached by a car of mass m traveling a distance x while being driven with constant power P, we can follow these steps:
1. Understand the relationship between power, force, and velocity:
The power P delivered by the car can be expressed as:
P=F⋅v
where F is the force acting on the car and v is its velocity.
2. Express force in terms of mass and acceleration:
The force F can also be expressed using Newton's second law:
F=m⋅a
where a is the acceleration of the car.
3. Relate acceleration to velocity and distance:
We know that acceleration a can be expressed as:
a=dvdt=dvdx⋅v
Thus, we can rewrite the power equation as:
P=m⋅a⋅v=m⋅(dvdx⋅v)⋅v=m⋅v⋅dvdx
4. Rearranging the equation:
Rearranging the equation gives:
P=m⋅v⋅dvdx
From this, we can isolate dvdx:
dvdx=Pm⋅v
5. Integrate both sides:
We need to integrate both sides. The left side will be integrated with respect to v from 0 to v and the right side with respect to x from 0 to x:
∫v0vdv=∫x0Pmdx
6. Perform the integration:
The left side integrates to:
v22∣∣∣v0=v22
The right side integrates to:
Pm⋅x∣∣∣x0=Pm⋅x
7. Set the two integrals equal:
Thus, we have:
v22=Pm⋅x
8. Solve for v:
Multiplying both sides by 2 gives:
v2=2Pxm
Taking the square root of both sides results in:
v=√2Pxm
9. Final expression:
To express v in terms of P, x, and m:
v=√2Pxm
Final Answer:
The speed v reached by a car of mass m traveling a distance x driven with constant power P is given by:
v=√2Pxm
The power P delivered by the car can be expressed as:
P=F⋅v
where F is the force acting on the car and v is its velocity.
The force F can also be expressed using Newton's second law:
F=m⋅a
where a is the acceleration of the car.
We know that acceleration a can be expressed as:
a=dvdt=dvdx⋅v
Thus, we can rewrite the power equation as:
P=m⋅a⋅v=m⋅(dvdx⋅v)⋅v=m⋅v⋅dvdx
Rearranging the equation gives:
P=m⋅v⋅dvdx
From this, we can isolate dvdx:
dvdx=Pm⋅v
We need to integrate both sides. The left side will be integrated with respect to v from 0 to v and the right side with respect to x from 0 to x:
∫v0vdv=∫x0Pmdx
The left side integrates to:
v22∣∣∣v0=v22
The right side integrates to:
Pm⋅x∣∣∣x0=Pm⋅x
Thus, we have:
v22=Pm⋅x
Multiplying both sides by 2 gives:
v2=2Pxm
Taking the square root of both sides results in:
v=√2Pxm
To express v in terms of P, x, and m:
v=√2Pxm
The speed v reached by a car of mass m traveling a distance x driven with constant power P is given by:
v=√2Pxm
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A particle travels half of the time with constant speed 2m/s, In remaining half of the time it travels, 14th distance with constant speed of 4m/s and 34th distance with 6m/s. Find average speed during the complete journey.
View SolutionA self-propelled vehicle of mass m, whose engine delivers a constant power P, has an acceleration a=(P/mv). (Assume that there is no friction). In order to increase its velocity from v1 to v2, the distan~e it has to travel will be:
View Solution
Knowledge Check
The kinetic energy acquired by a mass m after travelling a fixed distance from rest under the action of constant force is
Adirectly proportional √mBinversely proportional to √mCdirectly proportional to m.Dindependent of m.
The speed of a car as a function of time is shown in figure.
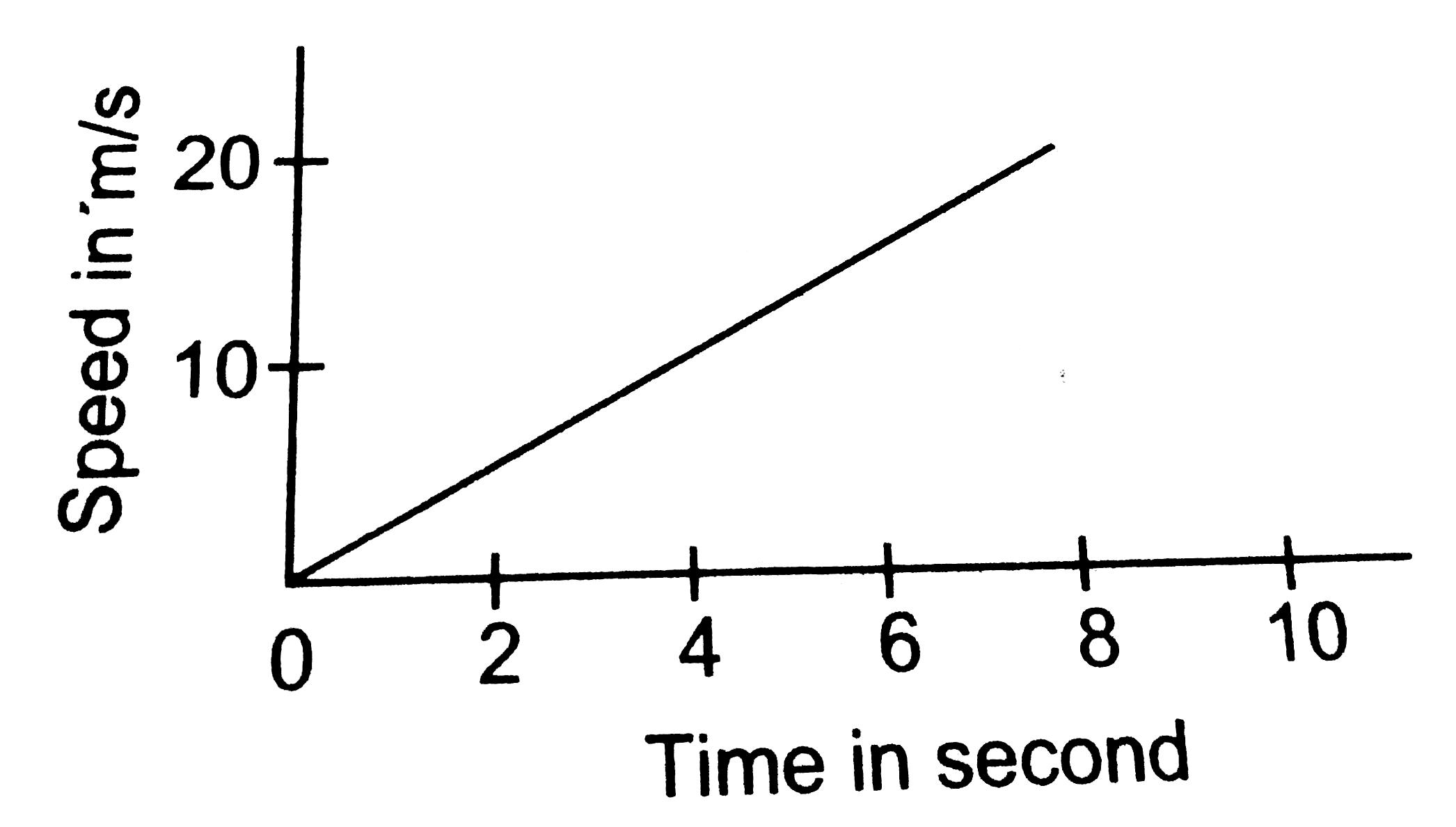
Find the distance travelled by the car in 8 seconds and its acceleration.
View SolutionA man in a car at location Q on a straight highway is moving with speed v He decides to reach a point P in a field at a distance d from the highway (point M) as shown in th e figure . Speed of the car in the field is half to that on the highway what should be the distacne RM so that the time taken to reach P is minimum ?

View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?
View SolutionA car of mass 300 kg is travelling on a circular track of radius 100 m with a constant speed of 60 m/s
Calculate the angular momentum ?
View SolutionA sphere A of mass m, travelling with speed v, collides directly with a stationary sphere B. If A is brought to rest and B is given a speed V, find (a) the mass of B (b) the coefficient of restitution between A and B?
View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionAn automobile engine propels a 1000 kg car (A) along a levelled road at a speed of 36 km//h. Find the power if the opposing frictional force is 100 N Now, suppose after travelling a distance of 200 m, this car collides with another stationary car (B) of same mass and comes to rest. Let its engine also stop at the same time. Now car (B) starts moving on the same level road without getting its engine started. Find the speed of the car (B) just after the collision.
View Solution
