The steel balls $A$ and $B$ have a mass of $500 g$ each and al rotating about the vertical axis with an angular velocity of $4 r a d / s$ at a distance of $15 C M$ from the axis. Collar $C$ is now forced down until the balls are at a distance $5 C M$ from the axis. How Much work must be done move the collar down?

Video Solution

Text Solution

Verified by Experts

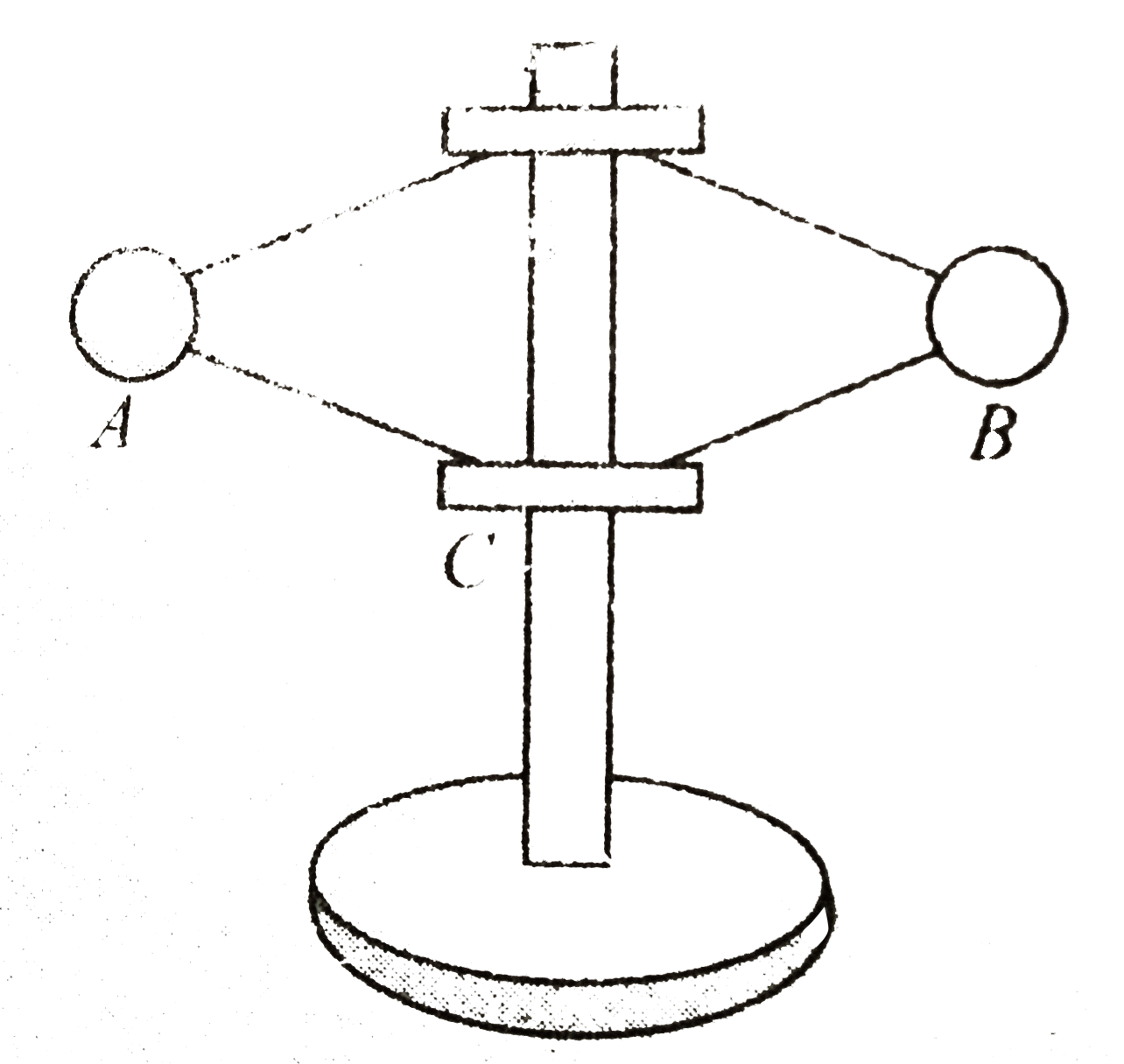
In process angular momentum remains constant
$I_{1} ω_{1} = I_{2} ω_{2}$
Where $I_{1} = 2 m {(0.15)}^{2}, ω_{1} = 4 r a d / s$
$I_{2} = 2 m {(0.05)}^{2}$
Substituting these values in above equation, we get
$ω_{2} = \frac{I_{1} ω_{1}}{I_{2}} = 36 r a d / s$
Work done on the collar
$W = \frac{1}{2} I_{2} ω_{2}^{2} - \frac{1}{2} I_{1} ω_{1}^{2}$
or $W = \frac{1}{2} {(0.05)}^{2} \times 36^{2} - \frac{1}{2} 2 m {(0.015)}^{2} \times 4^{2}$
where $m = \frac{500}{1000} = 0.05 k g = 1.44 J$

Updated on:21/07/2023