The stopping potential for photoelectrons from a metal surface is V1 when monochromatic light of frequency υ1 is incident on it. The stopping potential becomes V2 when monochromatic light of another frequency is incident on the same metal surface. If h be the Planck’s constant and e be the charge of an electron, then the frequency of light in the second case is:
υ1eh(V2+V1)
υ+eh(V1+V1)
υ1−eh(V2−V1)
υ1+eh(V2−V1)
The correct Answer is:D
According to Einstein.s photoelectric equation
eV=hυ−ϕ0
where, V = Stopoin potential
υ = Frequency of incident light
ϕ0 = Work function of metal
For the first case,
eV1=hυ1−ϕ0
For the second case,
eV2=hυ2−ϕ0
Subtract (i) from (ii), we get ....(ii)
eV2−eV1=hυ2−hυ1
e(V2−V1)=h(υ2−υ1)
eh(V2−V1)=υ2−υ1orυ2=υ1+eh(V2−V1)
Topper's Solved these Questions
- PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMBOOK - MTG-WBJEECHAPTER - PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
- OSCILLATIONS AND WAVESBOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
- SOLID STATE ELECTRONS BOOK - MTG-WBJEECHAPTER - SOLID STATE ELECTRONS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type)
15 Videos
Similar Questions
When light of wavelength λ is incident on a metal surface, stopping potential is found to be x. When light of wavelength nλ is incident on the same metal surface, stopping potential is found to be xn+1 . Find the threshold wavelength of the metal.
View SolutionWhen a metallic surface is illuminated with monochromatic light of wavelength X, the stopping potential is 5Vq. When the same surface is illuminated with light of wavelength 3X, the stopping potential is Then the work function of the metallic surface is
View Solution
Knowledge Check
Light of a particular frequency v is incident on a metal surface. When the intensity of incident radiation is increased, the photoelectric current
AdecreasesBincreasesCremains unchangedDsometimes increases and sometimes decreasesA metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
AV1+he(v1+v2)BV1+he(v2−v1)CV1+eh(v2−v1)DV1−he(v1+v2)When light of wavelength λ is incident on a metal surface ,stopping potential is found to be V∘ . When light of wavelength nλ is in incident on the same metal surface ,stopping potential is found to be V∘n+1. The threshold wavelength of the metal is
An3λBλn2Cn2λD(n+2)λ
The slope of frequency of incident light and stopping potential for a given surface will be
View SolutionMonochromatic light of frequency f1 incident on a photocell and the stopping potential is found to be V1. What is the new stopping potential of the cell if it is radiated by monochromatic light of frequency f2?
View SolutionThe stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
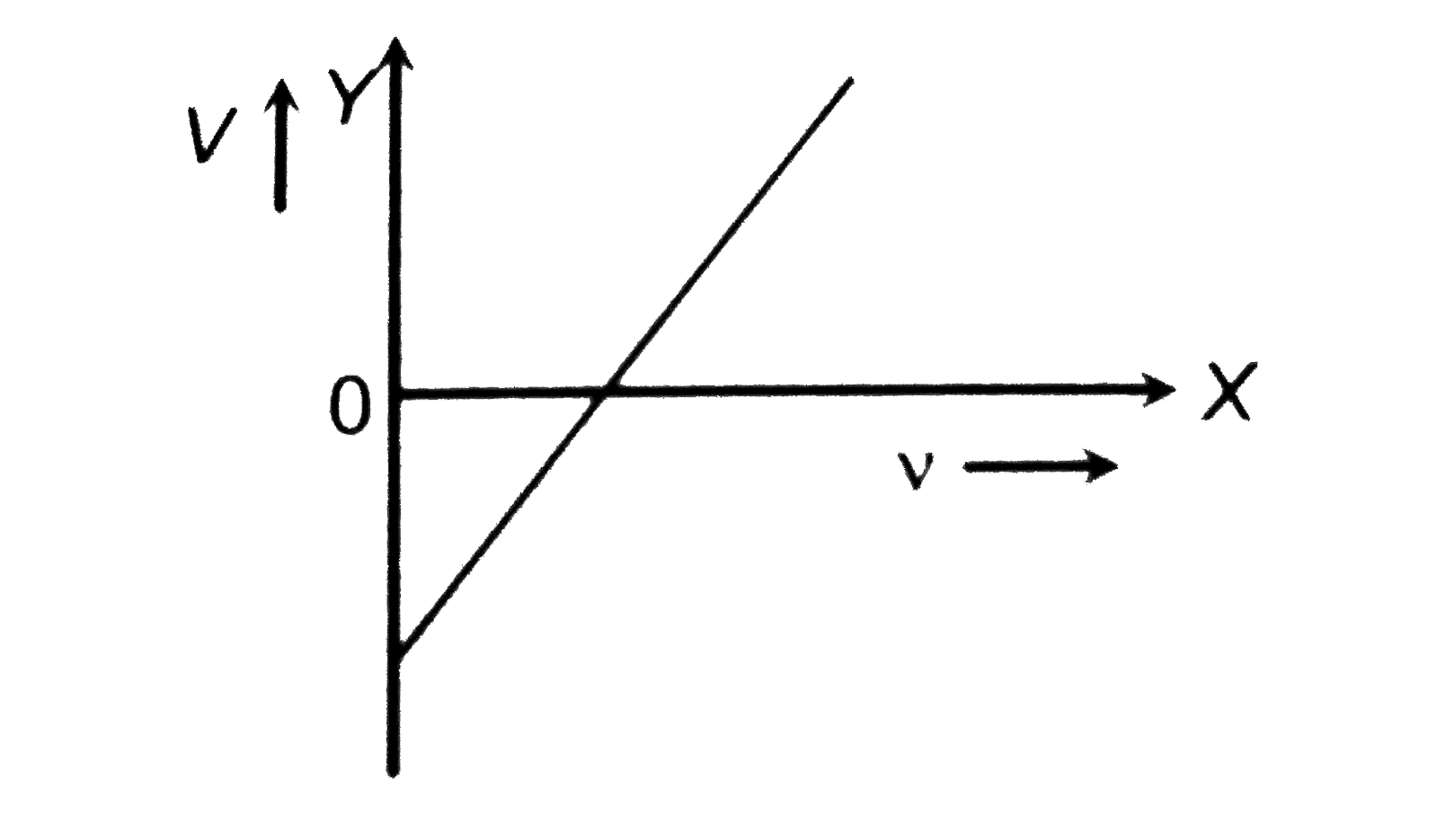
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght λ1=550nm is incident on it. The stopping potential for such electrons is λS1=0.19V. Suppose that radiation of wavelength λ2=190nm is incident of the surface.
Q. Calculate the stopping potential VS2.
View SolutionWhen light of wavelength λ is incident on photosensitive surface, the stopping potential is V. When light of wavelength 3λ is incident on same surface, the stopping potential is V6Thereshould wave length for the surface is
View Solution
