The temperature of the water of pond is 0∘C while that of the surrounding atmosphere is −20∘C. If the density of ice is p, coefficient of thermal conductivity is k and latent heat of melting is L then the thickness Z of ice layer formed increases as function of time t as
Z2=60kρLt
Z=√40kρLl
Z2=40KρL√t
z2=400kρLt
The correct Answer is:D
To find the thickness Z of the ice layer formed over time t, we can follow these steps:
Step 1: Understand the Heat Transfer
The heat current dqdt through the ice layer can be expressed using Fourier's law of heat conduction:
dqdt=kAΔTx
where:
- k is the coefficient of thermal conductivity,
- A is the area,
- ΔT is the temperature difference (which is 0−(−20)=20 °C),
- x is the thickness of the ice layer.
Step 2: Set Up the Heat Loss Equation
The heat loss dq when ice of thickness dx is formed can be expressed as:
dq=mL=ρAdxL
where:
- ρ is the density of ice,
- L is the latent heat of melting,
- m is the mass of the ice formed.
Step 3: Equate the Two Expressions
From the two expressions for dq:
ρAdxL=kA20xdt
We can cancel A from both sides:
ρdxL=k20xdt
Step 4: Rearrange and Separate Variables
Rearranging gives:
ρLdx=k20xdt
Now, we can separate the variables:
xdxρL=20kdt
Step 5: Integrate Both Sides
Integrate both sides. The left side integrates from 0 to z and the right side from 0 to t:
∫z0xdx=∫t020kρLdt
This gives:
z22=20kρLt
Step 6: Solve for z
Multiplying both sides by 2:
z2=40kρLt
Taking the square root:
z=√40kρLt
Final Expression
Thus, the thickness Z of the ice layer formed as a function of time t is:
Z=√40kρLt
The heat current dqdt through the ice layer can be expressed using Fourier's law of heat conduction:
dqdt=kAΔTx
where:
- k is the coefficient of thermal conductivity,
- A is the area,
- ΔT is the temperature difference (which is 0−(−20)=20 °C),
- x is the thickness of the ice layer.
The heat loss dq when ice of thickness dx is formed can be expressed as:
dq=mL=ρAdxL
where:
- ρ is the density of ice,
- L is the latent heat of melting,
- m is the mass of the ice formed.
From the two expressions for dq:
ρAdxL=kA20xdt
We can cancel A from both sides:
ρdxL=k20xdt
Rearranging gives:
ρLdx=k20xdt
Now, we can separate the variables:
xdxρL=20kdt
Integrate both sides. The left side integrates from 0 to z and the right side from 0 to t:
∫z0xdx=∫t020kρLdt
This gives:
z22=20kρLt
Multiplying both sides by 2:
z2=40kρLt
Taking the square root:
z=√40kρLt
Thus, the thickness Z of the ice layer formed as a function of time t is:
Z=√40kρLt
Topper's Solved these Questions
- HEAT AND THERMAL PHYSICSBOOK - MTG-WBJEECHAPTER - HEAT AND THERMAL PHYSICSEXERCISE - WB JEE WORKOUT ( CATEGORY 2: ONE OR MORE THAN ONE OPTION CORRECT TYPE)
11 Videos
- GRAVITATIONBOOK - MTG-WBJEECHAPTER - GRAVITATIONEXERCISE - WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
7 Videos
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
1 Videos
Similar Questions
Ice starts forming in a lake with water at 0∘C when the atmosphere temperature is −10∘C .If the time taken for first 1cm of ice be formed is 12 minute; the time taken for the thickness of the ice to change from 1cm to 2cm will be:
View SolutionIce has formed on a shallow pond, and a steady state has been reached, with the air above the ice at −5.0∘C and the bottom of the pond at 40∘C. If the total depth of ice + water is 1.4m, (Assume that the thermal conductivities of ice and water are 0.40 and 0.12cal/mC∘s, respectively.)
The thickness of ice layer is
View Solution
Knowledge Check
A deep rectangular pond of surface area A, containing water (density = ρ ), specific heat capacity = s), is located in a region where the outside air temperature is at a steady value of −26∘C . The thickness of the frozen ice layer in this pond, at a certain instant is x. Taking the thermal conductivity of ice as K, and its specific latent heat of fusion as L, the rate of increase of the thickness of ice layer, at this instant, would be given by
A26K/ρx(L+4s)B(26K/ρx(L−4s)C26K/(ρx2L)D26K/(ρxL)Ice starts forming in a lake with water at 0∘C when the atmospheric temperature is −10∘C. If the time taken for the first 1 cm of ice to be formed is 7 hour, then the time taken for the thickness of ice to change from 1 cm to 2 cm is
A7 hourB14 hourC21 hourD3.5 hourIf the depth of a lake is 10 m, and the temperature of surroundings is −10∘C and that of water at the bottom of the lake is 5∘C. The thermal conductivity of the Ice and water are Kf and Kw respectively. The depth of ice will be
A5KwKw+KlB10KwKw+2KlC20KlKw+2KlDNone of these
On a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is
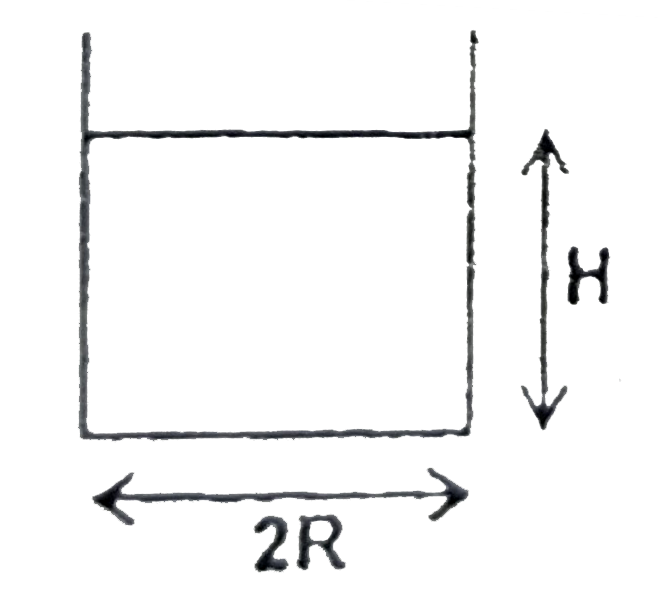
View Solution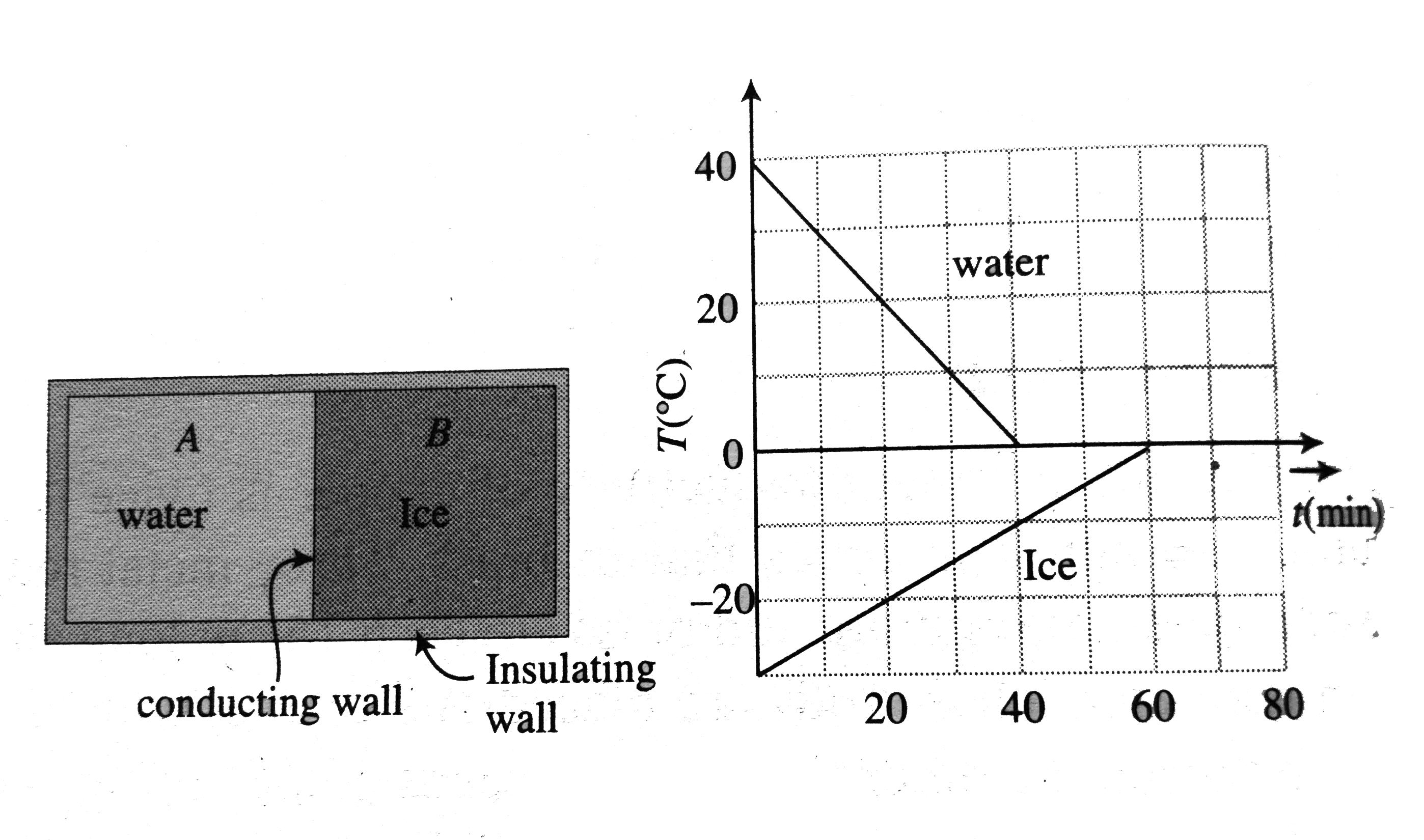
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
View SolutionIce starts forming in lake with water at 0∘C and when the atmospheric temperature is −10∘C. If the time taken for 1cm of ice be 7 hours. Find the time taken for the thickness of ice to change from 1cm to 2cm
View SolutionThe atmospheric temperature in the surroundings of a lake is -10 °C while the water in the lake is at 0 °C. If it takes 7 h to form 1 cm thick ice, then how much time is required to form another 1 cm of ice ?
View SolutionM g of ice at 0∘C is to be converted to water at 0∘C. If L is the latent heat of fusion of ice, the quantity of heat required for the above operation would be
View Solution
