The time period of a satellite is related to the density of earth (p) as
ρ12
ρ
ρ−(32)
ρ−12
To find the relationship between the time period of a satellite and the density of the Earth, we can follow these steps:
1. Understanding Kepler's Third Law:
- Kepler's Third Law states that the square of the time period T of a satellite is directly proportional to the cube of the semi-major axis r of its orbit. Mathematically, this is expressed as:
T2∝r3
2. Volume of the Earth:
- Assuming the Earth is a sphere, the volume V of the Earth can be expressed as:
V=43πr3
- This implies that the volume is also proportional to r3:
V∝r3
3. Relating Mass and Density:
- The mass M of the Earth can be expressed in terms of its volume and density ρ:
M=V⋅ρ
- Substituting the expression for volume, we have:
M=(43πr3)⋅ρ
4. Substituting Mass in Kepler's Law:
- Since the mass of the Earth is constant, we can express the relationship between T2 and ρ:
- From Kepler's law, we know T2∝r3.
- We can also express r3 in terms of density:
r3∝Mρ
- Therefore, we can write:
T2∝Mρ
5. Final Relationship:
- Rearranging the above relationship gives:
T2∝1ρ
- Taking the square root, we find:
T∝ρ−1/2
6. Conclusion:
- Thus, the time period T of a satellite is inversely proportional to the square root of the density of the Earth:
T∝1√ρ
- Kepler's Third Law states that the square of the time period T of a satellite is directly proportional to the cube of the semi-major axis r of its orbit. Mathematically, this is expressed as:
T2∝r3
- Assuming the Earth is a sphere, the volume V of the Earth can be expressed as:
V=43πr3
- This implies that the volume is also proportional to r3:
V∝r3
- The mass M of the Earth can be expressed in terms of its volume and density ρ:
M=V⋅ρ
- Substituting the expression for volume, we have:
M=(43πr3)⋅ρ
- Since the mass of the Earth is constant, we can express the relationship between T2 and ρ:
- From Kepler's law, we know T2∝r3.
- We can also express r3 in terms of density:
r3∝Mρ
- Therefore, we can write:
T2∝Mρ
- Rearranging the above relationship gives:
T2∝1ρ
- Taking the square root, we find:
T∝ρ−1/2
- Thus, the time period T of a satellite is inversely proportional to the square root of the density of the Earth:
T∝1√ρ
Topper's Solved these Questions
Similar Questions
Knowledge Check
The time period of a satellite in a circular orbit around the earth is T . The kinetic energy of the satellite is proportional to T−n . Then, n is equal to :
A12B23C43D32The time period of a geostationary satellite is
A24 hoursB12 hoursC365 daysDOne monthWhich of the following graphs is true for the motion of a satellite revolving round the Earth. ('T" is the time period of a satellite and 'r' is the distance of the satellite from the Earth).
A B
B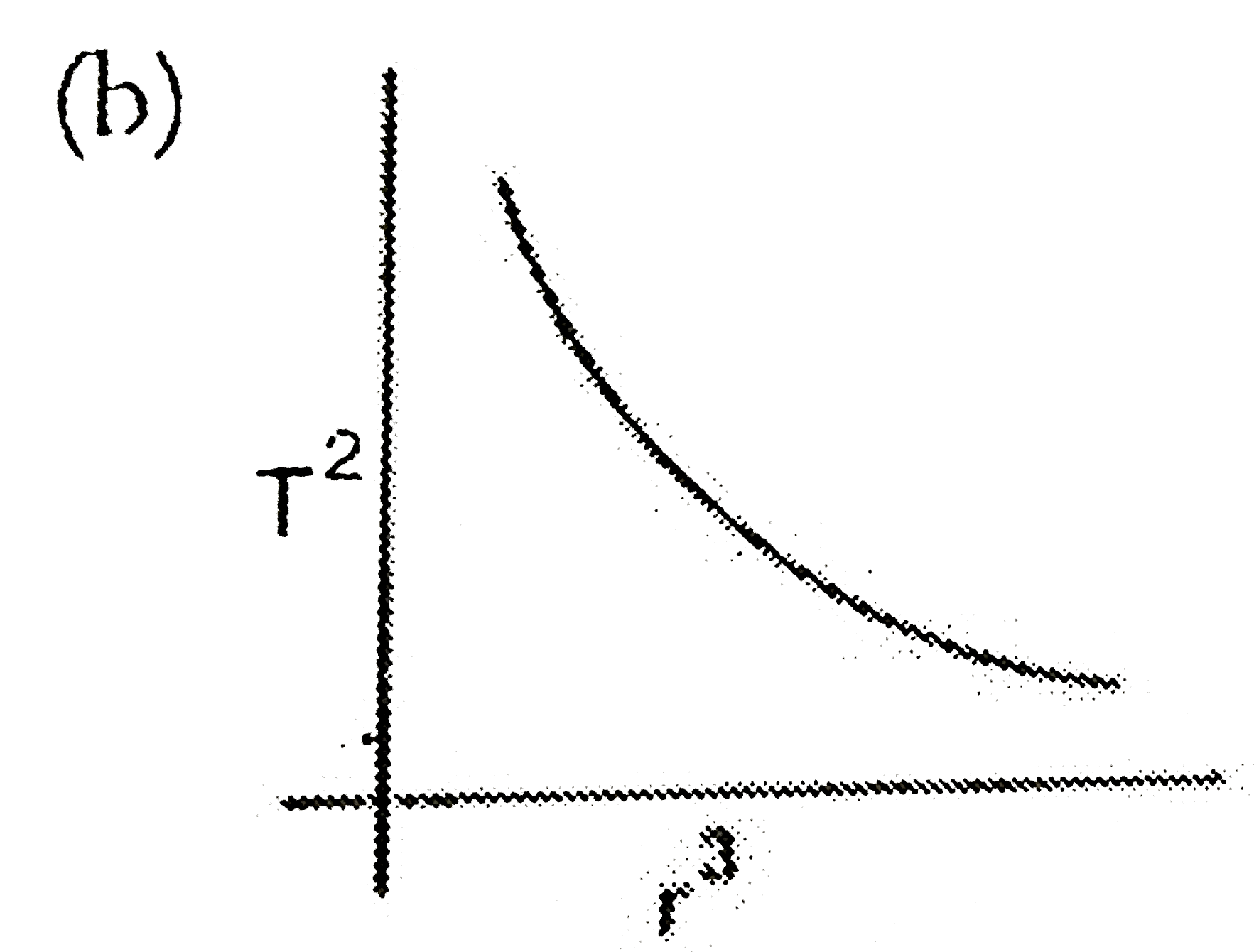 C
C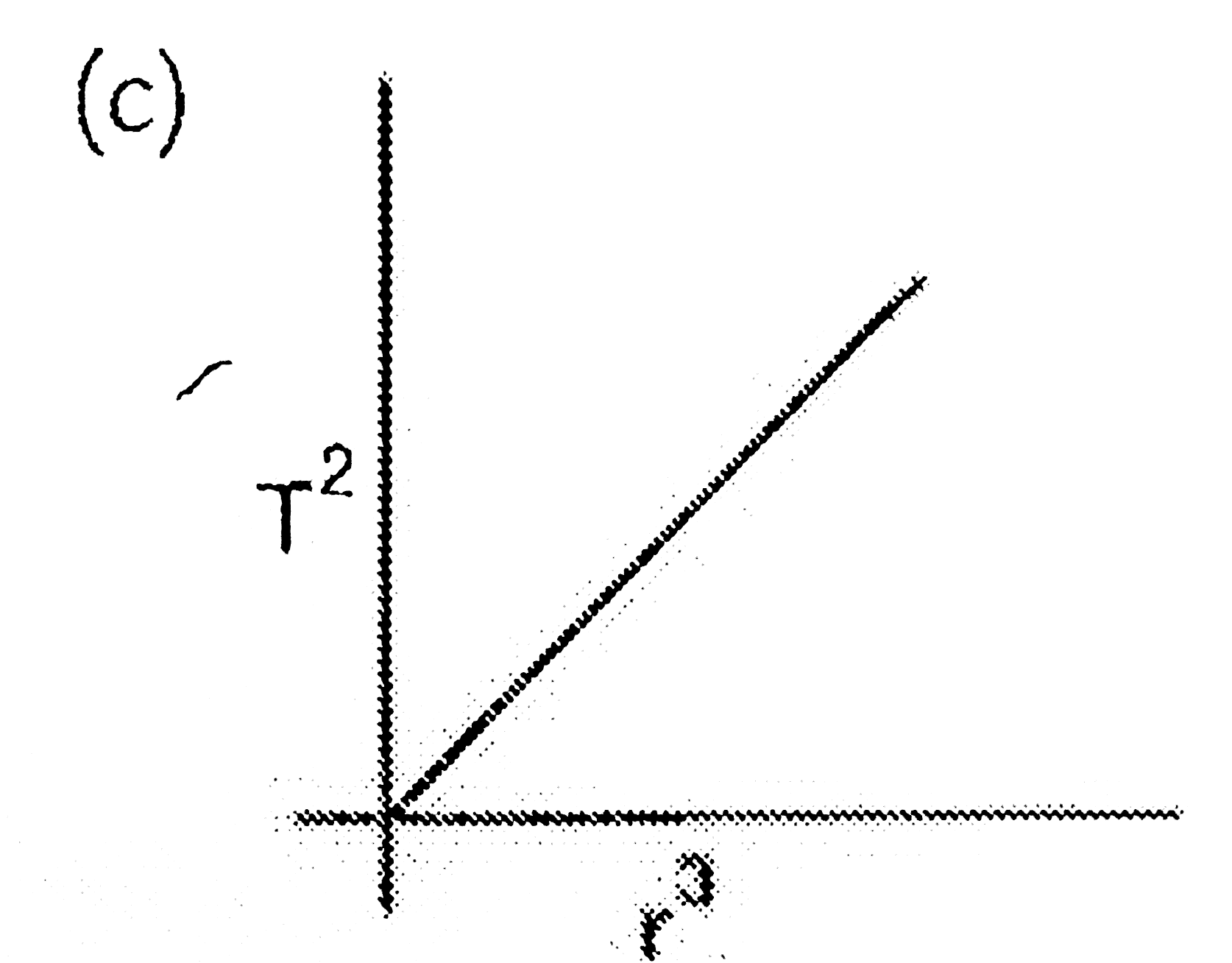 D
D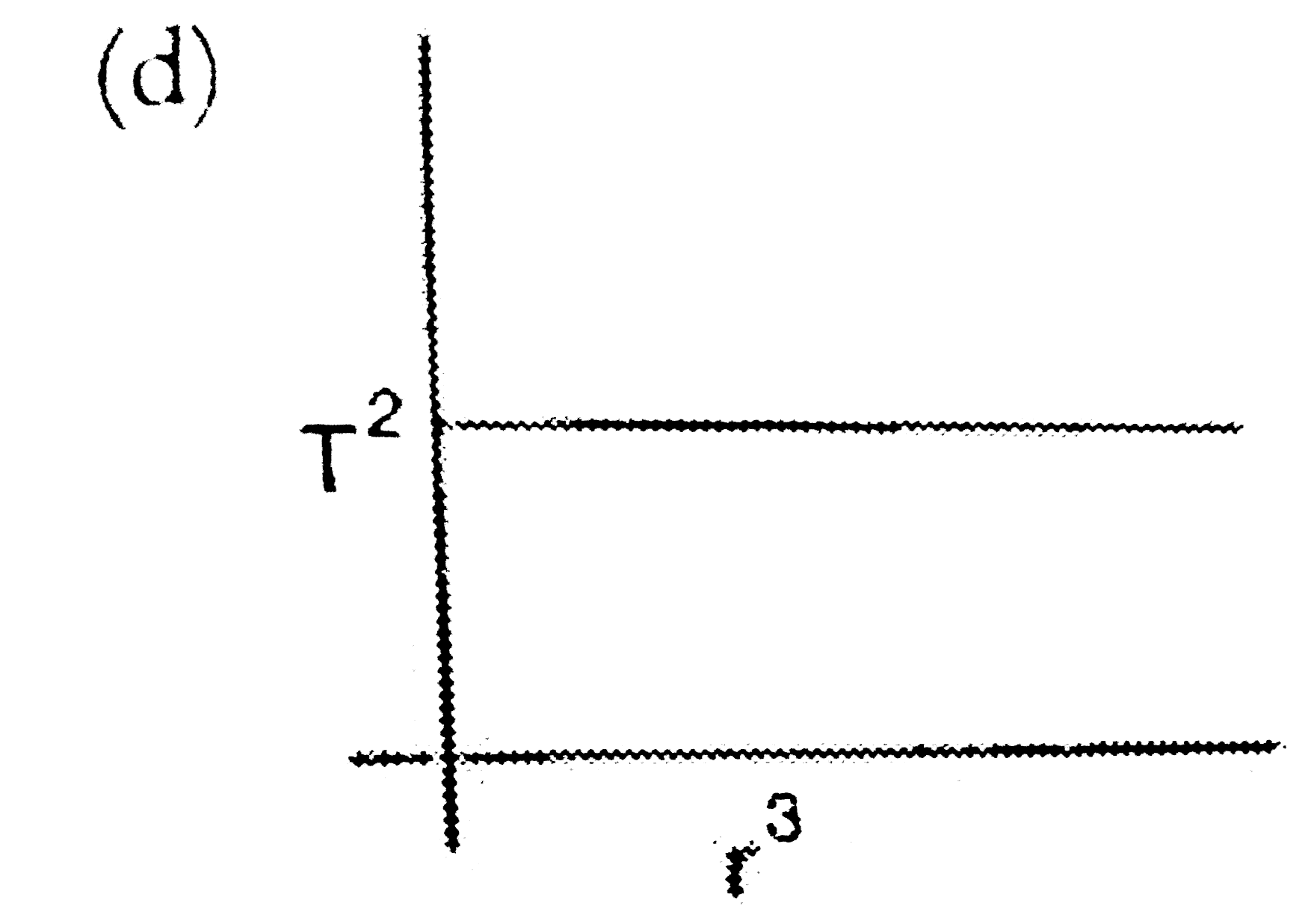
A geostationary satellite is orbiting the earth at a height of 5R above the surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R form the surface of the earth is
View SolutionThe period of revolution of an earth satellite close to surface of earth is 90min. The time period of aother satellite in an orbit at a distance of three times the radius of earth from its surface will be
View SolutionAssertion: The time period of revolution of a satellite close to surface of earth is smaller then that revolving away from surface of earth.
Reason: The square of time period of revolution of a satellite is directely proportioanl to cube of its orbital radius.
View SolutionA geostationary satellite is orbiting the earth at height 11R above surface of the earth. R being radius of earth. If the time period of this satellite is 24hr find out time period of another satellite which is revolving at 2R from surface of earth
View SolutionThe time period of a satellite of earth is 8 hours. If the separation between the earth and the satellite is increased to two times the previous value, find the new time period of the satellite.
View Solution
