The time period of an oscillating body is given by T=2π√madg. What is the force equation for this body?

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Comparing the given equation , T=2π√madg with the equation , T=2π√mk , we get k=adg. If y is the displacemetn, then force equation is
F=−ky=−adgy

Updated on:21/07/2023
|
Class 11PHYSICSSIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

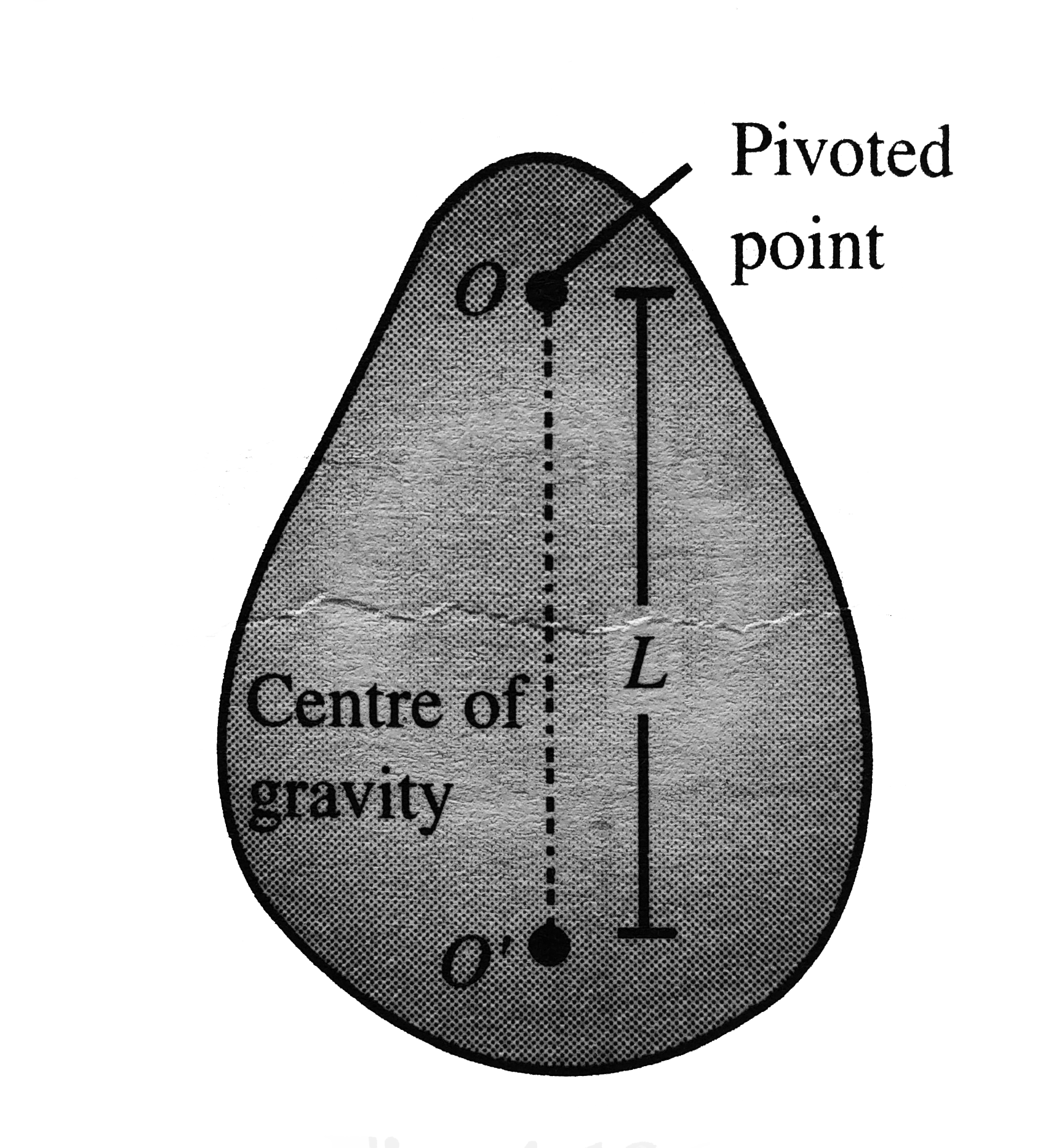
  • ocr_image
    In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
    T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
    Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
    Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
    Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.

    A2π√Lg
    Bπ√7L3g
    C2π√2l3g
    Dnone of these

  • In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
    T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
    Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
    Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
    Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
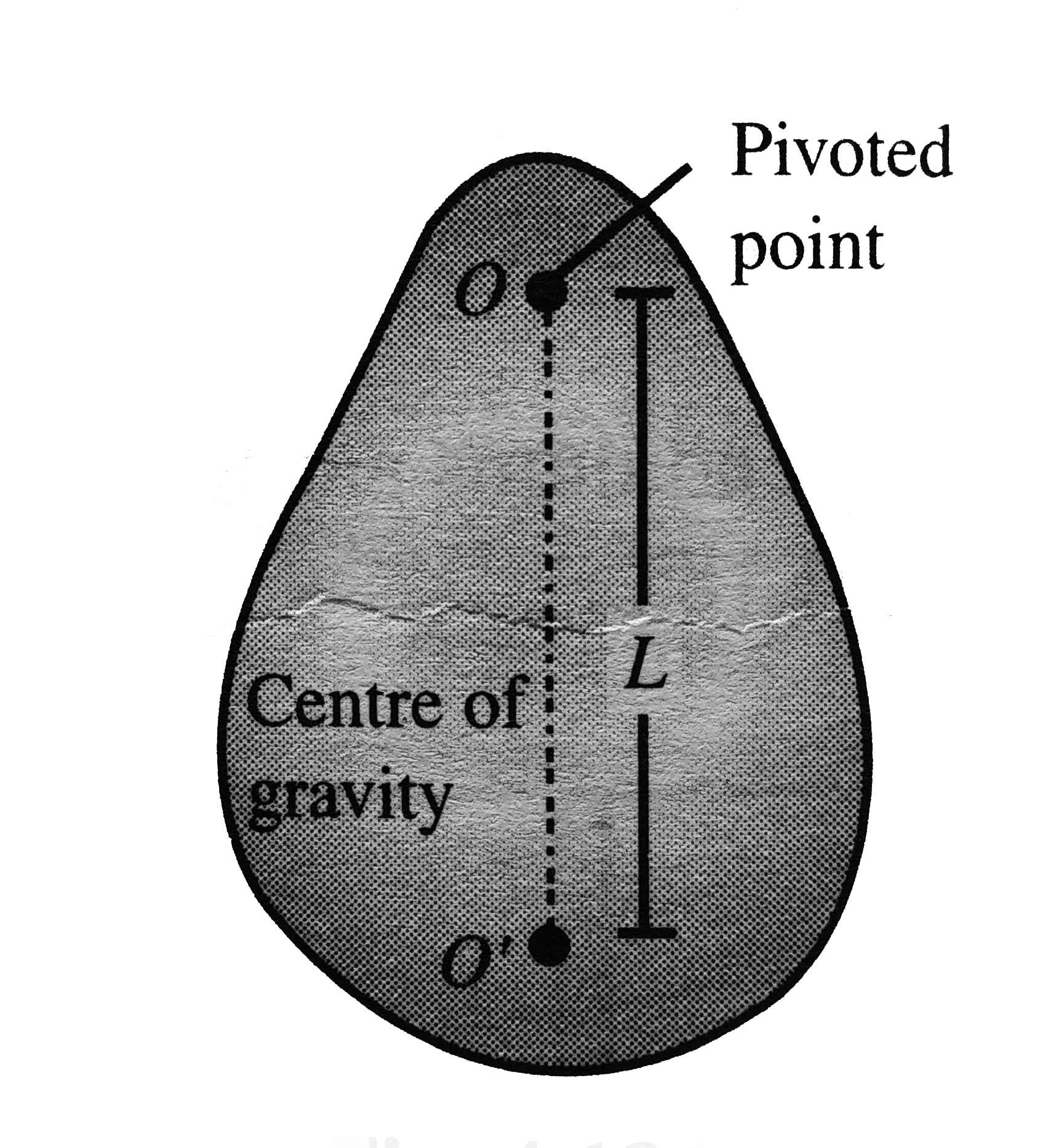    ocr_image

    A4JML
    B2JML
    C3J2ML
    DJML

  • In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
    T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
    Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
    Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
    Q. For the above question, locate the centre of oscillation.
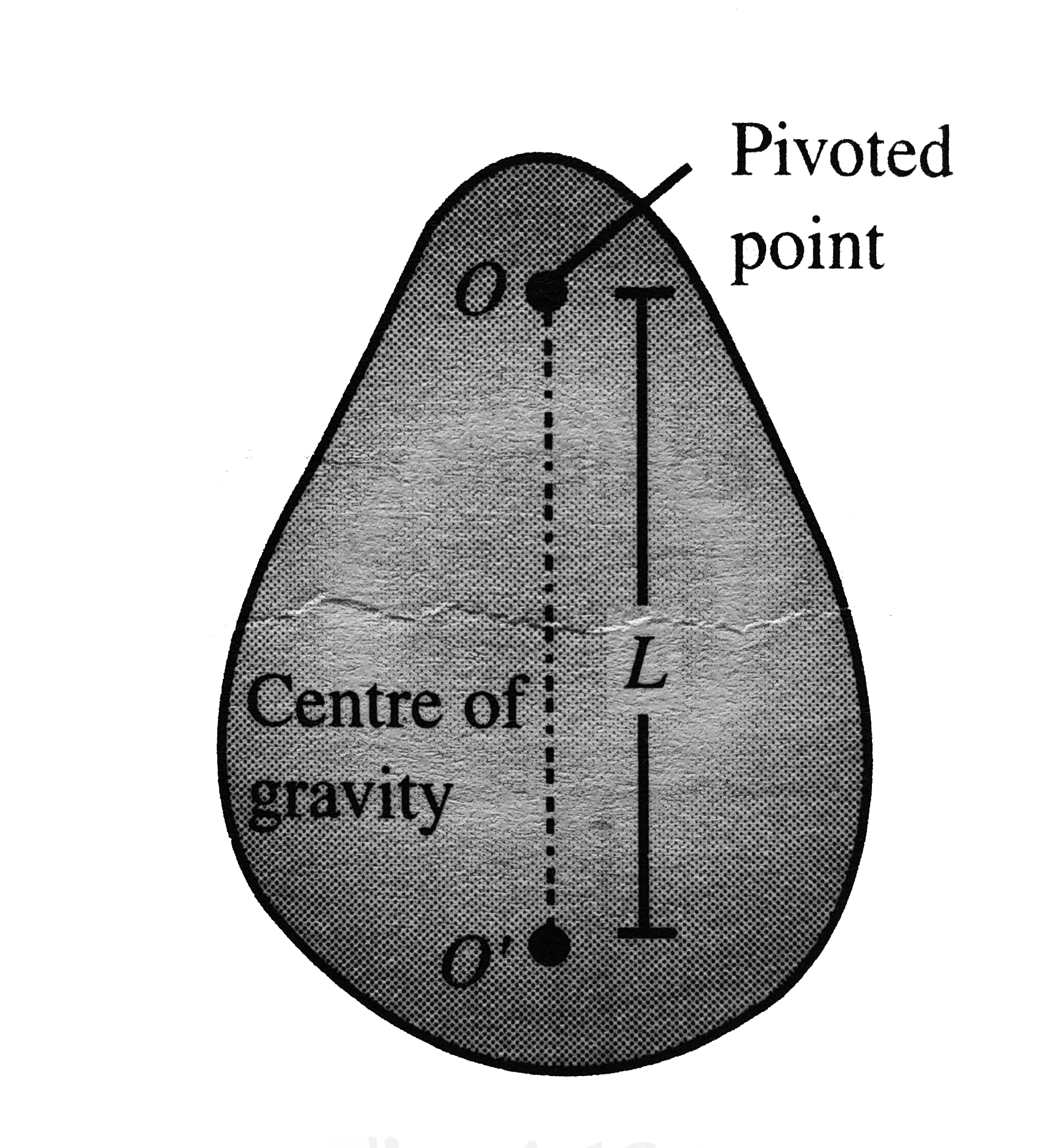    ocr_image

    AL4 from O (down)
    BL4 from O (up)
    C2L3 from O (down)
    D7L12 from O (down)