The torque τ on a body about a given point is found to be equal to A x L, where A is constant vector and L is the angular momentum of the body that point. From this, it follows that
dLdt is perpendicular to L at all instants of time.
the component of L in the direction of A does not change with time.
the magnitude of L does not change with time.
L does not change with time
The correct Answer is:A, B, C
(a,b,c) τ=vacdLdt
Given that
τ=→A×→L⇒→dLdt=→A×→L
From cross - product rule, →dLdt is always perpendicular to the
plane containing →Aand→L.
By the dot product definition
→L.→L=L2
Differentiating with respect to time
→L.d→Ldt+→L.d→Ldt=2LdLdt⇒2→L.→dLdt=2LdLdt
Since, →dLdt=0⇒dLdt=0
⇒L=constant
Thus, the magnitude of L always remains constant.
As →A is a constant vector and it is always perpendicular
to →τ,
Also, →Lisperpendica––r→→A
∴→L⊥→A∴→L.→A=0
Thus, it can be concluded that component of →Lalong→A is zero i.e., always constant.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Under a constant torque, the angular momentum of a body changes from A to 4 A in 4 sec The torque on the body will be
View SolutionA mass M hangs on a massless rod of length l which rotates at a constant angular frequency. The mass M moves with steady speed in a circuilar path of constant radius. Assume that the system is in steady circular motion with constant angular velocity ω. The angular momentum of M about point A is LA, which lies in the positive z direction and the angular momentum of M about point B is LB. The correct statement for this system is :
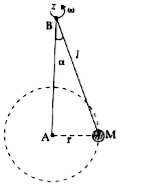
View Solution
Knowledge Check
The torque →τ on a body about a given point is found to be equal to →A and →L where →A is a constant vector, and →L is the angular momentum of the body about that point. From this it follows that
Ad→Ldt is perpendicular to →L at all instants of timeBthe component of →L in the direction of A does not change with time.Cthe magnitude of →L does not change with time.D→L does not change with time.The torque →τ on a body about a given point is found to be equal to →A×→L where →A is a constant vector and →L is the angular momentum of the body about the point. From this its follows that -
Ad→Ldt is perpendicular to →L at all instants of time.Bthe components of →L in the direction of →A does not change with time.Cthe magnitude of →L does not change with timeD→L does not change with time.Torque (→τ) acting on a rigid body is defined as →τ=→A×→L, where →A is a constant vector and →L is angular momentum of the body. The magnitude of the angular momentum of the body remains same.
→τ is perpendicular to →L and hence torque does not deliver any power to the body.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.
The angular velocity of a rigid body about any point of that body is same :
View SolutionAssertion : If there is no external torque on a body about its centre of mass, then the velocity of the centre of mass remains constant.
Reason : The linear momentum of an isolated system remains constant.
View SolutionUnder a constant torque, the angular momentum of a body changes from 2x to 5x in 8 sec. The torque acting on the body is
View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
View SolutionThe relation between the torque τ and angular momentum L of a body of moment of inertia I rotating with angular velocity ω is
View Solution
