The torque τ on a body about a given point is found to be equal to AxxL where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
dL/dt is perpendiclar to L at all instants of time
the component of L in the direction of A does not change with time
magnitude of L does not change with time
L does not change with time
The correct Answer is:A, B, C
→τ=−→dLdt
given that →τ=→A×→L
⇒−→dLdt=→A×→L
From the cross product rule −→dLdt is always perpendicular to the plane containing →A and →L. By the dot product definition. →L.→L=→L
Diferentiating with respect to time, we get
→L−→dLdt+→L−→dLdt=2L−→dLdt
−→2L−→dLdt=2LdLdt
Since −→dLdt is perpendicular to →L
dLdt=0⇒L=constant
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - LC_TYPE
8 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - SCQ_TYPE
29 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Knowledge Check
The torque τ on a body about a given point is found to be equal to A x L, where A is constant vector and L is the angular momentum of the body that point. From this, it follows that
AdLdt is perpendicular to L at all the instant of timeBthe component of L in the direction of A does not change with timeCThe magnitude of L does not change with timeDall of the aboveThe torque →τ on a body about a given point is found to be equal to →A and →L where →A is a constant vector, and →L is the angular momentum of the body about that point. From this it follows that
Ad→Ldt is perpendicular to →L at all instants of timeBthe component of →L in the direction of A does not change with time.Cthe magnitude of →L does not change with time.D→L does not change with time.The torque →τ on a body about a given point is found to be equal to →A×→L where →A is a constant vector and →L is the angular momentum of the body about the point. From this its follows that -
Ad→Ldt is perpendicular to →L at all instants of time.Bthe components of →L in the direction of →A does not change with time.Cthe magnitude of →L does not change with timeD→L does not change with time.
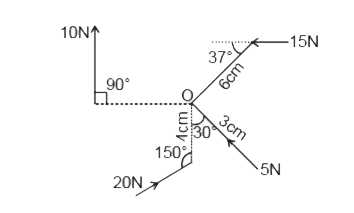
Calculate the total torque acting on the body shown in figure about the point O
View SolutionThe angular velocity of a rigid body about any point of that body is same :
View SolutionTorque (→τ) acting on a rigid body is defined as →τ=→A×→L, where →A is a constant vector and →L is angular momentum of the body. The magnitude of the angular momentum of the body remains same.
→τ is perpendicular to →L and hence torque does not deliver any power to the body.
View SolutionAssertion : If there is no external torque on a body about its centre of mass, then the velocity of the centre of mass remains constant.
Reason : The linear momentum of an isolated system remains constant.
View SolutionUnder a constant torque, the angular momentum of a body changes from 2x to 5x in 8 sec. The torque acting on the body is
View Solution
