The two batteries of emf E1 and E2 having internal resistances r1 and r2 respectively are connected in series to an external resistor R. Both the batteries are gatting discharged. The above described combination of these two batteries has to produce a weaker current then when any one of the battery is connected to same resistor. For this requirement to be fulfilled.
E2E1 must not lie between r2r1+Randr2+Rr1
E2E1 must lie between r2r1+Randr2+Rr1
E2E1 must lie between r2r1+Randr1r2+R
E2E1 must not lie between r2r1+Randr1r2+R
The correct Answer is:A
To solve the problem, we need to analyze the situation where two batteries with different EMFs (E1 and E2) and internal resistances (r1 and r2) are connected in series to an external resistor R. We want to find the condition under which the current produced by this combination is weaker than the current produced by either battery when connected individually to the same resistor R.
1. Understanding the Circuit:
- When two batteries are connected in series, the total EMF (E_total) is the sum of the individual EMFs:
Etotal=E1+E2
- The total internal resistance (R_internal) is the sum of the individual internal resistances:
Rinternal=r1+r2
2. Applying Ohm's Law:
- The total resistance in the circuit when both batteries are connected in series to the external resistor R is:
Rtotal=R+Rinternal=R+r1+r2
- The current (I_series) through the circuit can be calculated using Ohm's Law:
Iseries=EtotalRtotal=E1+E2R+r1+r2
3. Current with Individual Batteries:
- When only battery 1 is connected to the resistor R, the current (I1) is:
I1=E1R+r1
- When only battery 2 is connected to the resistor R, the current (I2) is:
I2=E2R+r2
4. Condition for Weaker Current:
- For the combination of the two batteries to produce a weaker current than either battery alone, we need:
Iseries<I1andIseries<I2
- This gives us two inequalities:
E1+E2R+r1+r2<E1R+r1
E1+E2R+r1+r2<E2R+r2
5. Simplifying the Inequalities:
- Rearranging the first inequality:
(E1+E2)(R+r1)<E1(R+r1+r2)
This simplifies to:
E2(R+r1)<E1r2
- Rearranging the second inequality:
(E1+E2)(R+r2)<E2(R+r1+r2)
This simplifies to:
E1(R+r2)<E2r1
6. Conclusion:
- The conditions derived from the inequalities provide the relationship between the EMFs and internal resistances of the batteries that must be satisfied for the combined current to be weaker than that of either battery alone.
- When two batteries are connected in series, the total EMF (E_total) is the sum of the individual EMFs:
Etotal=E1+E2
- The total internal resistance (R_internal) is the sum of the individual internal resistances:
Rinternal=r1+r2
- The total resistance in the circuit when both batteries are connected in series to the external resistor R is:
Rtotal=R+Rinternal=R+r1+r2
- The current (I_series) through the circuit can be calculated using Ohm's Law:
Iseries=EtotalRtotal=E1+E2R+r1+r2
- When only battery 1 is connected to the resistor R, the current (I1) is:
I1=E1R+r1
- When only battery 2 is connected to the resistor R, the current (I2) is:
I2=E2R+r2
- For the combination of the two batteries to produce a weaker current than either battery alone, we need:
Iseries<I1andIseries<I2
- This gives us two inequalities:
E1+E2R+r1+r2<E1R+r1
E1+E2R+r1+r2<E2R+r2
- Rearranging the first inequality:
(E1+E2)(R+r1)<E1(R+r1+r2)
This simplifies to:
E2(R+r1)<E1r2
- Rearranging the second inequality:
(E1+E2)(R+r2)<E2(R+r1+r2)
This simplifies to:
E1(R+r2)<E2r1
- The conditions derived from the inequalities provide the relationship between the EMFs and internal resistances of the batteries that must be satisfied for the combined current to be weaker than that of either battery alone.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Linked Comprehension Type Questions)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-IV LEVEL - I (MAIN) (Straight Objective Type Questions))
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-III LEVEL- I (MAIN) (Straight Objective Type Questions))
7 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Knowledge Check
Two batteries of emf e1ande2 having internal resistance r1andr2 respectively are connected in series to an external resistance R. Both the batteries are getting discharged. The above described combination of these two batteries has to produce a weaker current than when any one of the batteries is connected to the same resistor. For this requirement to be fulfilled
Aε2ε1must not lie betweenr2r1+Randr1r2+RBε2ε1must not lie betweenr2r1+Randr2+Rr1Cε2ε1must lie betweenr2r1+Randr1r2+RDε2ε1must not lie betweenr2r1+Randr2+Rr1
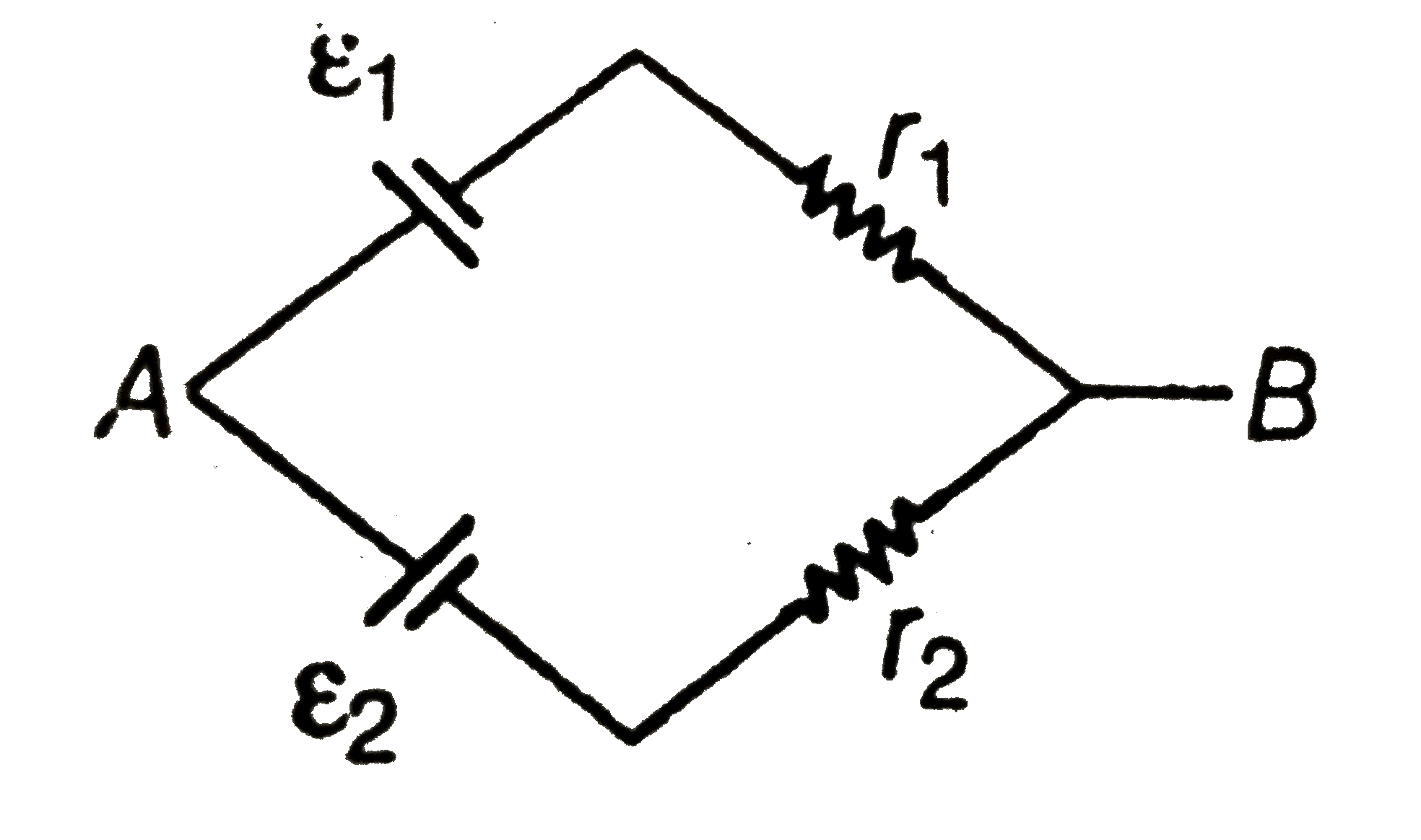
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
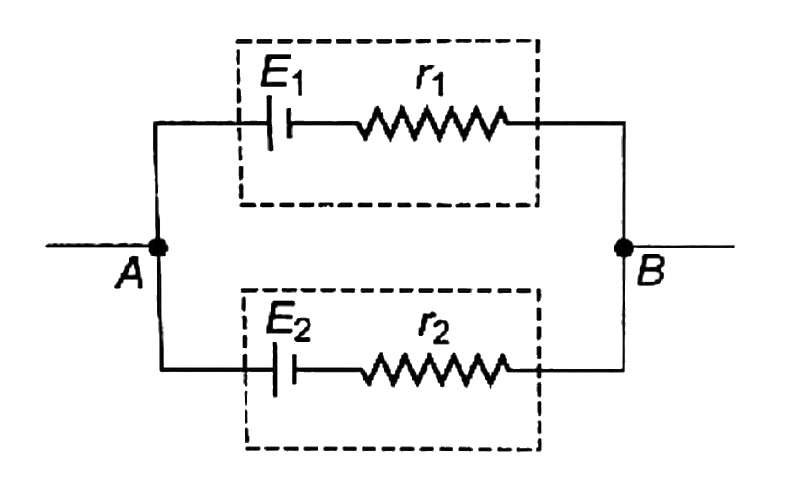
View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionTwo ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
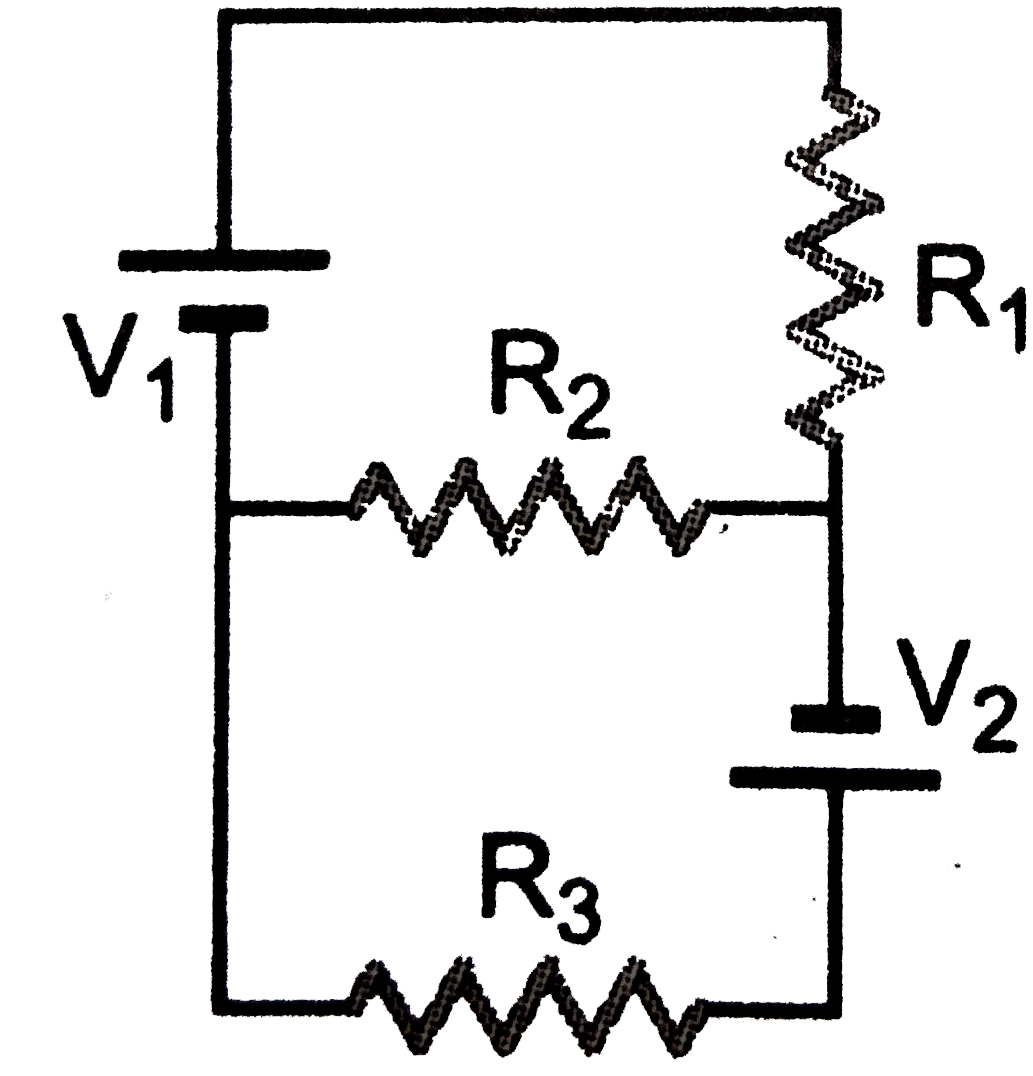
View Solution

