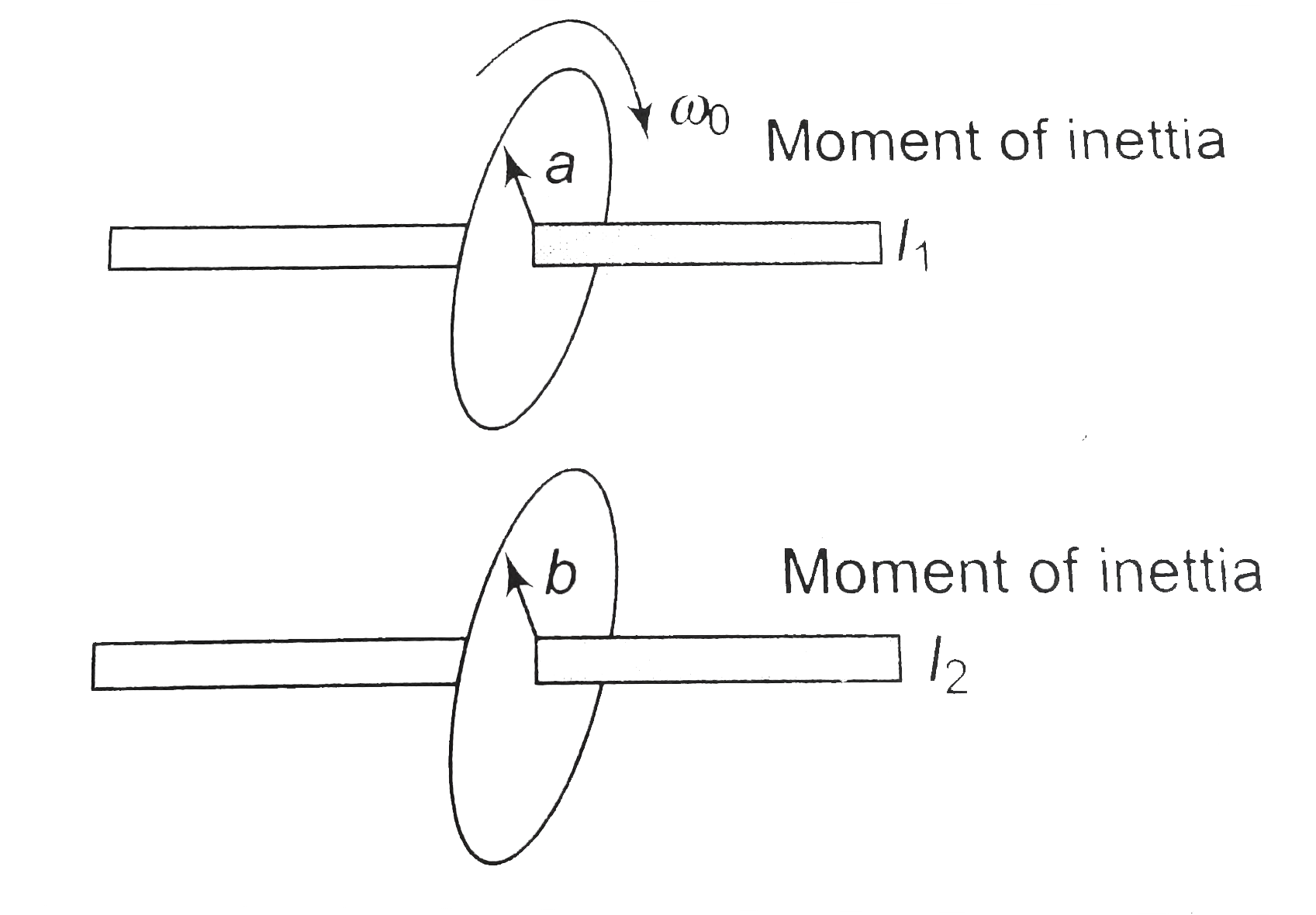
The two uniform discs rotate separately on parallel axles. The upper disc (radius $a$ and momentum of inertia $I_{1}$ ) is given an angular velocity $ω_{0}$ and the lower disc of (radius $b$ and momentum of inertia $I_{2}$ ) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is.
.

Video Solution

|

Answer

Step by step video & image solution for The two uniform discs rotate separately on parallel axles. The upper disc (radius a and momentum of inertia I_1) is given an angular velocity omega_0 and the lower disc of (radius b and momentum of inertia I_2) is at rest. Now the two discs are moved together so that their rims touch. Final angular velocity of the upper disc is. . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A disc rotates with angular velocity $ω$ and kinetic energy $E$ . Then its angular momentum
A $I ω$
B $L = \frac{E}{ω}$
C $L = \frac{2 E}{ω}$
D $L = \frac{ω}{E}$
Question 2 - Select One
A disc of moment of inertia $I_{1}$ is rotating freely with angular speed $ω_{1}$ when another non-rotating disc of moment of inertia $I_{2}$ is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
A $\frac{I_{1} ω_{1}}{I_{2}}$
B $\frac{I_{2} ω_{1}}{I_{2} + I_{2}}$
C $\frac{I_{1} ω_{2}}{I_{1} + I_{2}}$
D $\frac{(I_{1} + I_{2})}{I_{2} ω_{1}}$
Question 3 - Select One
Initial angular velocity of a circualr disc of mass M is $ω_{1} .$ The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
A $(\frac{M + m}{M}) ω_{1}$
B $(\frac{M + m}{M}) ω_{1}$
C $(\frac{M}{M + 4 m}) ω_{1}$
D $(\frac{M}{M + 2 m}) ω_{1}$

ANURAG MISHRA-RIGID BODY MOTION-MATCH THE COLUMN

Home
Ask Doubt
Profile