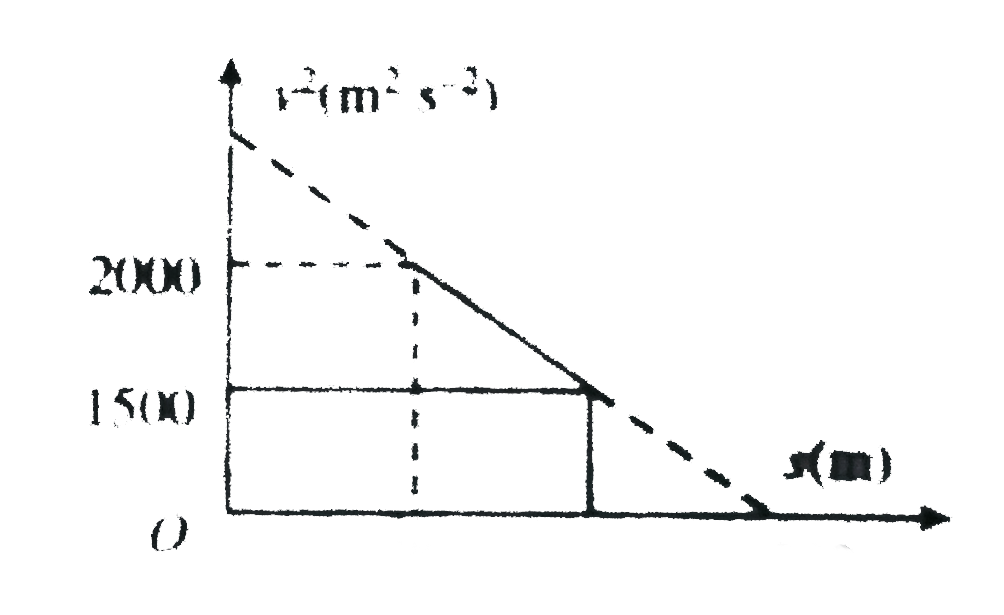
The and graph are given for two particles. Find the accelerations of the particles at .
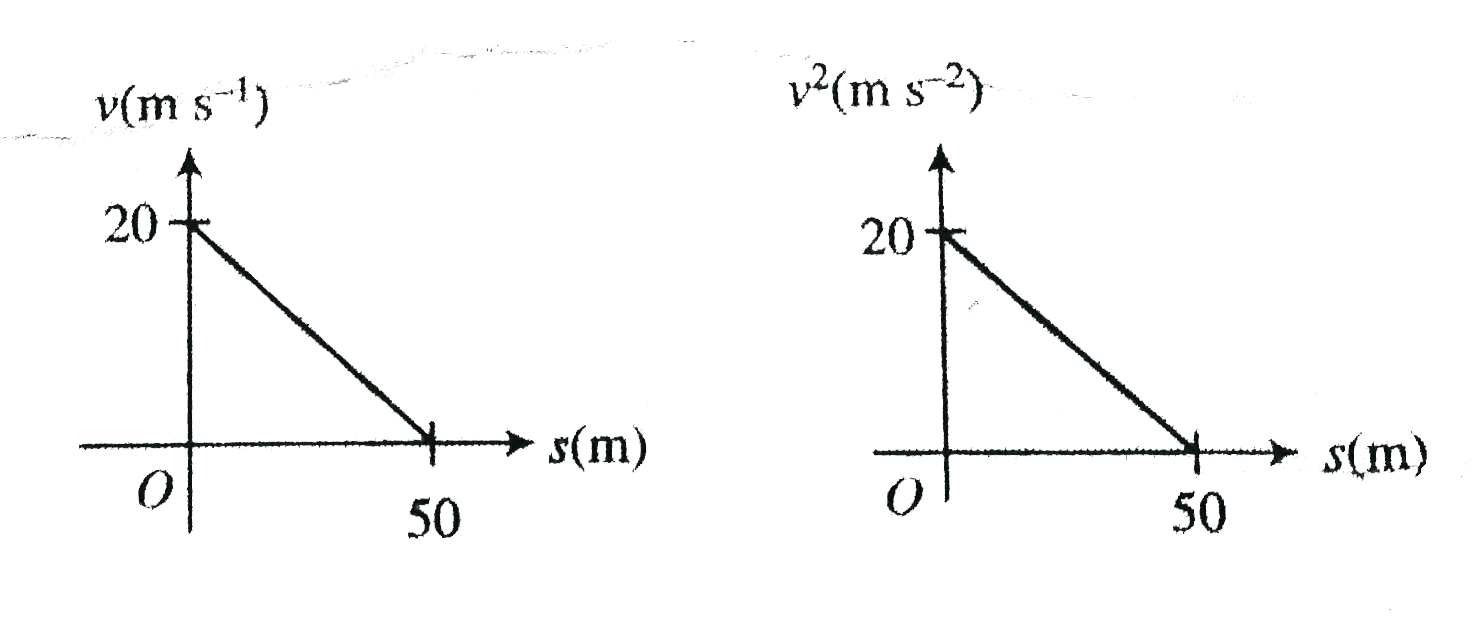 .
.
, where (at s=0)
and
Then,
, where
Then, .
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moves in a circle of radius 1.0cm with a speed given by v=2t , where v is in cm/s and t in seconds.
(a) Find the radial accerleration of the particle at t=1s .
(b) Find the tangential accerleration of the particle at t=1s .
Find the magnitude of net accerleration of the particle at t=1s .
View SolutionA particle moves in a circular path such that its speed 1v varies with distance s as v=√s, where ∝ is a positive constant. Find the acceleration of the particle after traversing a distance s.
View SolutionA particle moves in a circular path such that its speed v varies with distance as V=α√s where α is a positive constant. Find the acceleration of the particle after traversing a distance s.
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
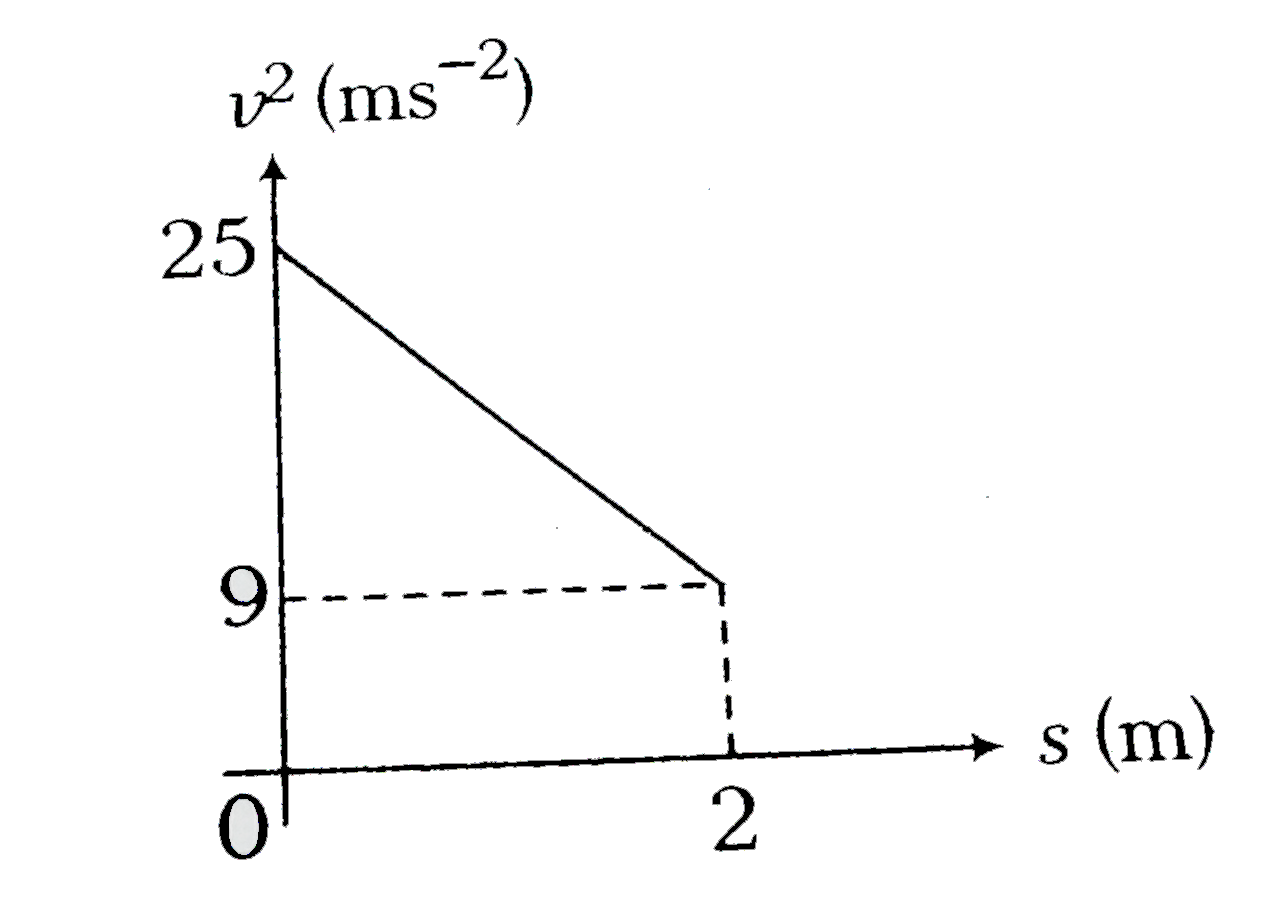
View SolutionA particle moves in circle of radius 1.0 cm at a speed given by v=2.0 t where v is in cm/s and t in seconeds. A. find the radia accelerationof the particle at t=1 s. b. Findthe tangential acceleration at t=1s. c.Find the magnitude of the aceleration at t=1s.
View SolutionA particle moves in a circular path such that its speed v varies with distance s as v=α√s where α is a positive constant. If the acceleration of the particle after traversing a distance s is [α2√x+s2R2] find x.
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View SolutionThe velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
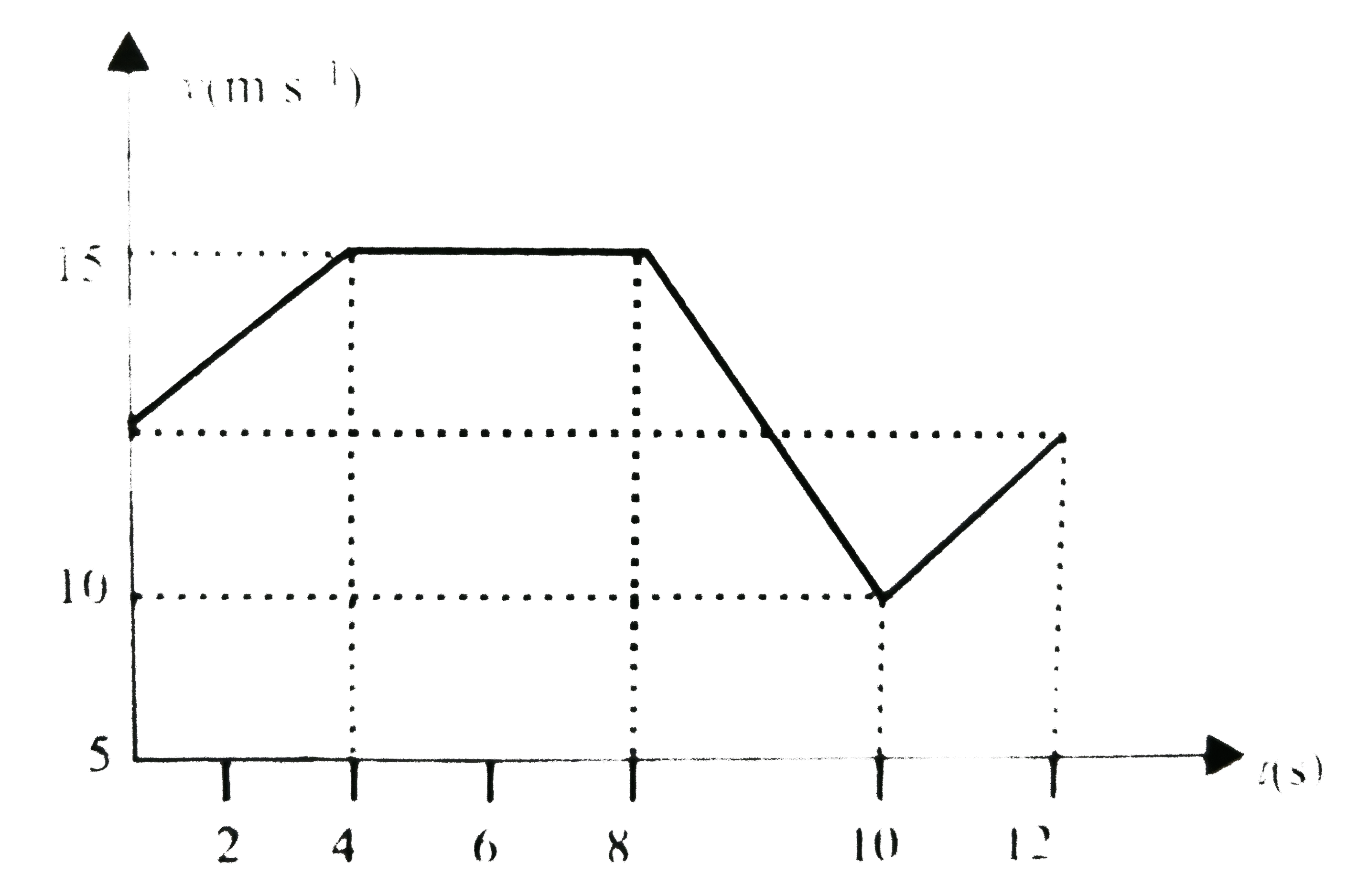 .
.
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
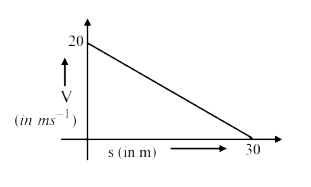
View SolutionReferrring to the v2−s diagram of a particle, find the displacement of the particle durticle during the last two seconds.
 .
.
View Solution
