The velocity of projection of oblique projectile is (6ˆi+8ˆj)ms−1 The horizontal range of the projectile is
4.9m
9.6m
19.6m
14m
Step by step video & image solution for The velocity of projection of oblique projectile is (6hati+8hatj)ms^(-1) The horizontal range of the projectile is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The initial velocity of a projectile at the point of projection is 3ˆi+4ˆj ms−1 .Then the velocity of striking on the ground is
View SolutionTwo projectiles A and B are projected with an angle of projection 15∘ for the projectile A and 45∘ for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
View Solution
Knowledge Check
The horizontal range for projectile is given by
Au2θsin2θgBu2sin2θgCu2sin2θ2gDu2cos2θgFor angle of projection of a projectile at angles and (45∘+θ), the horizontal range described by the projectile are in the ratio of
A2:1B1:1C2:3D1:2The horizontal range covered by projectile is proportional to
Aits velocityBsquare of its velocityCsine of the angle of projectionDsquare of the sine of the angle of projection
Two projectiles A and B are projected with angle of projecton 15∘ for the projectile A and 45∘ for the projectile B. If RA and RB be the horizontal range for the two projectiles then :
View SolutionFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
View SolutionFind the angle of projection of a projectile for which the horizontal range and maximum height are equal.
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
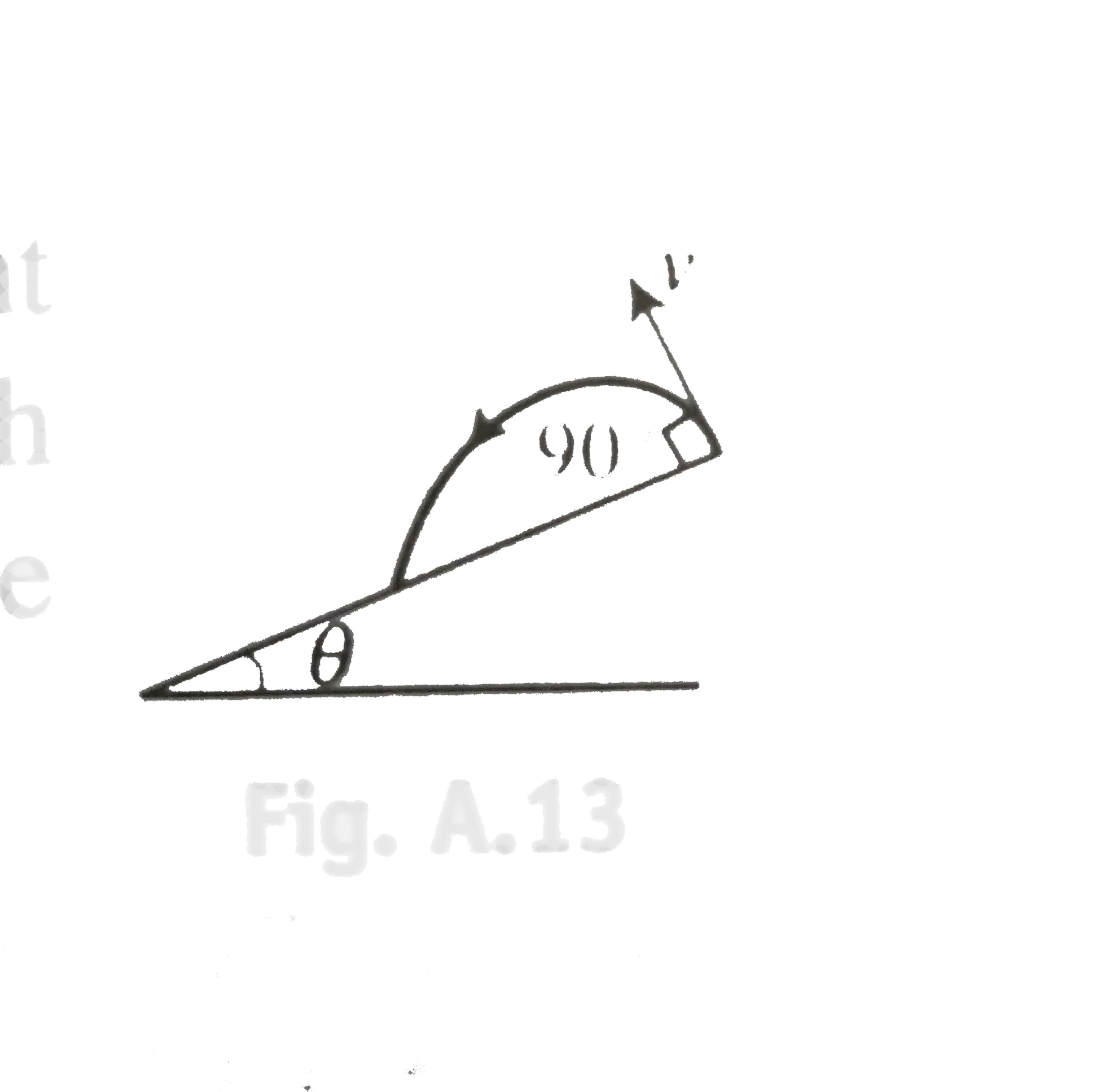
View SolutionAssertion At height 20 m from ground , velocity of a projectile is v=(20ˆi+10ˆj)ms−1. Here, ˆi is horizontal and ˆj is vertical. Then, the particle is at the same height after 4s.
Reason Maximum height of particle from ground is 40m (take, g=10ms−2)
View Solution
