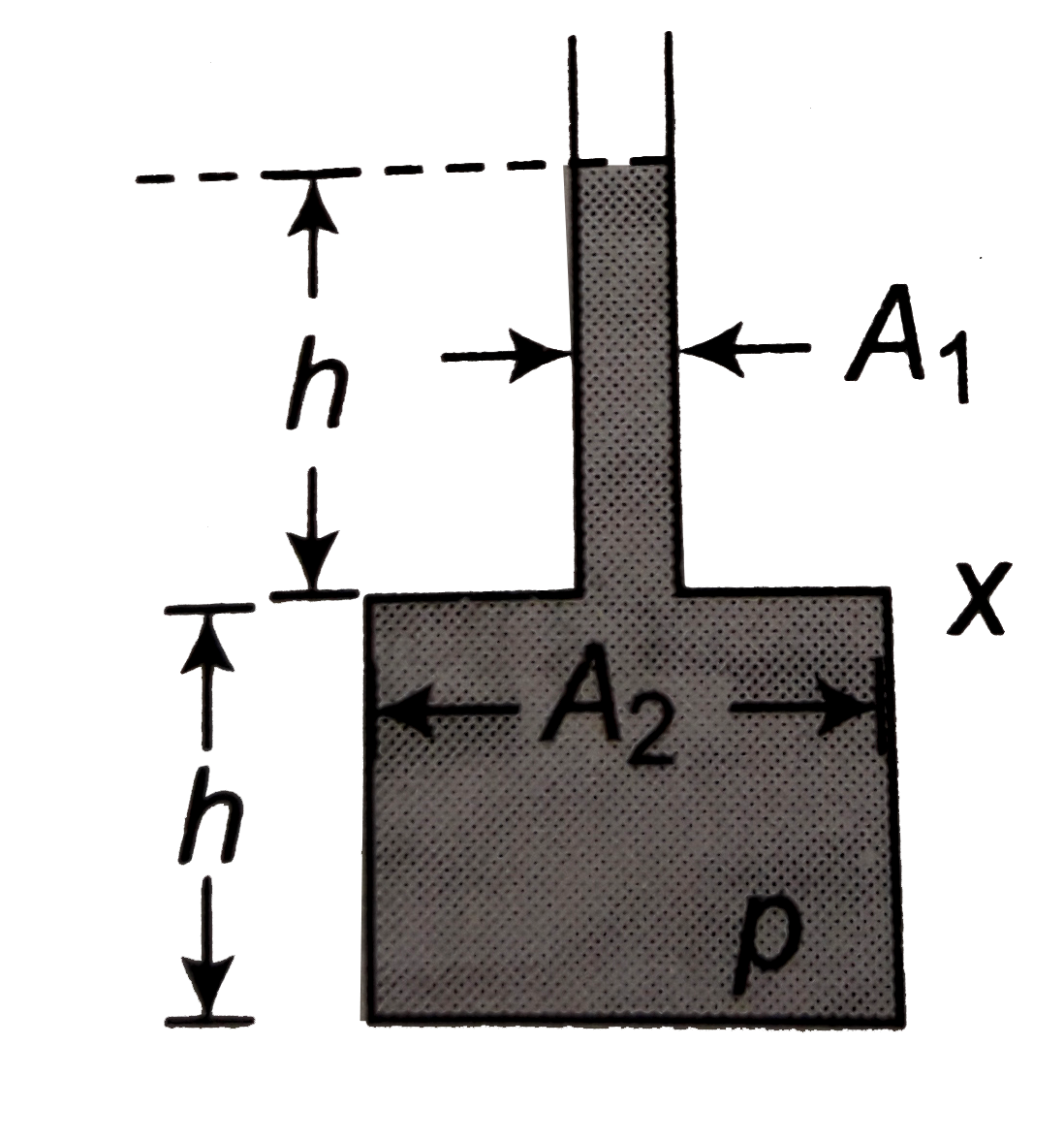
The vessel shown in the figure has a two sections of areas of cross-section A1 and A2. A liquid of density ρ fills both th sections, up to a height h in each Neglect atmospheric pressure. Choose the wrong option.
 .
.
The pressure at the base of the vessel is 2hρg.
The force exerted by the liquid on the base of the vessel is 2hρgA2.
The weight of the liquid is <2hρgA2.
The walls of the vessel at the level X exert a downward force hρg(A2−A1) on the liquid.
The correct Answer is:A, B, C, D
Step by step video, text & image solution for The vessel shown in the figure has a two sections of areas of cross-section A_1 and A_2. A liquid of density rho fills both th sections, up to a height h in each Neglect atmospheric pressure. Choose the wrong option. . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
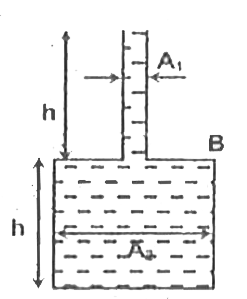
The vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
View SolutionConsider a cuboidal vessel (2R×2R×R) with as hemispherical cavity of radius R, kept at a horizontal smooth surface as shown in the figure. The vessel has very small hole of cross-sectional area "a". Now water of density ρ is poured into space developed due horizontal surface adn vessel through hole very slowly. When the height of waer level is h, the vessel lifts off the surface and liquid leaks through space generated. (R=2m,ρ=103kg/m3,m=9πkg). If the value of h is 5kcm, find the value of k.
(Atmospheric pressure =105N/m2).

View Solution
Knowledge Check

The vessel shown in the figure has two sections. The lower part is a rectangular vessel with area of cross-section A and height h. The upper part is a conical vessel of height h with base area A and top area a and the wals of the vessel are inclined at an angle 30∘ witht he vertical.A liquid of density ρ fills both the sections upto a height 2h. Neglect atmospheric pressure.AThe force F exerted by the liquid on the base of the vessel is 2hρg.(A+a)2BThe pressure P at the base of the vessel is 2hρg.AaCThe weight of the liquid W is greater than the force exerted by the liquid on the baseDthe walls of the vessel exert a downward force on the liquid.A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=ghA cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
AmρgσsBmgsCmσgρsDzero
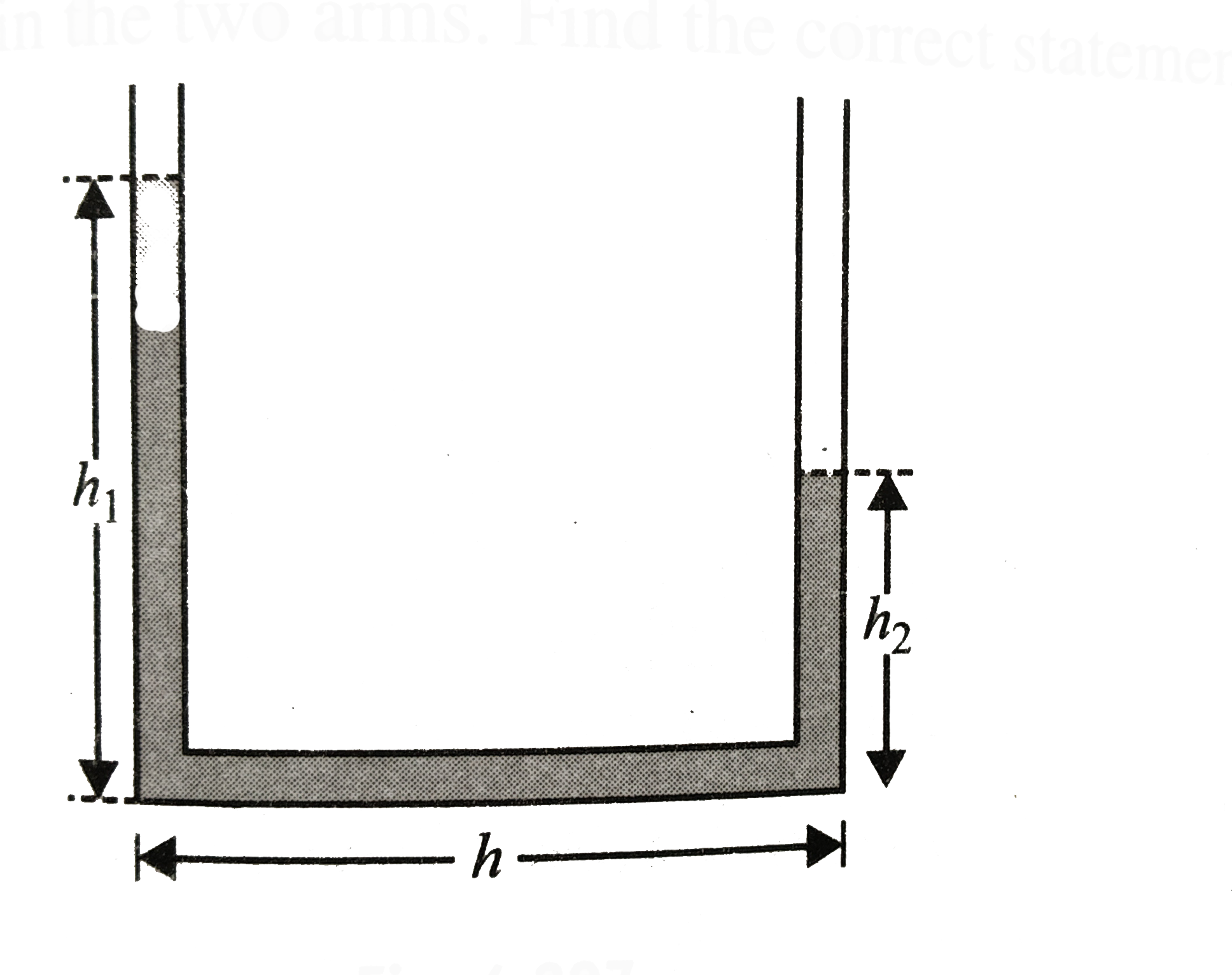
The U-tube shown in the figure has a uniform cross section. A liquid is filled up to heights h1 and h2 in the two arms and they are allowed to move. Neglecting viscosity and surface tension, find the state of the liquid when the levels equalize in the two arms. Find the correct statement.
View SolutionA fluid of density ρ flows through a horizontal pipe having two different cross-section s of areas A and 2A, Th e pressure at the smaller cross-section is P and lluid velocity at that section is v· What is the velocity and pressure at the larger cross-sect ion
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
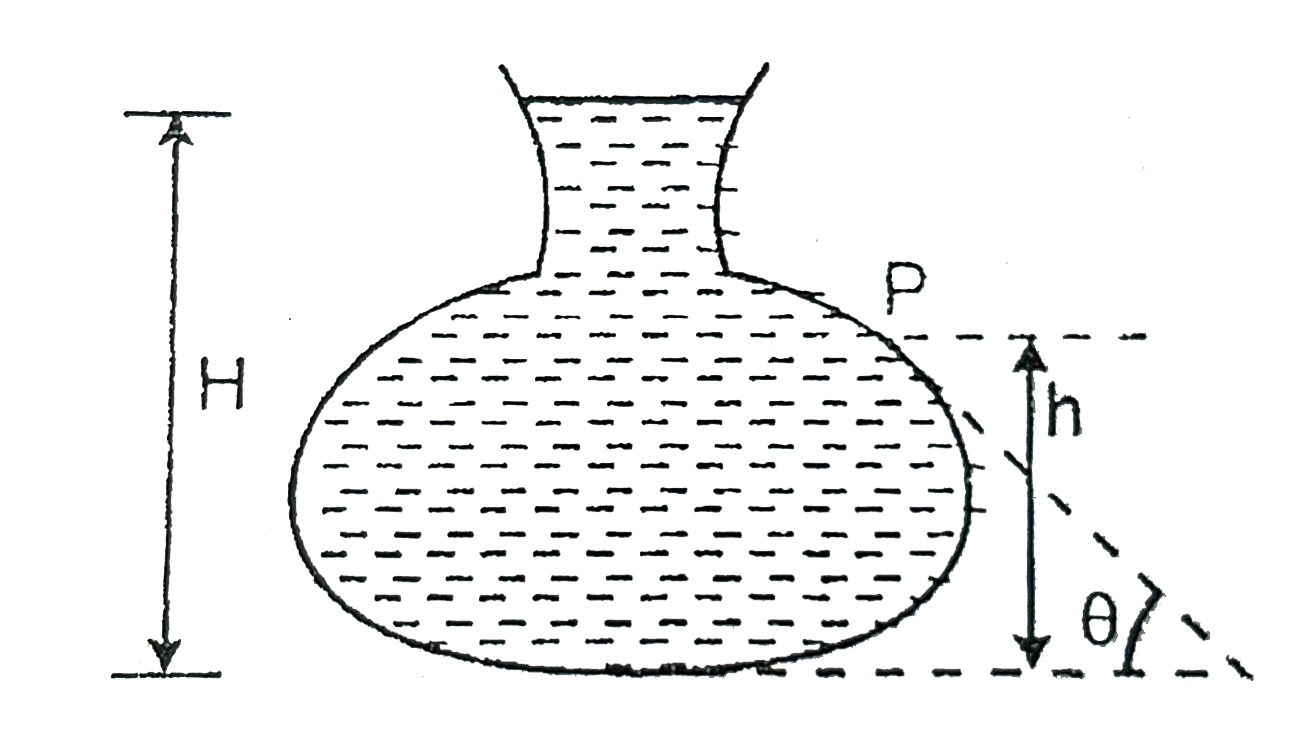
View SolutionFigure here shows the vertical cross-section of a vessel filled with a liquid of density ρ. The normal thrust per unit area on the walls vessel at point. P, as shown, will be
View SolutionA block of mass m and density p is hanging from a string . If it is lowered into a vessel of cross-sectional area A containing a liquid of density σ(<ρ) and gets fully immered, the increase in pressure at the bottom of vessel would be
View Solution
