The voltage applied to an X-ray tube is 18kV. The maximum mass of photon emitted by the X-ray tube will be
2×10−13kg
3.2×10−36kg
3.2×10−32kg
9.1×10−31kg
The correct Answer is:C
To find the maximum mass of a photon emitted by an X-ray tube when a voltage of 18 kV is applied, we can follow these steps:
Step 1: Understand the relationship between energy and mass
The energy of a photon can be related to its mass using Einstein's equation:
E=mc2
where:
- E is the energy,
- m is the mass,
- c is the speed of light in a vacuum (c≈3×108m/s).
Step 2: Determine the maximum energy of the photon
The maximum energy of the photon emitted from the X-ray tube is equal to the energy gained by an electron when it is accelerated through a potential difference V:
E=eV
where:
- e is the charge of the electron (e≈1.6×10−19C),
- V is the voltage applied (in this case, V=18kV=18×103V=1.8×104V).
Step 3: Calculate the energy of the photon
Substituting the values into the equation:
E=eV=(1.6×10−19C)(1.8×104V)
Calculating this gives:
E=2.88×10−15J
Step 4: Relate energy to mass
Now, we can relate the energy to mass using E=mc2:
m=Ec2
Substituting the values:
m=2.88×10−15J(3×108m/s)2
Step 5: Calculate the mass
Calculating c2:
c2=(3×108)2=9×1016m2/s2
Now substituting back to find m:
m=2.88×10−159×1016
m=3.2×10−32kg
Final Answer
Thus, the maximum mass of the photon emitted by the X-ray tube is:
m≈3.2×10−32kg
---
The energy of a photon can be related to its mass using Einstein's equation:
E=mc2
where:
- E is the energy,
- m is the mass,
- c is the speed of light in a vacuum (c≈3×108m/s).
The maximum energy of the photon emitted from the X-ray tube is equal to the energy gained by an electron when it is accelerated through a potential difference V:
E=eV
where:
- e is the charge of the electron (e≈1.6×10−19C),
- V is the voltage applied (in this case, V=18kV=18×103V=1.8×104V).
Substituting the values into the equation:
E=eV=(1.6×10−19C)(1.8×104V)
Calculating this gives:
E=2.88×10−15J
Now, we can relate the energy to mass using E=mc2:
m=Ec2
Substituting the values:
m=2.88×10−15J(3×108m/s)2
Calculating c2:
c2=(3×108)2=9×1016m2/s2
Now substituting back to find m:
m=2.88×10−159×1016
m=3.2×10−32kg
Thus, the maximum mass of the photon emitted by the X-ray tube is:
m≈3.2×10−32kg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct13videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Linked Comprehension62videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject17videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct10videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
Similar Questions
The voltage applied to an X-ray tube is 18 kV. The maximum mass of phton emitted by the X-ray tube will be
View SolutionThe voltage applied to an X-ray tube is 20 kV. The minimum wavelength of X-ray produced, is given by 31×n50Å then n will be
(h=6.62×10−34Jx,c=3×108m/s,e=1.6×10−19 coulomb):View SolutionA y-ray photon is emitted
View SolutionThe X-rays beam coming from an X-ray tube will be
View SolutionThe metal used for making X-ray tube window is :
View SolutionThe potential difference between the cathode. And the target electrod in a coolidge tube is 24.75 kV. The minimum wavelength of the emitted X-rays is
View SolutionAn X-ray tube is opearted at 18 kV. The maximum velocity of electron striking the target is
View SolutionA potential diffrence , the 20kv is applied across an X- ray s tube . The minimum wavelength of x- ray generated is …….Å .
View SolutionThe potential difference applied to an X-ray tube is increased. As a result, in the emitted radiation,
View SolutionFigure below shows a simple diagram of a modern X ray tube. (i.e. Coolidge tube).
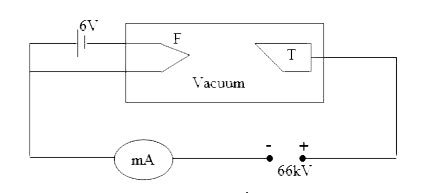
(i) Find the minimum wavelength of the X rays emitted by the X ray tube.
(ii) What will be the effect of replacing the 6V battery with a 9V battery on the emitted X rays?View Solution

