The volume of a glass vessel is 1000 cc at 20C. What volume of mercury chould be poured into it at this temperature so that the volume of the remaining space doed not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8 xx 10^(-4) o^C(-1) respectively.
Vg=1000 V_Hg=?<br>T_1 =20^0C<br>gamma_Hg= 1.8 xx 10^-4/^0C<br>gamma_g= 9 xx 10^-6/^0C<br>HereDelta Trema∈sconstant<br>Volumeofrema∈∈gspace= V'_g-V'_Hg<br>Now V'_g =V'_g(1+gamma_g Delta T)........(1)<br>V'_Hg = V_Hg (1+ gamma_Hg Delta T)........(2)<br>Subtracting (2) from (1)<br>(V'_g-V'_Hg) =(V_g- V_Hg + ((V_g) (gamma_g) Delta T))<br>-((V_Hg) (gamma_Hg) Delta T)<br>rArr V_g / V_Hg = gamma_Hg / gamma_g<br>rArr 1000 / V_Hg =(1.8 xx 10^-4)/ (9 xx 10^-6)<br>rArr V_Hg = (9 xx 10^-3)/( 1.8 xx 10^-4)= 50 cc
Topper's Solved these Questions
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
Similar Questions
A constant volume air thermometer is as shown in the figure below. Explain why the bottle is partly filled with mercury. Find the ratio fo volume of mercury present in the bottle to the volume of the bottle if the volume coefficients of mercury and glass are 1.8×10−4K−1and6×10−5K−1, respectively.
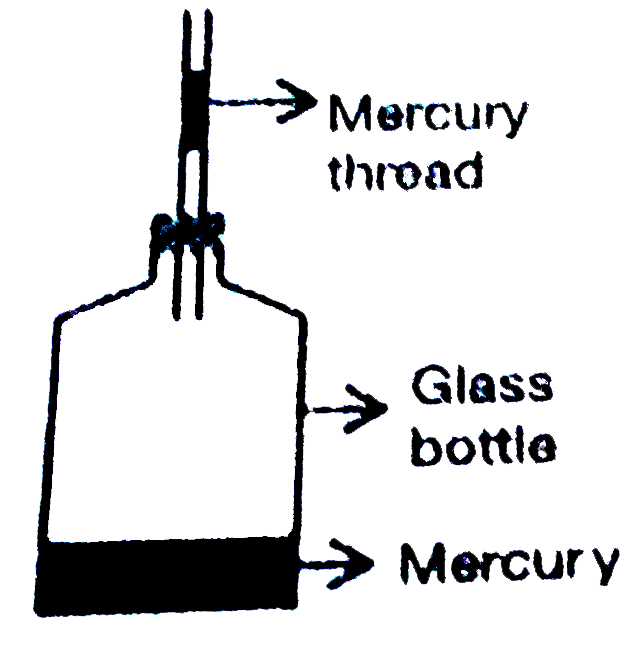
View SolutionAn iron sphere has a radius 8cm at a temperature of 0∘C. Calculate the change in volume of the sphere if is temperature is raised to 80∘C. Coefficient of liner expansion of iron =11×10−6.∘C−1.
View Solution
Knowledge Check
The remaining volume of a glass vessel is constant at all temperature if 1x of its volume is filled with mercury. The coefficient of volume expansion of mercury is 7 times that of glass. The value of x should be
A5B7C6D8A glass bulb contains air and mercury. What fraction of the bulb must be occupied by mercury if the volume of air in the bulb is to remain constant at all temperatures? The coefficient of linear expansion of glass is 9×10−6/K.
A320B32C520D12The fraction of the volume of a glass flask must be filled with mercury so that the volume of the empty space may be the same at all temperature is
(αglass=9×10−6/0C,γHg=18.9×10−5/0C)A12B17C14D15
An iron sphere has a radius of 10 cm at a temperature of 0∘C. Calculate the change in the volume of the sphere, if it is heated to 100∘C. Coefficient of linear expansion of iron =11×10−6.∘C−1.
View SolutionThe volume of a gas at STP is 273 ml. What will its volume be at a pressure of 38 cm of mercury column a and a temperature of −23∘C ?
View SolutionA glass vessel measures exactly 10cm xx 10 cm xx 10 cm at 0C. It is filled compoetely with mercury at this temperature. Whem the temperature is raised 10 10C, 1.6cm^3ofmercuryoverflows.Calca––teofl∈earexpansionofglass= 6.5 xx 10^(-6) 0^C(-1).
View SolutionIn a cylidrical glass container a solid silica is placed vertically at its bottom and remaining space is filled with mercury upto the top level of the silica. The volume of silica remains unchanged with variation in temperature. The coefficient of cubical expansion of mercury is γ and coefficient of linear expansion of glass is α. If the top surface of silica and mercury level remain at the same level wiht the variation in temperature then the ratio of volume of silica tothe volume of mercury is equal:

View SolutionA glass bulb contains air and mercury. If the volume of air in bulb is to remain constant at all temperature then the fraction of the volume of the bulb that must be occupied by mercury is x20. Find out the value of 'x' (cofficient of linear epansion of glass 9×10−6K−1, coefficient of volume expansion of mercury is 1.8×10−4K−1)
View Solution
