The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is

√332π2cm/s2
−π232cm/s2
−π232cm/s2
√332π2cm/s2
The correct Answer is:D
In general displacement of a particle performing S.H.M. is given by :
xAsin(ωt+δ) …(i)
Here in this case particle at t = 0 is crossing origin in positive direction hence δ=0.
time period of motion : T= 8s
ω=2πT=2π8=π4
Substituting in equation (i) we get
x=Asin(π4t)
Here amplitude A = 1 cm
⇒x=sin(π4t) , where x is measured in cm.
⇒dxdt=π4cos(π4t)
⇒a=d2xdt2=π216sin(π4t)
Substituting t = 4/3 s
a=−π216sin(π4×43)=−π216sin(π/3)
⇒=−π2√332cm/s2
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question)
11 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question) based on a given passage/comprehension
9 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition file (Multiple choice question) JEE (Main) & Other State Boards for Engineering Entrance
25 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Knowledge Check
The x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
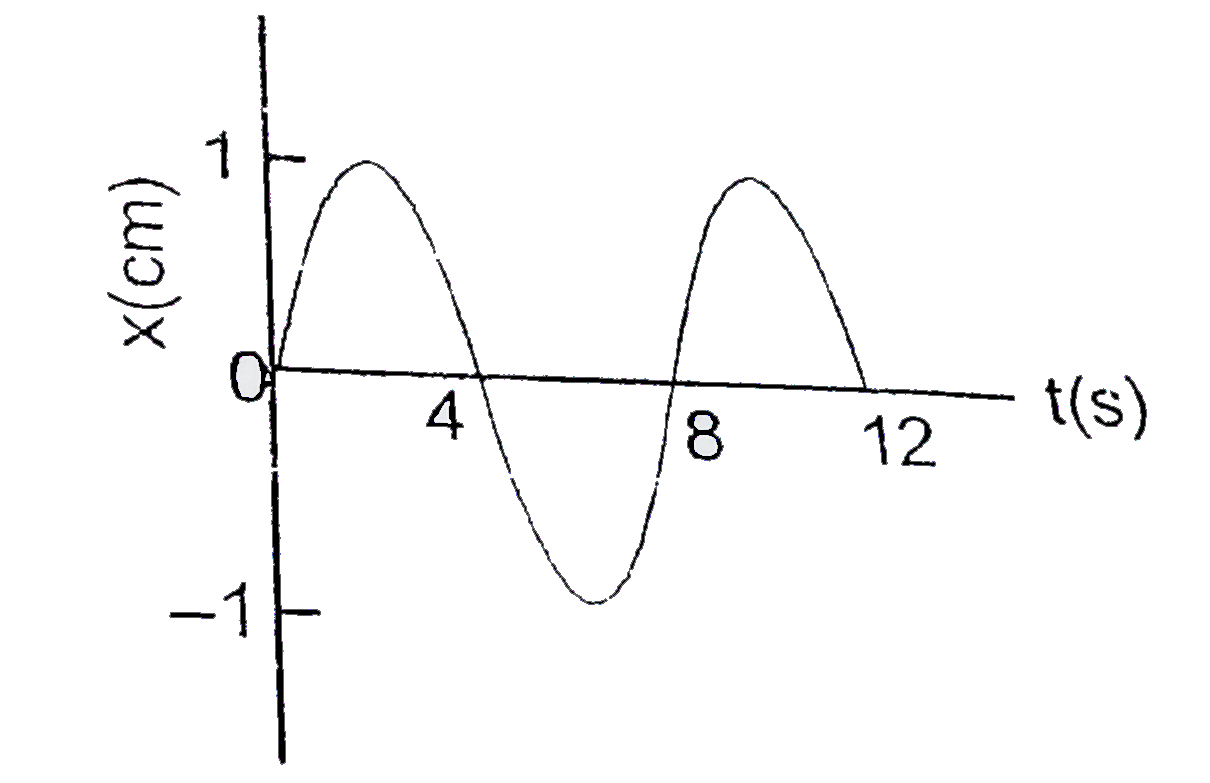 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
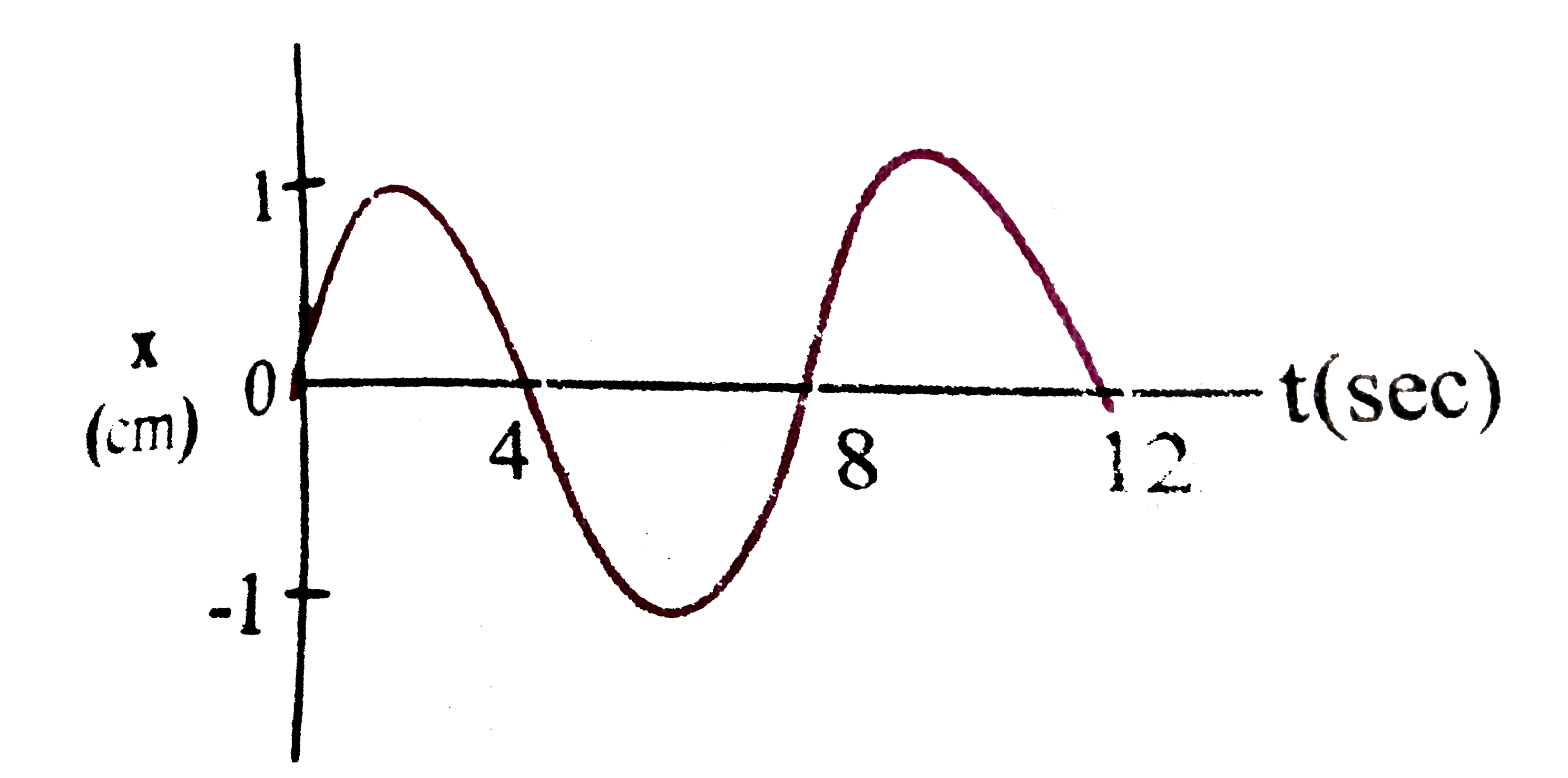 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2The x-t graph of a particle undergoing SHM is as shown in figure. The acceleration of the particle at t=2/3 is
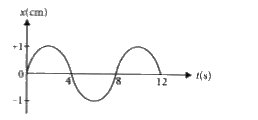 A√332π2cms−2B−π232cms−2Cπ232cms−2D−√332π2cms−2
A√332π2cms−2B−π232cms−2Cπ232cms−2D−√332π2cms−2
The velovity-time graph of a particle moving in a straitht line is shown in . The acceleration of the particle at t=9s is.
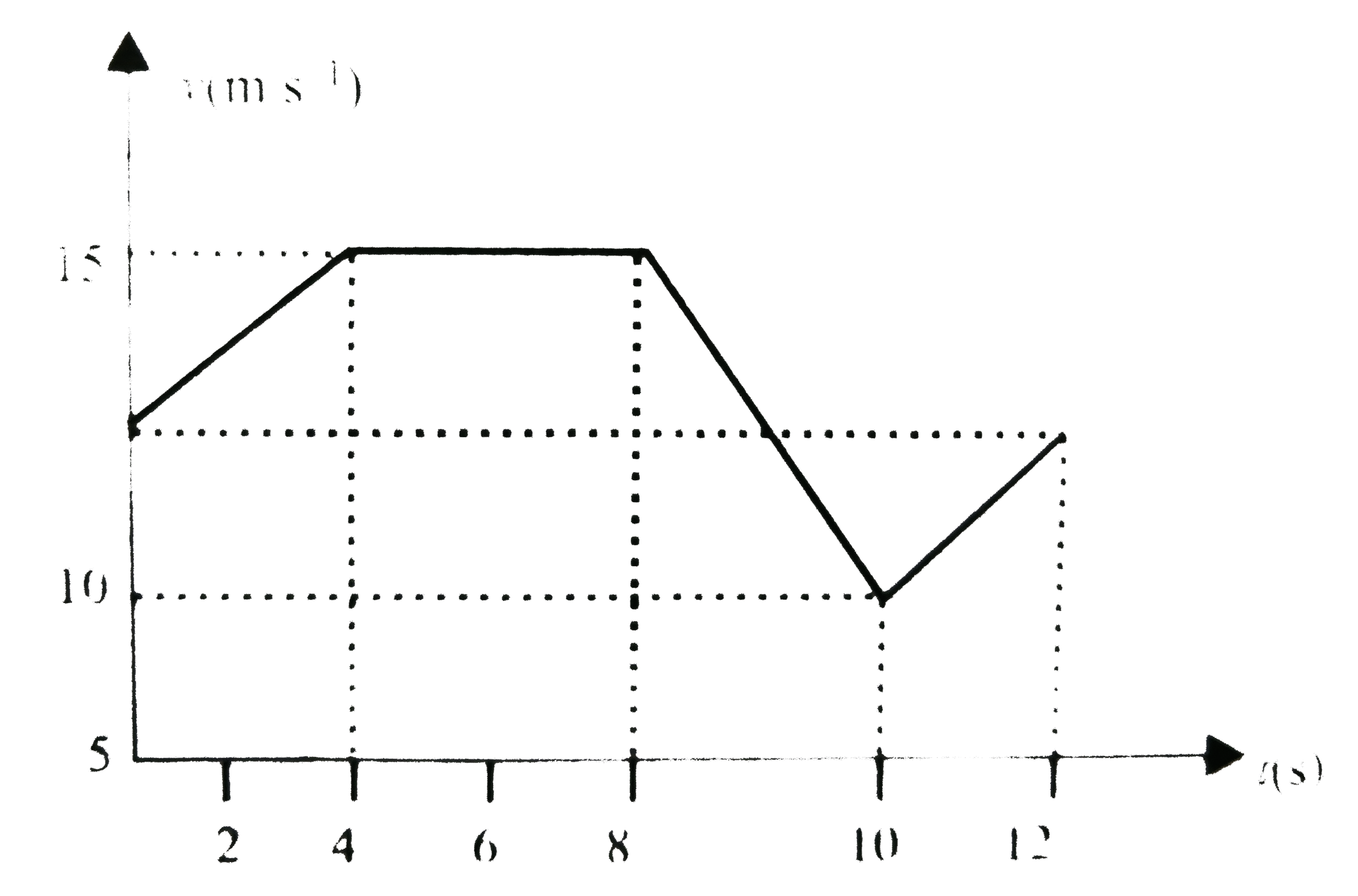 .
.
View SolutionThe displacement - time (x−t) graph of a particle executing simple harmonic motion is shown in figure. The correct variation of net force F action on the particle as a function of time is

View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
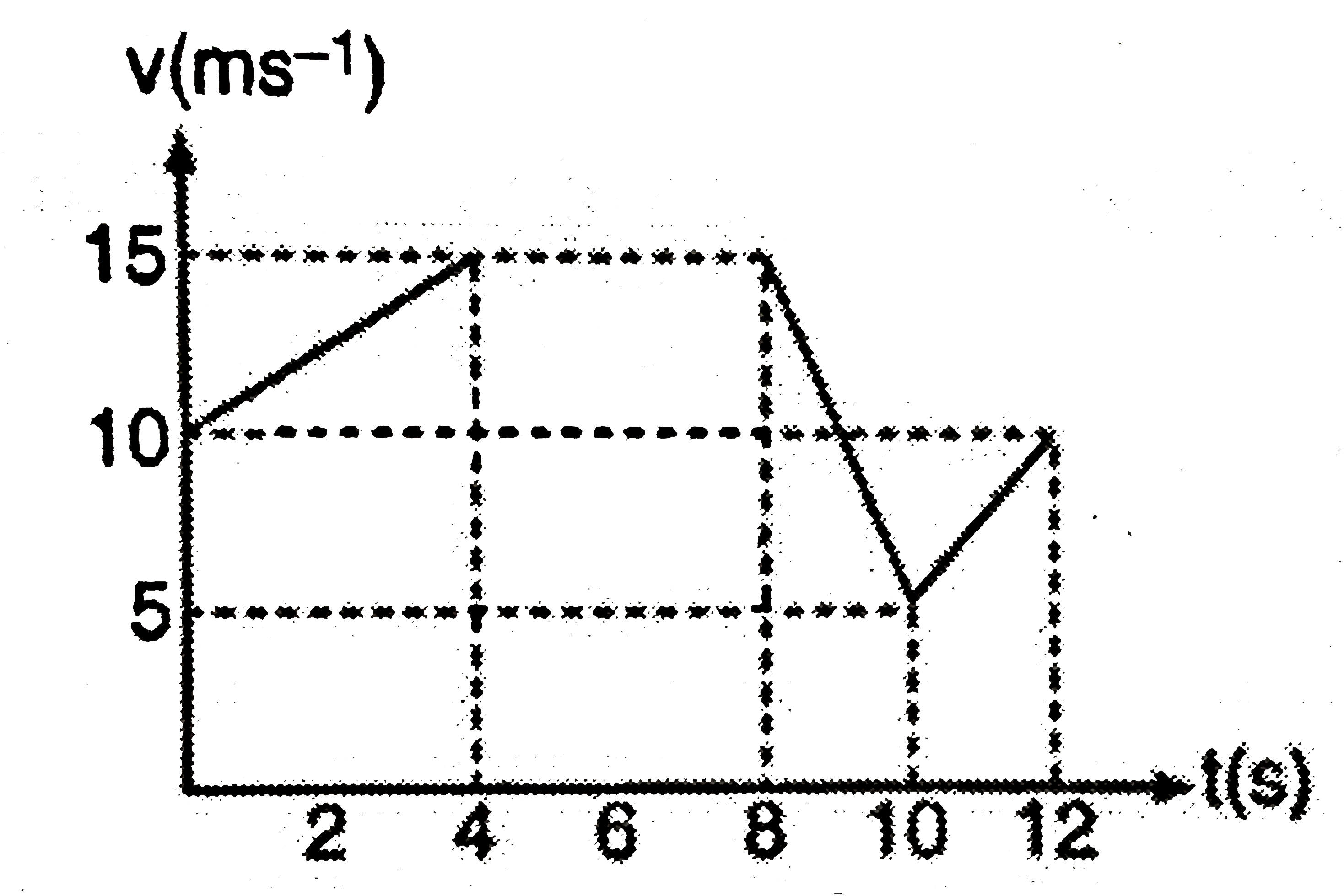
View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
View SolutionIf a particle is executing simple harmonic motion, then acceleration of particle
View Solution


