There are four charges, each with a magnitude of 2.0μC. Two are positive and two are negative. The charges are fixed to the corners of a 0.30 m square, one to a corner, in such a way that the net force on any charge is directed toward the center of the square. Find the magnitude of the net electrostatic force experienced by any charge.
0.20 N
0.57 N
0.37 N
0.16 N
The correct Answer is:C
To find the magnitude of the net electrostatic force experienced by any charge in the given configuration, we can follow these steps:
Step 1: Understanding the Configuration
We have four charges arranged at the corners of a square with a side length of 0.30 m. The charges are:
- Two positive charges (+2 µC each)
- Two negative charges (-2 µC each)
The configuration is such that the net force on any charge is directed toward the center of the square.
Step 2: Identify the Forces Acting on One Charge
Let's consider one of the positive charges located at one corner of the square. The forces acting on this charge are due to the two negative charges located at the opposite corners.
Step 3: Calculate the Distance Between Charges
The distance between the positive charge and each negative charge is the diagonal of the square. The diagonal d of a square with side length a is given by:
d=a√2=0.30√2 m
Step 4: Calculate the Electrostatic Force Between Charges
Using Coulomb's Law, the force F between two point charges is given by:
F=k|q1q2|r2
where:
- k=9×109N m2/C2 (Coulomb's constant)
- q1=q2=2×10−6C
- r=0.30m (for the charges on the same side)
- r=0.30√2m (for the diagonal)
Force between a positive charge and a negative charge on the same side:
F1=k(2×10−6)2(0.30)2=9×1094×10−120.09=0.4N
Force between a positive charge and a negative charge on the diagonal:
F2=k(2×10−6)2(0.30√2)2=9×1094×10−120.18=0.2N
Step 5: Calculate the Resultant Force
The net force on the positive charge is the vector sum of the forces F1 and F2. Since F1 is directed towards one negative charge and F2 towards the other, we can use the Pythagorean theorem to find the resultant force FR:
FR=√F21+F22=√(0.4)2+(0.2)2=√0.16+0.04=√0.2≈0.447N
Step 6: Conclusion
The magnitude of the net electrostatic force experienced by any charge is approximately 0.447N.
---
We have four charges arranged at the corners of a square with a side length of 0.30 m. The charges are:
- Two positive charges (+2 µC each)
- Two negative charges (-2 µC each)
Let's consider one of the positive charges located at one corner of the square. The forces acting on this charge are due to the two negative charges located at the opposite corners.
The distance between the positive charge and each negative charge is the diagonal of the square. The diagonal d of a square with side length a is given by:
d=a√2=0.30√2 m
Using Coulomb's Law, the force F between two point charges is given by:
F=k|q1q2|r2
where:
- k=9×109N m2/C2 (Coulomb's constant)
- q1=q2=2×10−6C
- r=0.30m (for the charges on the same side)
- r=0.30√2m (for the diagonal)
F1=k(2×10−6)2(0.30)2=9×1094×10−120.09=0.4N
F2=k(2×10−6)2(0.30√2)2=9×1094×10−120.18=0.2N
The net force on the positive charge is the vector sum of the forces F1 and F2. Since F1 is directed towards one negative charge and F2 towards the other, we can use the Pythagorean theorem to find the resultant force FR:
FR=√F21+F22=√(0.4)2+(0.2)2=√0.16+0.04=√0.2≈0.447N
The magnitude of the net electrostatic force experienced by any charge is approximately 0.447N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Linked Comprehension)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems63videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELASTICITY
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
Similar Questions
Four point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
 View Solution
View SolutionFour identical charges +Q are kept at the corners of a square ABCD. The edge length of square is a . Find net force on the charge kept at C due to the other three charges.
View Solution
Knowledge Check
- Question 1 - Select One
Four charges are arranged at the corners of a square ABCD, as shown in the adjoining figure, The force on a positive charge kept at the centre O is
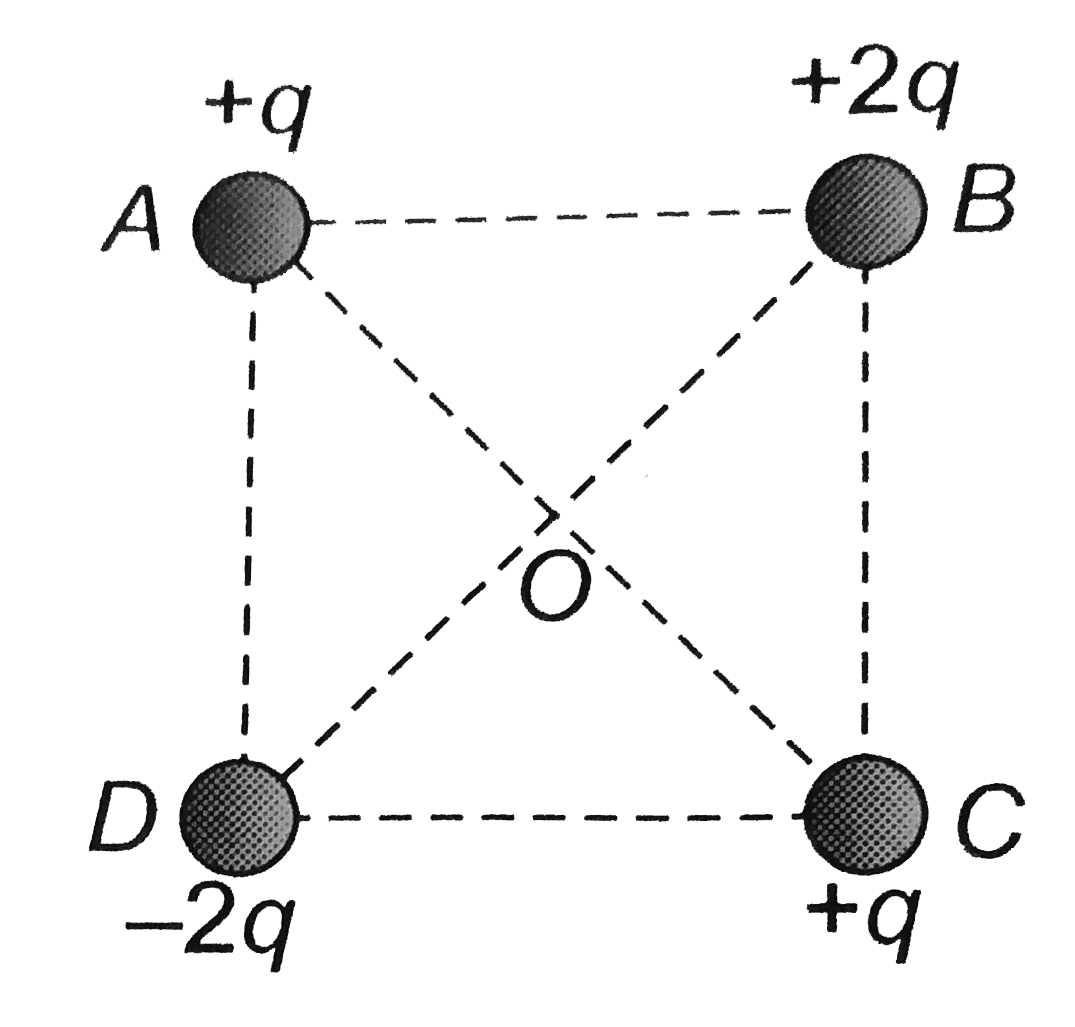 AZeroBAlong the diagonal ACCAlong the diagonal BDDPerpendicular to side AD
AZeroBAlong the diagonal ACCAlong the diagonal BDDPerpendicular to side AD - Question 2 - Select One
Four charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the ccentre O is
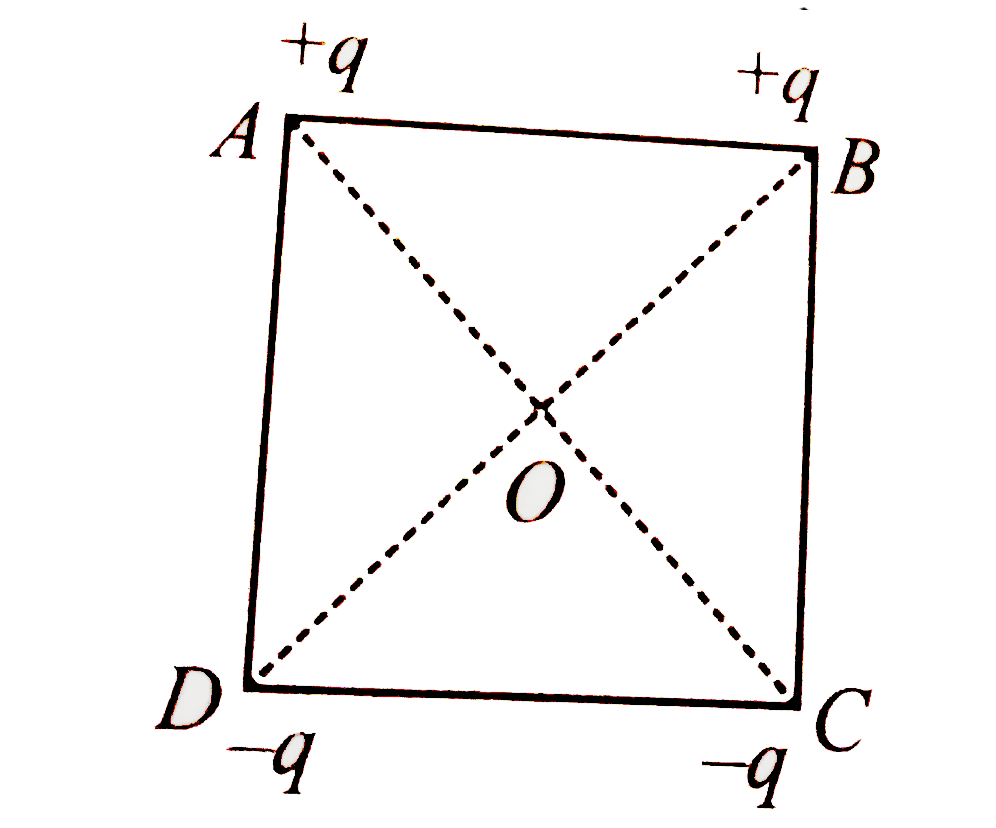 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB - Question 3 - Select One
Four charges are arranged at the corners of a square ABCD, as shown. The force on a =ve charge kept at the centre of the square is -
 AZeroBalong diagonal ACCalong diagonal BDDperpendicular to the side AB
AZeroBalong diagonal ACCalong diagonal BDDperpendicular to the side AB
Two equal positive charges are placed at two corners or a square, 'the' other two corners having neglative charges or equal magnitude. Find the field intensity in the centre of the square in the two cases.
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge QView SolutionFour point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
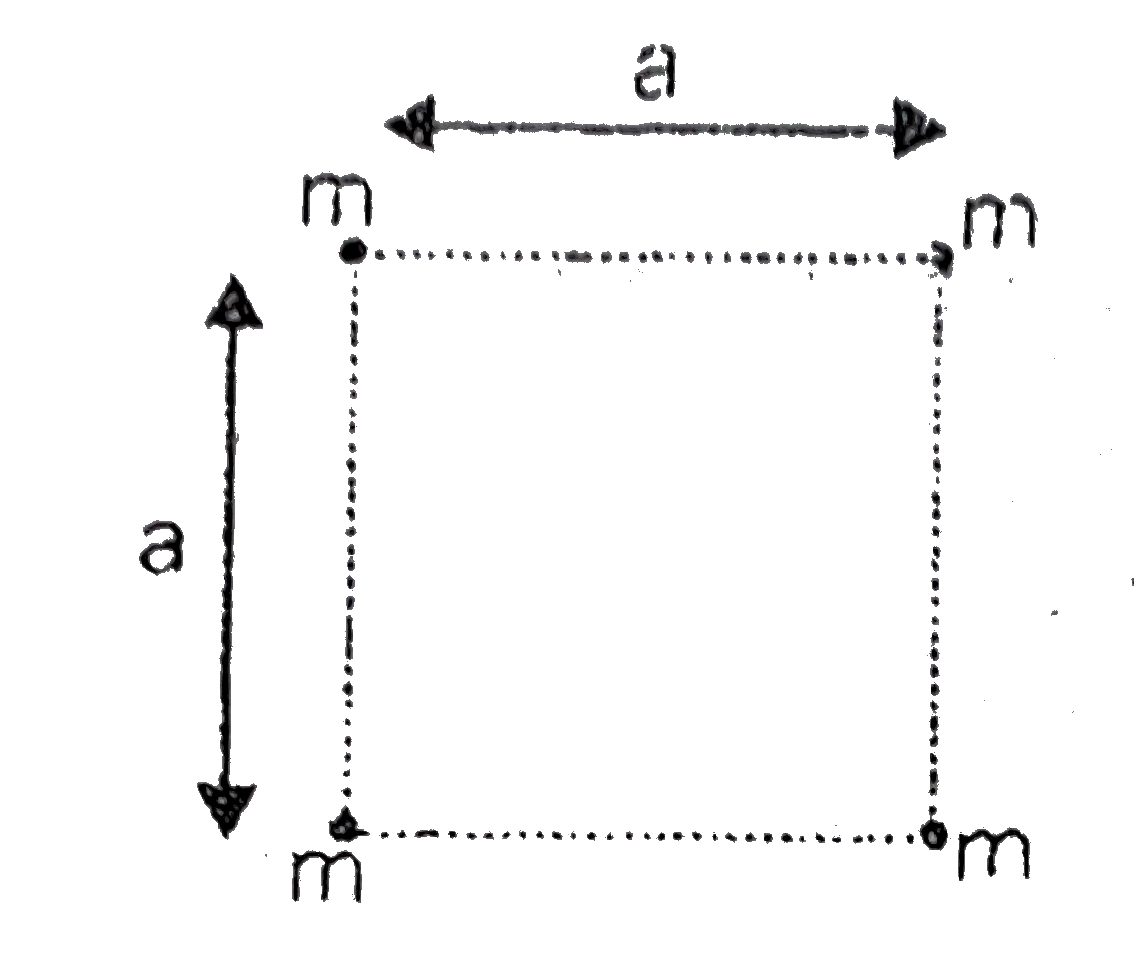 .View Solution
.View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 View Solution
View SolutionFour charges are arranged at the corners of a square ABCD, as shown. The force on a positive charge kept at the centre of the square is
 View Solution
View Solution

