There have been suggestions that the value of the gravitational constant G becomes smaller when considered over very large time period (in billions of years) in the future. If that happens, for our earth
nothing will change.
we will become hotter after billions of years.
we will be going around but not strictly in closed orbits.
after sufficiently long time we will leave the solar system.
The correct Answer is:C, D
To analyze the implications of a decreasing gravitational constant G over billions of years on Earth, we can break down the problem step by step.
1. Understanding the Gravitational Force:
The gravitational force F between two masses (Earth and Sun) is given by Newton's law of gravitation:
F=G⋅M1⋅M2R2
where M1 is the mass of the Earth, M2 is the mass of the Sun, R is the distance between the centers of the two masses, and G is the gravitational constant.
2. Assumption of Decreasing G:
If G decreases over a long time period (billions of years), it implies that the gravitational force F will also decrease since F is directly proportional to G.
3. Effect on Gravitational Force:
As G decreases, the gravitational force F acting between the Earth and the Sun will decrease:
F∝G⇒F decreases as G decreases.
4. Implications of Decreasing Force:
A decrease in gravitational force means that the attraction between the Earth and the Sun weakens. Since the gravitational force is what keeps the Earth in orbit around the Sun, a reduction in this force will affect the orbital dynamics.
5. Change in Orbital Radius:
If the gravitational force F decreases, the Earth will not be held as tightly in its orbit. This leads to an increase in the orbital radius R because:
F=G⋅M1⋅M2R2⇒If F decreases, R must increase.
6. Long-Term Consequence:
As R increases, the Earth will eventually move away from its current orbit. If this trend continues over billions of years, it could lead to the Earth leaving the solar system entirely.
7. Conclusion:
Therefore, if the gravitational constant G continues to decrease over a long time, the Earth could potentially drift away from the Sun and leave the solar system.
Final Answer:
If the gravitational constant G decreases over billions of years, the Earth could leave the solar system due to the weakening gravitational attraction between the Earth and the Sun.
The gravitational force F between two masses (Earth and Sun) is given by Newton's law of gravitation:
F=G⋅M1⋅M2R2
where M1 is the mass of the Earth, M2 is the mass of the Sun, R is the distance between the centers of the two masses, and G is the gravitational constant.
If G decreases over a long time period (billions of years), it implies that the gravitational force F will also decrease since F is directly proportional to G.
As G decreases, the gravitational force F acting between the Earth and the Sun will decrease:
F∝G⇒F decreases as G decreases.
A decrease in gravitational force means that the attraction between the Earth and the Sun weakens. Since the gravitational force is what keeps the Earth in orbit around the Sun, a reduction in this force will affect the orbital dynamics.
If the gravitational force F decreases, the Earth will not be held as tightly in its orbit. This leads to an increase in the orbital radius R because:
F=G⋅M1⋅M2R2⇒If F decreases, R must increase.
As R increases, the Earth will eventually move away from its current orbit. If this trend continues over billions of years, it could lead to the Earth leaving the solar system entirely.
Therefore, if the gravitational constant G continues to decrease over a long time, the Earth could potentially drift away from the Sun and leave the solar system.
If the gravitational constant G decreases over billions of years, the Earth could leave the solar system due to the weakening gravitational attraction between the Earth and the Sun.
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - FILL IN THE BLANKS
11 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE A
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - CURIOSITY QUESTION
1 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
A great physicist of this century (P. A. M. Dirac) loved playing with numerical values of fundamental constant of nature. This led him to an instreasing observaion. Dirac found that form the basic constant of atomin physice (c,e, mass of electron mass of proton) and the gravitational constant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (≈15billionyears). Form the table of fundamental constants in this book, try to see if you too can construct this number (or any other instresting number you can think of). if its coincidence with the age of the universe ware significant, what would this imply for the constancy of fundamental constants ?
View SolutionFill in the following blanks with suitable words:
(a) The acceleration due to gravity on the moon is about .
(b) In order that the force of gravitation between two bodies may become noticeable and cause motion, one of the bodies must have an of that on the earth. extremely large
( c) The weight of an object on the earth is about ........of its weight on the moon.
(d) The weight of an object on the moon is about
(e) The value of g on the earth is about .... of that on the moon.
View Solution
Knowledge Check
There have been suggestions that the value of the gravitational constant G becomes smaller when considered over very large time period (in billions of years) in the future. If the happens for our earth.
Anothing will changeBwe will becomes hotter after billions of years.Cwe will be going around but not strictly in losed orbitsDafter sufficiently long time we will leave the solar systemA wire of mass m and length l is placed on a smooth incline making an angle θ with the horizontal, whose front view is shown in Fig. When a finite amount of charge is passed through it in an infinitesimal time, the wire immediately acquires some velocity and then ascends the incline by a distance s. For this small duration, we can neglect the gravitational force because the current can be considered very large due to small time duration. The amount of charge passed through the wire is
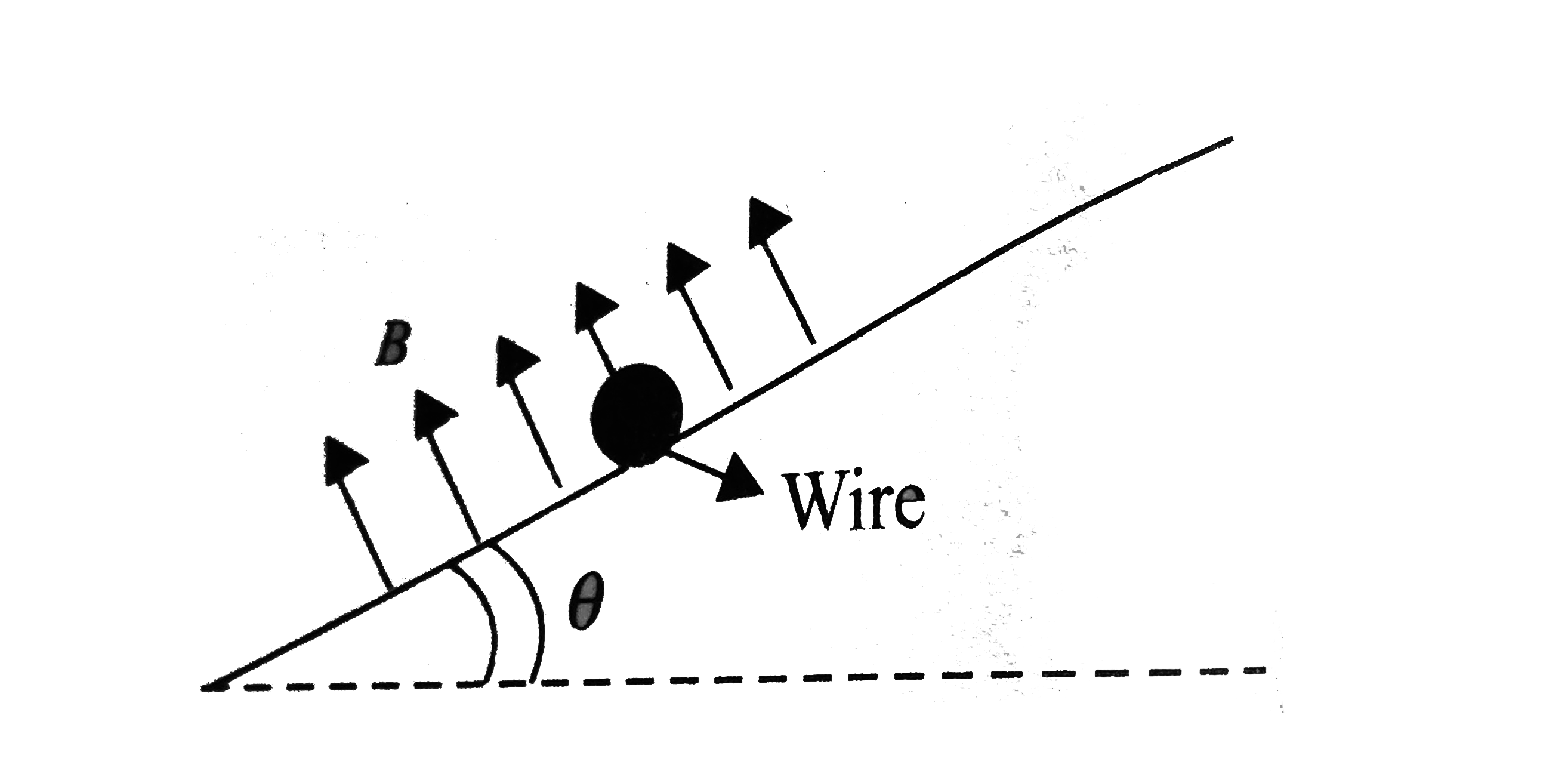 Am√2gssinθBlBmvBlCm√2gssinθBlcosθDinformation insufficient
Am√2gssinθBlBmvBlCm√2gssinθBlcosθDinformation insufficientTime period (T) of pendulum is directly proportional to the square root of length of string by which bob is attached to a fixed point and inversely proportional to the square root of gravitational constant 'g'. Time period of a bob is 3 seconds when the gravitational constant g is 4 msec2 and length of string is 9 metre, what is the time period of a bob having a string length of 64 metre and gravitational constant g is 16 msec2?
A4 secondsB12 secondsC16 secondsD10 seconds
Fundamental forces in nature have been classified as : Gravitational forces, weak forces, electromagnetic forces and nuclaer forces. Gravitational forces are weakest of all forces and nuclear forces are the stronges of all. Whereas gravitational forces operate over very long distance, the nuclear forces are confined only within the nucleus. Read the above passage and answer the following questions : (i) Which forces are central forces ? (ii) Which forces are non conservative forces ? (iii) What value of life do you learn from this study ?
View SolutionAn object falling through a fluind is observed to have acceleration given by a=g−bv where g= gravitational acceleration and (b) is constant. After a long time of rlease. It is observed to fall with constant speed. What must be the value of constant speed ?
View SolutionTime period (T) of pedulum is directly proprortional to the square root of length of string by which bob is attached to a fixed point and iknversely proportional to the square root of gravitational constant g. Time period of a bob is 3 seconds when the gravitational constannt g is 4m/sec2 and length of string is 9 metre, what is the time period of a bob having astring of length 64 metre and gravitational constant 16m/sec2?
View SolutionCertain amount of a gas exerts some pressure on its walls at a particular temperature. It hasa been found.that by reducing the volume of the gas to 14 of its original value the pressure becomes 4 times that of the initial value of constant temperature. this happens because:
View SolutionToday there are enough hydrogen bombs of the greatest destructive power to wipe out all life on our planet. Will we make even larger bombs in future? We can, if we want to, but even for the most overwhelming military purposes we do not need to. We have already reached some sort of limit. How much more dangerous can the situation get? At the present time, we are very near the edge of death. Every year or two in some major international crises - there is serious probability of an 'accident' that would lead to nuclear war. Dedicated men have worked hard and long in these situations to avoid a nuclear incident, but we may not continue to be so lucky. Next time it may be a nuclear threat or a mad man or a mistaken junior officer or just faulty equipment. It is foolish of us to boast of the decrease in our death rate and increase in the length of individual human lives in the 20th century, as long as this nuclear danger is so uncontrolled. This situation cannot continue. We cannot live very long walking on loose at the edge of a cliff. Either in ten, twenty or thirty years we fall over the nuclear cliff, or else very soon, before that time runs out, we have to arrive at an international understanding and move back from the danger.
In the phrase' before that time runs out (last para) 'that time' refers to the time
View Solution
