There is a, and four charges +q, +q, -q and -q are fixed at the four corners of square. See the figure for the placement of charges.
Calculate:
(i) Electric potential at point O.
(ii) Work done to move a charge +e from point O to point B.
(iii) Work done to move a charge +e from point O to A.

The given arrangement is shown below:

Let the distance of each point charge from O be r.
Then r=OP=OQ=OR=OS
Also, PR2=PS2+SR2
Here, PS=SR=RQ=PQ=a
∴PR2=a2+a2⇒PR=√2a
∴r=PO=√2a2=a√2
(i) Potential at the centre O is :
VO=14πε0[qr+qr−qr−qr]=0
(ii) To find the work done to move a charge from O to B, we need to first find the electric potential at point B.
Potential at point B will be given by:
VB=14πε0[qPB+qQB−qRB−qSB]
Also, PB2+PD2+DB2
=(a2)2+a2=5a24
⇒PB=√5a2
Also, SB=PB=√5a2andQB=RB=a2
∴VB=9×109⎡⎢⎣q√5a2+qa2−qa2−q√5a2⎤⎥⎦=0
Since, VB=VO=0
∴ No work will be done on moving a charge from O to B.
(iii) To find the work the work done to move a charge from O to A, we need to first find the electric potential at point A.
Potential at point A will be given by:
VA=14πε0[qPA+qQA−qRA−qSA]
Also, RA2=AC2+CR2=a2+(a2)2=5a22
⇒RA=√5a2
Also, SA=RA=√5a2andPA=QA=a2
∴VA=9×109⎡⎢⎣aa2+qa2−q√5a2−q√5a2⎤⎥⎦
=9×109⎡⎢⎣2qa2−2q√5a2⎤⎥⎦
=9×109[4qa−4q√5a]
=9×109×4qa[1−1√5]
=36qa×109(1−1√5)
∴ Work done in moving a charge +e from O to A will be: (this work is done by an external agent so its potential difference is taken as final minus initial)
VA−VO=WOAe
⇒VA−0=WOAe
⇒WOA=eVA=e×36qa×109(1−1√5)
=36qea×109(1−1√5)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 110videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 221videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Four electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is
 View Solution
View SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the resultant electric force on a charge Q,View Solution
Knowledge Check
- Question 1 - Select One
Four electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is
 A14πε02LL(1+1√5)B14πε02LL(1−1√5)CzeroD14πε02LL(1+√5)
A14πε02LL(1+1√5)B14πε02LL(1−1√5)CzeroD14πε02LL(1+√5) - Question 2 - Select One
Four electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is
 A14πε02qL(1+√5)B14πε02qL(1+1√5)CzeroD14πε02qL(1−1√5)
A14πε02qL(1+√5)B14πε02qL(1+1√5)CzeroD14πε02qL(1−1√5) - Question 3 - Select One
Four charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
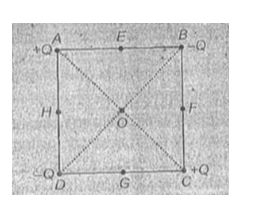 AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
Four charges + q, –q, + q and –q are put together on four corners of a square as shown in figure. The work done by external agent in slowly assembling this configuration is
 View Solution
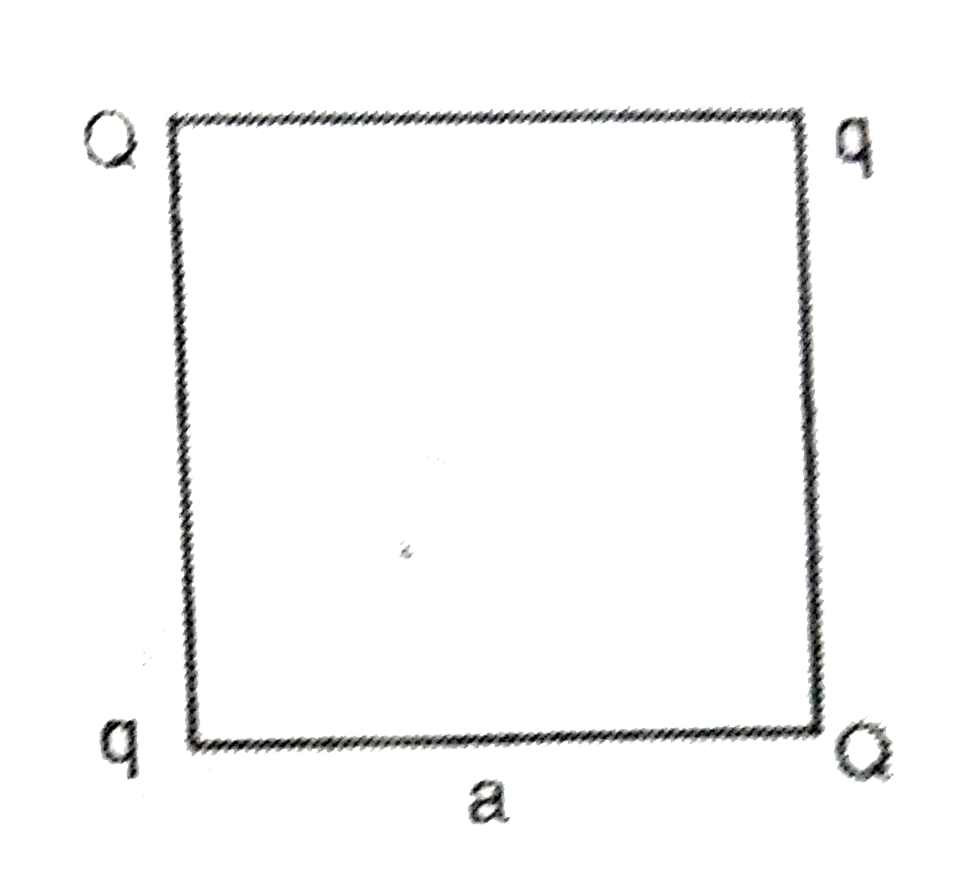
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge QView SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the Potential energy of this system.View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
 View Solution
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
 View Solution
View Solution

