There is a constant homogeneous electric field of 100Vm−1 within the region x=0andx=0.167m pointing in x-direction. There is a constant homogeneous mangetic field B within the region x=0.167mandx=0.334m pointing in the z-direction. A proton at rest at the origin is released in positive x-direction. Find the minimum strength of the magnetic field B, so that the proton is detected back at x=0,y=0.167m. (mass of proton =1.67×10−27kg)
To solve the problem, we need to analyze the motion of a proton in the given electric and magnetic fields. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- There is a constant electric field E=100V/m in the region x=0 to x=0.167m.
- There is a constant magnetic field B in the region x=0.167m to x=0.334m pointing in the z-direction.
- The proton is released from rest at the origin and moves in the positive x-direction.
- The mass of the proton m=1.67×10−27kg.
- We need to find the minimum strength of the magnetic field B such that the proton is detected back at (x=0,y=0.167).
Step 2: Calculate the Acceleration of the Proton
The force acting on the proton due to the electric field is given by:
F=qE
where q=1.6×10−19C (charge of the proton).
The acceleration a of the proton can be calculated using Newton's second law:
a=Fm=qEm
Substituting the values:
a=(1.6×10−19C)(100V/m)1.67×10−27kg=0.96×1010m/s2
Step 3: Calculate the Velocity of the Proton at x=0.167m
Using the kinematic equation:
v2=u2+2as
where u=0 (initial velocity), a=0.96×1010m/s2, and s=0.167m:
v2=0+2(0.96×1010)(0.167)
Calculating v:
v=√2×0.96×1010×0.167≈0.58×105m/s
Step 4: Determine the Radius of the Circular Path in the Magnetic Field
When the proton enters the magnetic field, it experiences a magnetic force given by:
F=qvB
This force acts as the centripetal force:
F=mv2r
Setting these equal gives:
qvB=mv2r
Rearranging for B:
B=mvqr
Step 5: Calculate the Radius of the Circular Path
The radius r of the circular path is given by:
r=0.1672=0.0835m
Step 6: Substitute Values to Find B
Substituting the known values into the equation for B:
B=(1.67×10−27kg)(0.58×105m/s)(1.6×10−19C)(0.0835m)
Calculating B:
B≈7.19×10−3T
Final Answer
The minimum strength of the magnetic field B required is approximately:
B≈7.19mT
- There is a constant electric field E=100V/m in the region x=0 to x=0.167m.
- There is a constant magnetic field B in the region x=0.167m to x=0.334m pointing in the z-direction.
- The proton is released from rest at the origin and moves in the positive x-direction.
- The mass of the proton m=1.67×10−27kg.
- We need to find the minimum strength of the magnetic field B such that the proton is detected back at (x=0,y=0.167).
The force acting on the proton due to the electric field is given by:
F=qE
where q=1.6×10−19C (charge of the proton).
a=Fm=qEm
Substituting the values:
a=(1.6×10−19C)(100V/m)1.67×10−27kg=0.96×1010m/s2
Using the kinematic equation:
v2=u2+2as
where u=0 (initial velocity), a=0.96×1010m/s2, and s=0.167m:
v2=0+2(0.96×1010)(0.167)
Calculating v:
v=√2×0.96×1010×0.167≈0.58×105m/s
When the proton enters the magnetic field, it experiences a magnetic force given by:
F=qvB
This force acts as the centripetal force:
F=mv2r
Setting these equal gives:
qvB=mv2r
Rearranging for B:
B=mvqr
The radius r of the circular path is given by:
r=0.1672=0.0835m
Substituting the known values into the equation for B:
B=(1.67×10−27kg)(0.58×105m/s)(1.6×10−19C)(0.0835m)
Calculating B:
B≈7.19×10−3T
The minimum strength of the magnetic field B required is approximately:
B≈7.19mT
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.213videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A particle of mass 20g experiences a gravitational force of 4.0N along positive x - direction. Find the gravitational field at that point.
View SolutionA proton is moving along Z-axis in a magnetic field. The magnetic field is along X-axis. The proton will experience a force along
View SolutionA current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionA plane electromagnetic wave propagating in the x-direction has wavelength of 6.0mm. The electric field is in the y-direction and its maximum magnitude of 33Vm−1. The equation for the electric field as function of x and l is
View SolutionA uniform electric field is present in the positive x - direction. If the intensity of the field is 5NC−1 then find the potential difference (VB−VA) between two points A (0 m, 2 m) and B (5 m, 3 m).
View SolutionAn electron is moving along +x direction with a velocity of 6×106ms−1 . It enters a region of uniform electric field of 300 V/cm pointing along + y direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the x direction will be :
View SolutionThe electric field in a region is radially outward with magnitude E = 2r. The charge contained in a sphere of radius a = 2m centerd at the origin is 4xπε0. Find the value of x.
View SolutionIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed V=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp (mass of proton) =1.6×10−27kg and e (magnitude of electronic charge) =1.6×10−19C.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
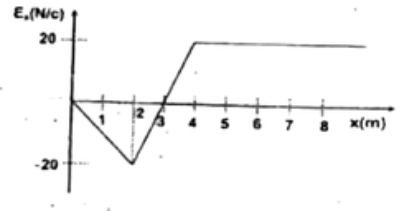
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m isView SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View Solution

