There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
T=2π√2l3g
T=π√l3g
T=2π√l3g
T=2π√lg
The correct Answer is:A
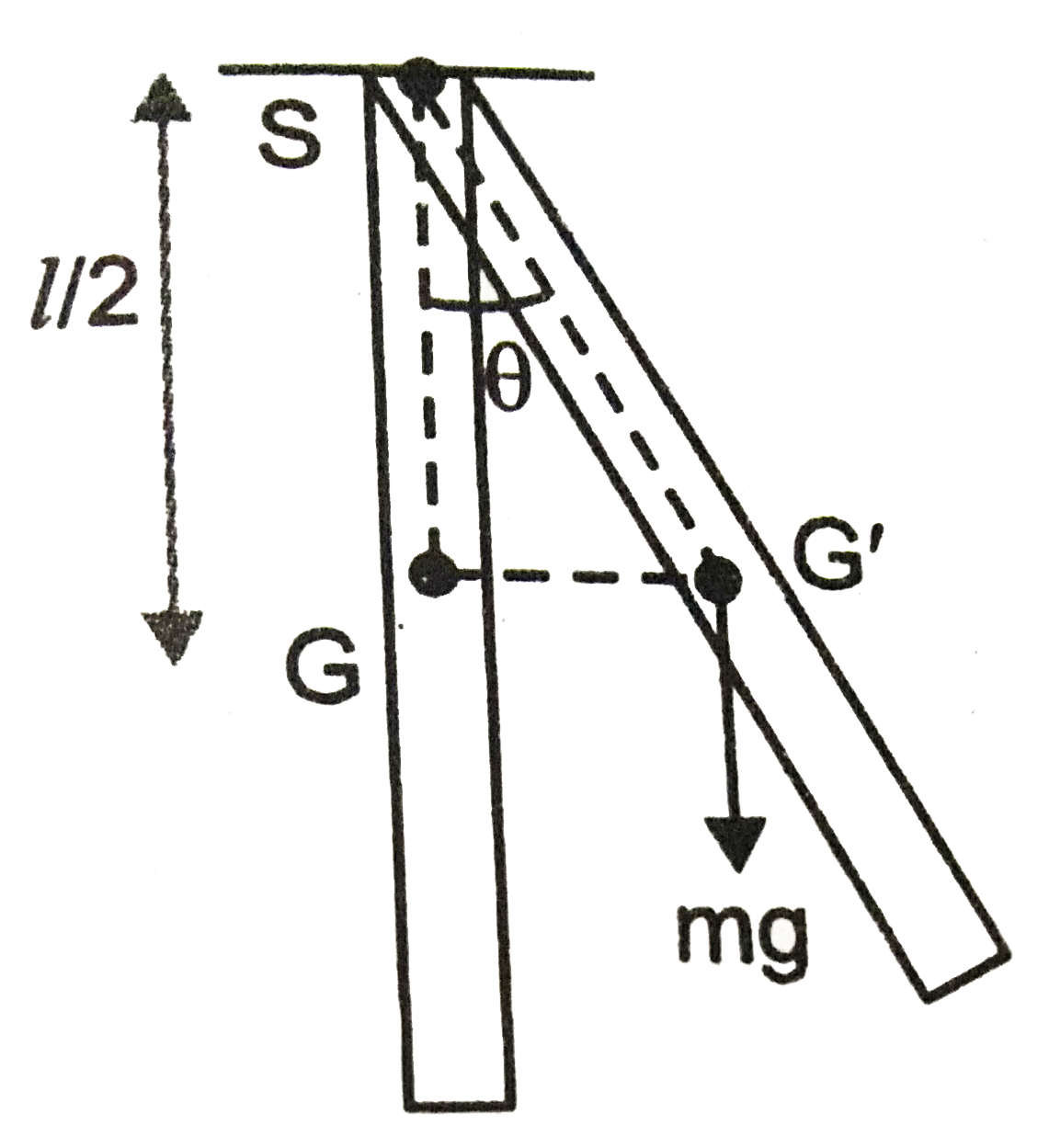
When the rod is at position shown in figure , the restoring torque ono the rod is
τ=−mg×(GG′)=(−mg)l2θ …(i)
τ∝θ
(∵mgl2= a constant for a given position )
Therefore, if the rod is left free, if will execute angular SHM.
Comparing (i) with τ=−kθ
We have, spring factor, k=mgl2
Inertia factor = moment of indertia of rod about point of suspension as axis
=ml212+m(l2)2=ml23
As, time period T=2π√Inertiafactorspringfactor
=2π√ml2/3mgl/2=2π√2l3g
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question8videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Assertion-Reason Type Questions23videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II14videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
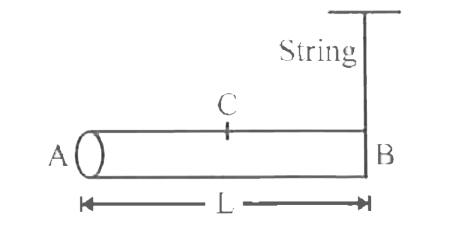
A uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
 View Solution
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK - Question 2 - Select One
Two particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
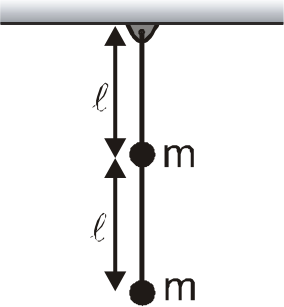 A3l2B103C5l3DNone of these
A3l2B103C5l3DNone of these - Question 3 - Select One
Two particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
 A3l2B10l3C5l3DNone of these
A3l2B10l3C5l3DNone of these
A spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
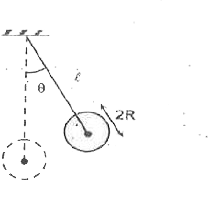 View Solution
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 View Solution
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 View Solution
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 View Solution
View Solution

