There is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as Dwhere particle finally strikes. Acceleration due to gravity g=10m/s2
Maximum height above the ground attained by particle is
20m
30m
40m
60m
The correct Answer is:c
To solve the problem step by step, we will analyze the motion of the particle projected from the top of the tower and calculate the maximum height it reaches above the ground.
Step 1: Understand the Given Information
- Height of the tower (h_tower) = 20 m
- Initial speed of the particle (u) = 20 m/s (upward)
- Acceleration due to gravity (g) = 10 m/s² (downward)
Step 2: Identify Points
- Point A: Top of the tower (where the particle is projected)
- Point B: Maximum height reached by the particle
- Point C: Point A during the downward journey (when the particle returns to the top of the tower)
- Point D: Ground level (bottom of the tower)
Step 3: Calculate the Maximum Height (h_max) Above Point A
We will use the third equation of motion to find the maximum height reached by the particle above point A (h_max):
v2=u2+2as
Where:
- v = final velocity at maximum height = 0 m/s (at point B)
- u = initial velocity = 20 m/s
- a = acceleration = -g = -10 m/s² (negative because it is acting downward)
- s = displacement from A to B = h_max
Substituting the values into the equation:
0=(20)2+2(−10)(hmax)
0=400−20hmax
20hmax=400
hmax=40020=20 m
Step 4: Calculate the Total Maximum Height Above Ground
The total maximum height (H_total) above the ground is the sum of the height of the tower and the maximum height reached above point A:
Htotal=htower+hmax
Htotal=20 m+20 m=40 m
Final Answer
The maximum height attained by the particle above the ground is 40 meters.
---
- Height of the tower (h_tower) = 20 m
- Initial speed of the particle (u) = 20 m/s (upward)
- Acceleration due to gravity (g) = 10 m/s² (downward)
- Point A: Top of the tower (where the particle is projected)
- Point B: Maximum height reached by the particle
- Point C: Point A during the downward journey (when the particle returns to the top of the tower)
- Point D: Ground level (bottom of the tower)
We will use the third equation of motion to find the maximum height reached by the particle above point A (h_max):
v2=u2+2as
Where:
- v = final velocity at maximum height = 0 m/s (at point B)
- u = initial velocity = 20 m/s
- a = acceleration = -g = -10 m/s² (negative because it is acting downward)
- s = displacement from A to B = h_max
0=(20)2+2(−10)(hmax)
0=400−20hmax
20hmax=400
hmax=40020=20 m
The total maximum height (H_total) above the ground is the sum of the height of the tower and the maximum height reached above point A:
Htotal=htower+hmax
Htotal=20 m+20 m=40 m
The maximum height attained by the particle above the ground is 40 meters.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (ASSERTION REASON)
9 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATCHING TYPE QUESTIONS)
2 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))
13 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
There is one tower of height h. one particle A is projected upward from top of the tower with a speed u1 at time t=0 . At time t=t0 another particle B is projected upward from the bottom of the tower with a speed u2. When will the particles cross each other?
View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View Solution
Knowledge Check
There is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
Time taken by the particle to reach the ground isA2sB4sC2√2sD(2+2√2)sThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
How much time the particle takes to cross the point C after being projected from point A.A1sB2sC3sD4sAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A20√3mB20√3mC√320mDNone of these
Height of a tower is 125m and a particle is dropped from rest from the top of the tower. After two seconds of its fall, another particle is projected downwards with a speed u such that both the particles reach the ground simultaneously. What is the value of u?
View SolutionA particle is dropped from the top of a tower. If it falls half of the height of the tower in its last second of journey, find the time of journey.
View SolutionA particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
View SolutionA particle is dropped from the top of a tower. During its motion it covers 925 part of height of tower in the last 1 second Then find the height of tower.
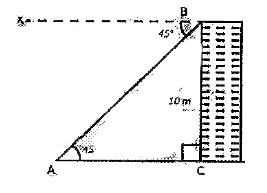
View SolutionSuppose angle of depression from top of the tower to point A is 45∘ and height of tower is 10 m. What is the distance of point A from the building?
View Solution
