Three blocks A, B and C of masses 5 kg, 10 kg and 15 kg respectively connected by two ideal strings are present on a smooth horizontal surface. An external horizontal force of 30 N acts on the block A to pull the system. Find the difference in the tensions in strings connecting A and B and, B and C.
The correct Answer is:10
To solve the problem step-by-step, we will follow these steps:
Step 1: Identify the masses and the external force
We have three blocks:
- Block A: mass mA=5kg
- Block B: mass mB=10kg
- Block C: mass mC=15kg
An external force F=30N is applied to block A.
Step 2: Calculate the total mass of the system
The total mass M of the system is the sum of the masses of the three blocks:
M=mA+mB+mC=5kg+10kg+15kg=30kg
Step 3: Calculate the acceleration of the system
Using Newton's second law, the acceleration a of the system can be calculated as:
F=M⋅a⟹a=FM=30N30kg=1m/s2
Step 4: Analyze the forces on block C
Since block C is only connected to block B by a string, the tension T2 in the string connecting B and C can be calculated using the equation:
T2=mC⋅a=15kg⋅1m/s2=15N
Step 5: Analyze the forces on block B
Now, we will analyze block B, which is connected to block A by another string. The tension T1 in the string connecting A and B can be calculated by considering the forces acting on block B:
T1−T2=mB⋅a
Substituting the known values:
T1−15N=10kg⋅1m/s2
T1−15N=10N
T1=10N+15N=25N
Step 6: Find the difference in tensions
Now, we can find the difference in the tensions T1 and T2:
Difference=T1−T2=25N−15N=10N
Final Answer
The difference in the tensions in the strings connecting A and B and B and C is 10N.
---
We have three blocks:
- Block A: mass mA=5kg
- Block B: mass mB=10kg
- Block C: mass mC=15kg
The total mass M of the system is the sum of the masses of the three blocks:
M=mA+mB+mC=5kg+10kg+15kg=30kg
Using Newton's second law, the acceleration a of the system can be calculated as:
F=M⋅a⟹a=FM=30N30kg=1m/s2
Since block C is only connected to block B by a string, the tension T2 in the string connecting B and C can be calculated using the equation:
T2=mC⋅a=15kg⋅1m/s2=15N
Now, we will analyze block B, which is connected to block A by another string. The tension T1 in the string connecting A and B can be calculated by considering the forces acting on block B:
T1−T2=mB⋅a
Substituting the known values:
T1−15N=10kg⋅1m/s2
T1−15N=10N
T1=10N+15N=25N
Now, we can find the difference in the tensions T1 and T2:
Difference=T1−T2=25N−15N=10N
The difference in the tensions in the strings connecting A and B and B and C is 10N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Matrix-Match)7videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
Three blocks, P, Q and R of masses 5 kg, 4 kg and 3 kg respectively are connected by a light inextensible string and they are moved on a smooth horizontal plane. If a force of 24 N is applied to the string connected to R, tensions T1andT2 in the string are
 View Solution
View SolutionThree blocks of masses 5 kg, 10 kg and 15 kg are connected to - light inextensible string placed on smooth horizontal table as shown below.
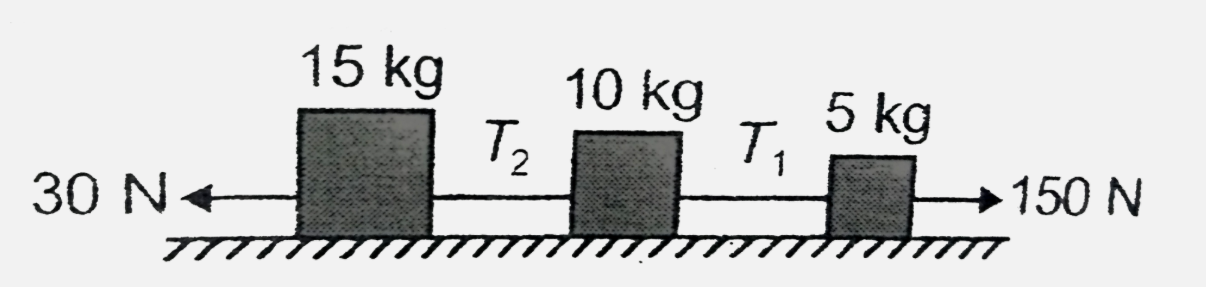
T1T2 will beView Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N - Question 2 - Select One
Two Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
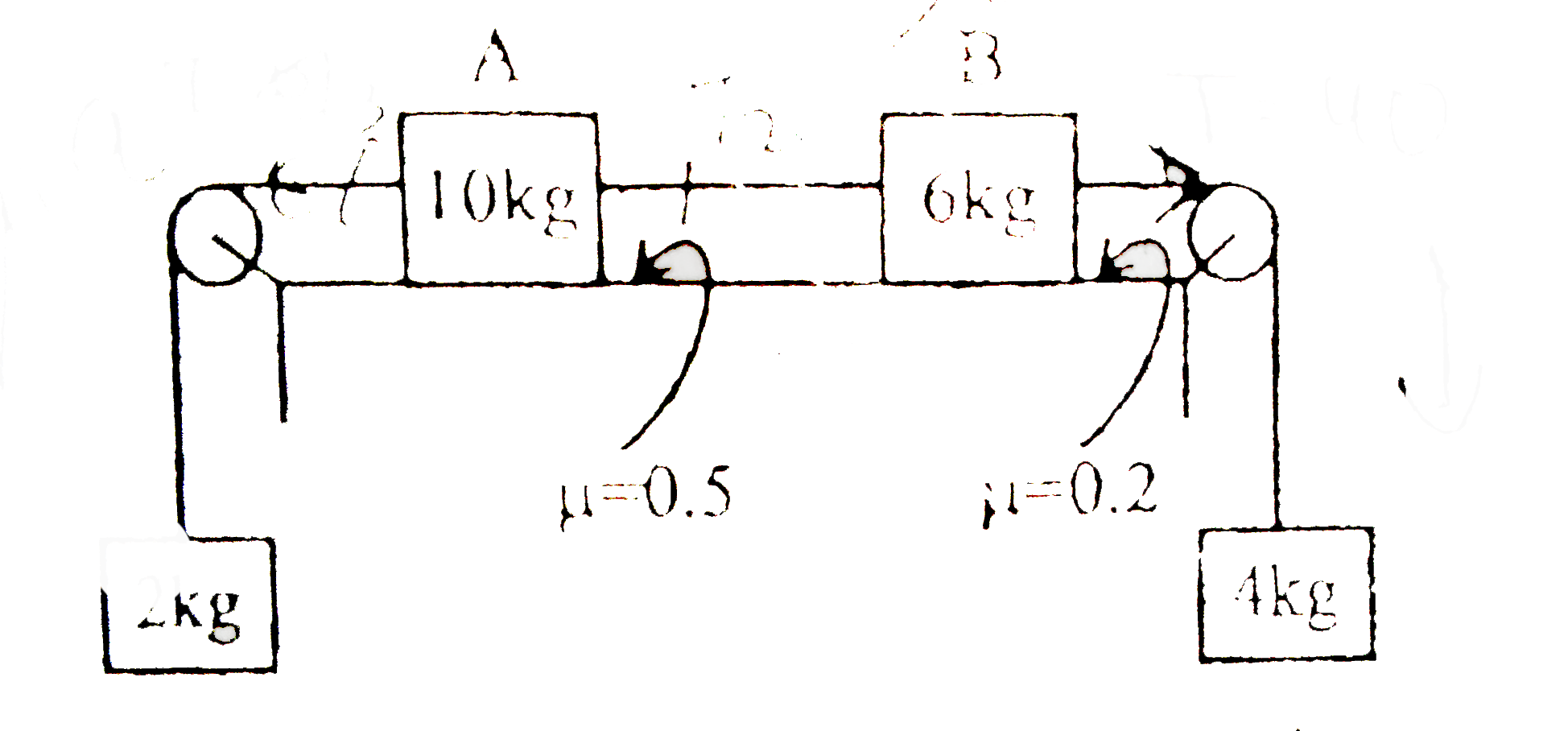 A0B76C1011D3011
A0B76C1011D3011 - Question 3 - Select One or More
Four blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
Three blocks of masses m1=10kg,m2=20kg,m3=30kg are connected by strings on smooth horizontal surface and pulled by a force of 60 N. Find the acceleration of the system and tensions in the string.
 View Solution
View SolutionThree blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.
 View Solution
View SolutionTwo bodies of masses 10 kg and 20 kg respectively kept on a smooth horizontal surface are tied to the ends of a light string A horizontal force F = 600 N is applied to (i) A and (ii) B aling the direction of string . What is the tension in the string in each case ?
View SolutionThree blocks connected together by strings are pulled along a horizontal surface by applying a force F.IfF=36N What is the tension T2 ?.
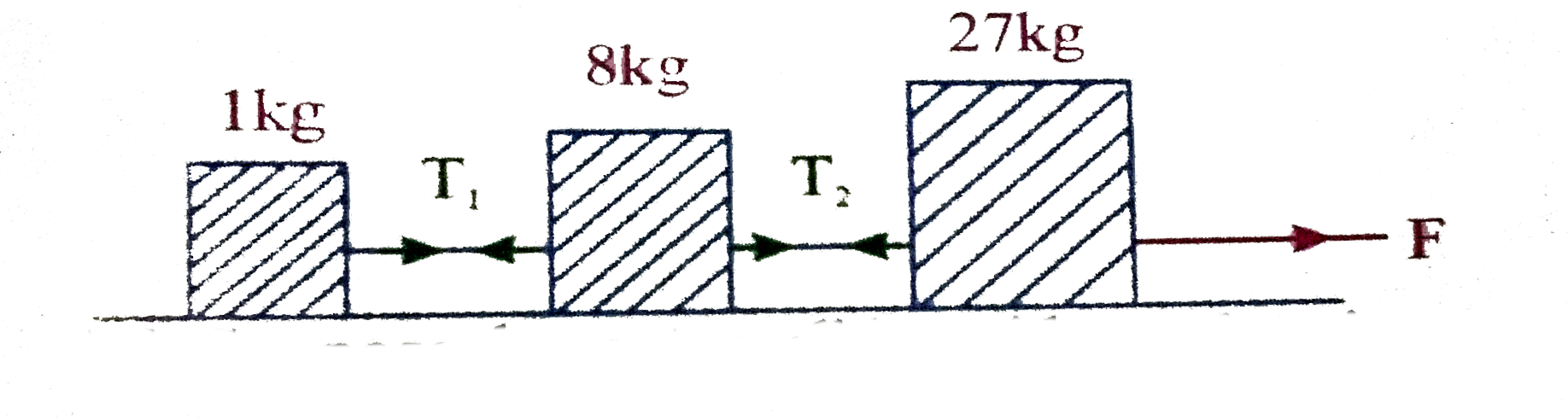 .View Solution
.View SolutionThree blocks A , B and C of masses 4kg , 2kg and 1kg respectively are in contact on a frictionless surface, as shown. If a force of 14Nisappliedonthe4kgblock,thenthecontactforcebetweenAandB is.
 View Solution
View Solution

