Three blocks of uniform thickness and masses m,mand2m are placed at the corners of a triangle having co-ordinates (2.5,1.5),(3.5,1.5)and(3,3) respectively. Find the co-ordinates of the centre of mass of the system.
To find the coordinates of the center of mass of the system of three blocks placed at the corners of a triangle, we can follow these steps:
Step 1: Identify the coordinates and masses
The coordinates of the three blocks and their respective masses are:
- Block 1: Mass = m, Coordinates = (2.5, 1.5)
- Block 2: Mass = m, Coordinates = (3.5, 1.5)
- Block 3: Mass = 2m, Coordinates = (3, 3)
Step 2: Write down the formula for the center of mass
The coordinates of the center of mass (CM) for a system of particles can be calculated using the formula:
xCM=∑mixi∑mi
yCM=∑miyi∑mi
where mi is the mass of each particle and xi,yi are the coordinates of each particle.
Step 3: Calculate the total mass
The total mass M of the system is:
M=m+m+2m=4m
Step 4: Calculate the x-coordinate of the center of mass
Using the coordinates and masses:
xCM=m⋅2.5+m⋅3.5+2m⋅34m
=2.5m+3.5m+6m4m
=12m4m=3
Step 5: Calculate the y-coordinate of the center of mass
Now, calculate the y-coordinate:
yCM=m⋅1.5+m⋅1.5+2m⋅34m
=1.5m+1.5m+6m4m
=9m4m=94
Step 6: Write the final coordinates of the center of mass
Thus, the coordinates of the center of mass of the system are:
(xCM,yCM)=(3,94)
Final Answer:
The coordinates of the center of mass are (3,94).
---
The coordinates of the three blocks and their respective masses are:
- Block 1: Mass = m, Coordinates = (2.5, 1.5)
- Block 2: Mass = m, Coordinates = (3.5, 1.5)
- Block 3: Mass = 2m, Coordinates = (3, 3)
The coordinates of the center of mass (CM) for a system of particles can be calculated using the formula:
xCM=∑mixi∑mi
yCM=∑miyi∑mi
where mi is the mass of each particle and xi,yi are the coordinates of each particle.
The total mass M of the system is:
M=m+m+2m=4m
Using the coordinates and masses:
xCM=m⋅2.5+m⋅3.5+2m⋅34m
=2.5m+3.5m+6m4m
=12m4m=3
Now, calculate the y-coordinate:
yCM=m⋅1.5+m⋅1.5+2m⋅34m
=1.5m+1.5m+6m4m
=9m4m=94
Thus, the coordinates of the center of mass of the system are:
(xCM,yCM)=(3,94)
The coordinates of the center of mass are (3,94).
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE
69 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE B
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - FILL IN THE BLANKS
20 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Three bodies of masses m, 2m and 3m are placed at the corners of a triangle having coordinates (1, 1.5), (2.5, 1.5) and (3, 3) respectively. Calculate the coordinates of the centre of mass.
View SolutionThree point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View Solution
Knowledge Check
The vertices of a triangle are (2, 1), (5, 2) and (3, 4). Then the co-ordinates of the centroid are
A10,3B(103,7)C(103,73)D(73,103)A system consists of 3 particles each of mass 'm' are located at (1, 1) (2, 2) and (3, 3). The co-ordinates of the centre of mass are
A(6, 6)B(2, 2)C(3, 3)D(1, 1)Particles of masses 3 kg, 4 kg, 5 kg nd 2 kg are placed at points A(3,2),B(−2,2),C(−2,−3) and D(1,−2) respectively of a co-ordinate system. The centre of mass of the system is at
A(−12,−12)B(−12,−514)C(0,−12)D(0,0)
The coordinates of the positions of particles of mass 7, 4 and 10 gm are (1, 5,-3) , (2, 5, 7) and (3, 3,-1) respectively. Find the position of the centre of mass of the system?
View SolutionPoint P is mid-point of the line segment AB. The co-ordinates of P and B are (3,1) and (5,-4) respectively. Find the co-ordinates of A
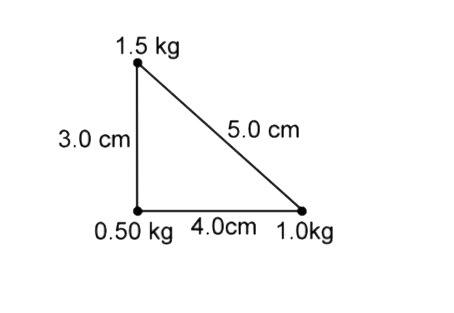
View SolutionThree particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
View SolutionIf three point masses m1,m2andm3 are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View SolutionThe co-ordinates of the end points of a diameter are (-1, 5) and (3, -1). Find the co-ordinates of the centre and the radius of circle.
View Solution