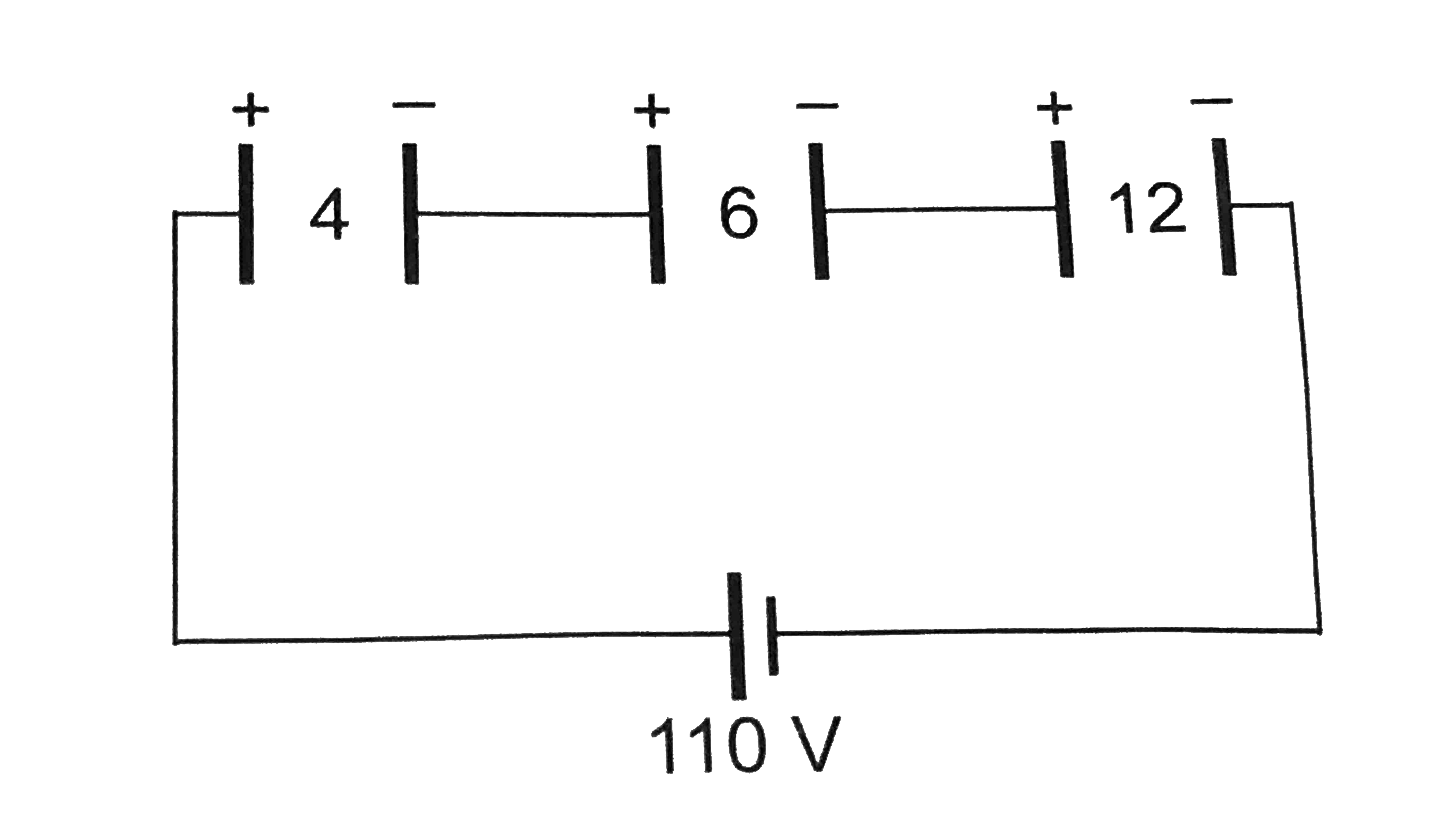
Three capacitors of capacitances $4 μ F, 6 μ F$ and $12 μ F$ are connected in series with a $110 V$ battery. The battery is disconnected,the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors arter the reconnection.

Video Solution

Text Solution

Verified by Experts

Before:
The equivalent capacitance
$\frac{1}{C_{e q}} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} = \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = \frac{3 + 2 + 1}{12} = \frac{1}{2}$
$C_{e q} = 2 μ F$
In series, charge on each capacitor is same
$Q_{1} = Q_{2} = Q_{3} = C_{e q} V = 2 \times 100 = 220 μ C$
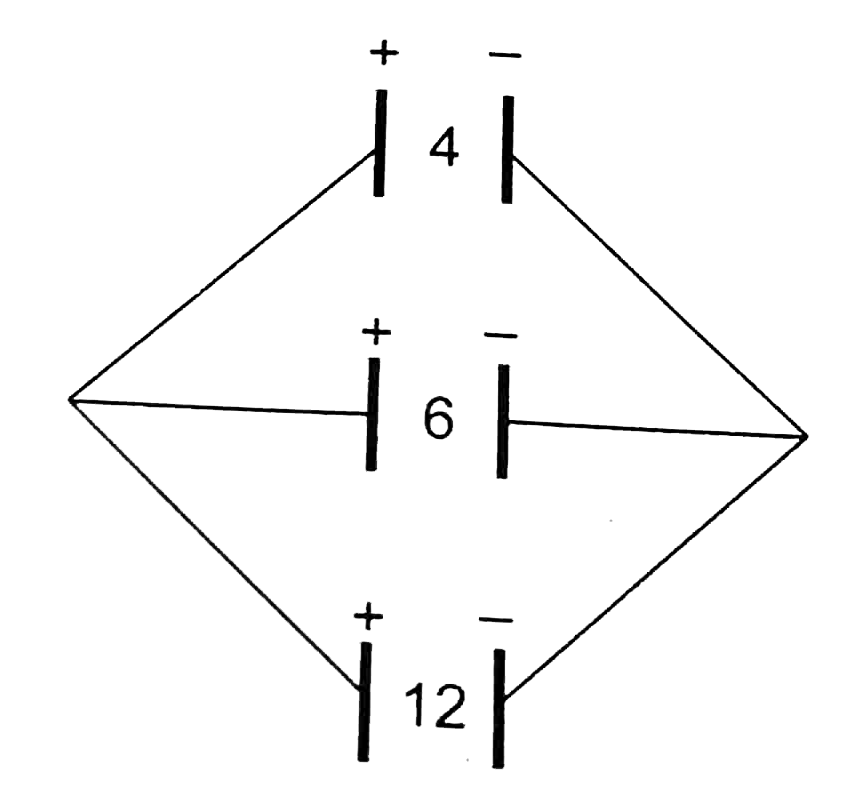
After reconnection:
Common potential:
$V = \frac{Q_{1} + Q_{2} + Q_{3}}{C_{1} + C_{2} + C_{3}} = \frac{3 \times 220}{4 + 6 + 12} = 30 V$
Final charges on capacitors:
$Q'_{1} = C_{1} V = 4 \times 30 = 120 μ C$
$Q'_{1} = C_{2} V = 6 \times 30 = 180 μ C$
$Q'_{1} = C_{3} V = 12 \times 30 = 360 μ C$

Updated on:21/07/2023

Three capacitors of capacitances $2 μ F$ , $3 μ F$ and $6 μ F$ are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
A $Q_{1} = \frac{7}{11} μ C, Q_{2} = \frac{10}{11} μ C and Q_{3} = \frac{21}{11} μ C$
B $Q_{1} = \frac{72}{11} μ C, Q_{2} = (\frac{18}{11} μ C and Q_{3} = \frac{216}{11} μ C$
C $Q_{1} = \frac{72}{11} μ C, Q_{2} = \frac{108}{11} μ C and Q_{3} = \frac{216}{11} μ C$
D $Q_{1} = \frac{2}{11} μ C, Q_{2} = \frac{108}{11} μ C and Q_{3} = \frac{216}{11} μ C$
Two capacitors A and B having capacitances $10 μ f$ and $20 μ F$ are connected in series with a 12 V battery. The ratio of the charge on A and B is
A $0.5 : 1$
B $1 : 1$
C $2 : 1$
D $2 : 4$
Three capacitors of capacitance $3 μ F, 10 μ F$ and $15 μ F$ are connected in series to a voltage source of $100 V$ . The charge on $15 μ F$ is
A $50 μ C$
B $100 μ C$
C $200 μ C$
D $280 μ C$