Three charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
−q
−2q
−q2
q
The correct Answer is:1
To find the value of charge Q such that the net force on charge q is zero, we can follow these steps:
Step 1: Identify the positions of the charges
- Charge q is located at position 0.
- Charge Q is located at position L2.
- Charge −4q is located at position L.
Step 2: Determine the forces acting on charge q
- The force on charge q due to charge Q (located at L2) will be attractive if Q is negative and repulsive if Q is positive.
- The force on charge q due to charge −4q (located at L) will always be attractive since it is negative.
Step 3: Calculate the force between q and Q
The force FqQ between charges q and Q is given by Coulomb's law:
FqQ=14πϵ0|q⋅Q|(L2)2=14πϵ04|q⋅Q|L2
Step 4: Calculate the force between q and −4q
The force Fq(−4q) between charges q and −4q is:
Fq(−4q)=14πϵ0|q⋅(−4q)|(L−0)2=14πϵ04q2L2
Step 5: Set the forces equal for equilibrium
For the net force on charge q to be zero, the magnitudes of the forces must be equal:
FqQ=Fq(−4q)
Substituting the expressions we derived:
4|q⋅Q|4πϵ0L2=4q24πϵ0L2
This simplifies to:
|Q|=q
Step 6: Determine the sign of Q
Since FqQ must be attractive (to counteract the attractive force from −4q), Q must be negative:
Q=−q
Conclusion
Thus, the charge Q must be equal to −q in order to make the net force on q zero.
- Charge q is located at position 0.
- Charge Q is located at position L2.
- Charge −4q is located at position L.
- The force on charge q due to charge Q (located at L2) will be attractive if Q is negative and repulsive if Q is positive.
- The force on charge q due to charge −4q (located at L) will always be attractive since it is negative.
The force FqQ between charges q and Q is given by Coulomb's law:
FqQ=14πϵ0|q⋅Q|(L2)2=14πϵ04|q⋅Q|L2
The force Fq(−4q) between charges q and −4q is:
Fq(−4q)=14πϵ0|q⋅(−4q)|(L−0)2=14πϵ04q2L2
For the net force on charge q to be zero, the magnitudes of the forces must be equal:
FqQ=Fq(−4q)
Substituting the expressions we derived:
4|q⋅Q|4πϵ0L2=4q24πϵ0L2
This simplifies to:
|Q|=q
Since FqQ must be attractive (to counteract the attractive force from −4q), Q must be negative:
Q=−q
Thus, the charge Q must be equal to −q in order to make the net force on q zero.
Topper's Solved these Questions
Similar Questions
Three charges -q,+2q, and -q are arranged on a line as shown in fig. Calculate the field at a distance rgtgta on the line.
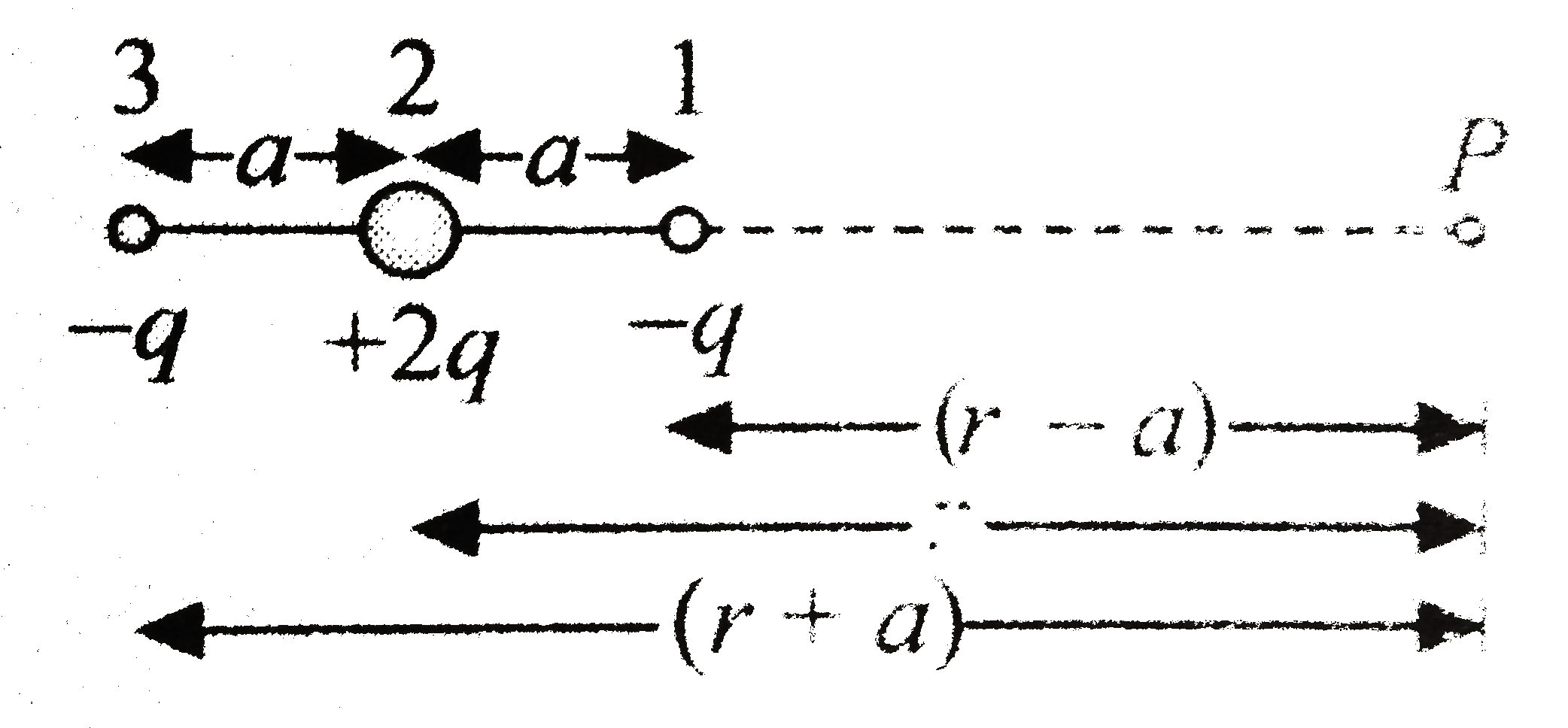
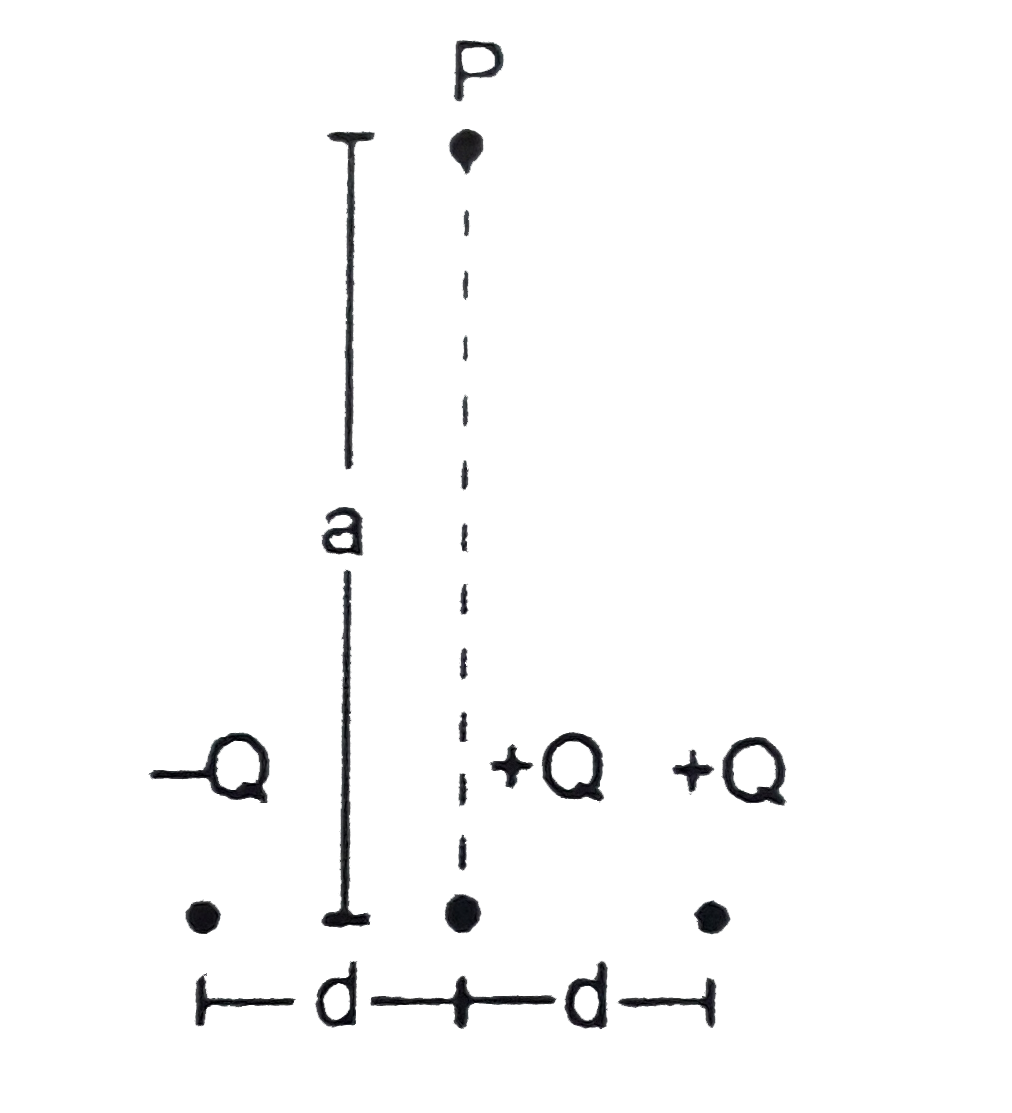
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.
View Solution
Knowledge Check
Three charges 4q,Q and q are in a straight line in the position of 0.l/2 and l respectively. The resultant force on q will be zero, if Q=
A−qB−2qC−q2D4qThree charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ isA2B5.5C4D1.5Three point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
A4Q and 16Q must be at the ends and Q at a distance of 3 cm from the 16QB4Q and 16Q must be at the ends and Q at a distance of 3 cm from the 16QCElectric field at the position of Q at a distance of 6cm from the 16Q.DElectric field at the position of Q at a distance of 6cm from the 16Q.
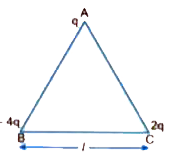
Three point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
View SolutionThree charges -q, +q and -q are placed along a st. line at equal distance , say a. Calculated the potential energy of this system of charges (i) when +q charge is in the middle and (ii) when this charge is at one end.
View SolutionThree point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionThree charge +Q,+Q and −Q are placed at the corners of an equilateral triangle. The ratio of the force on a positive charge to the force on the negative charge will be equal to
View Solution
