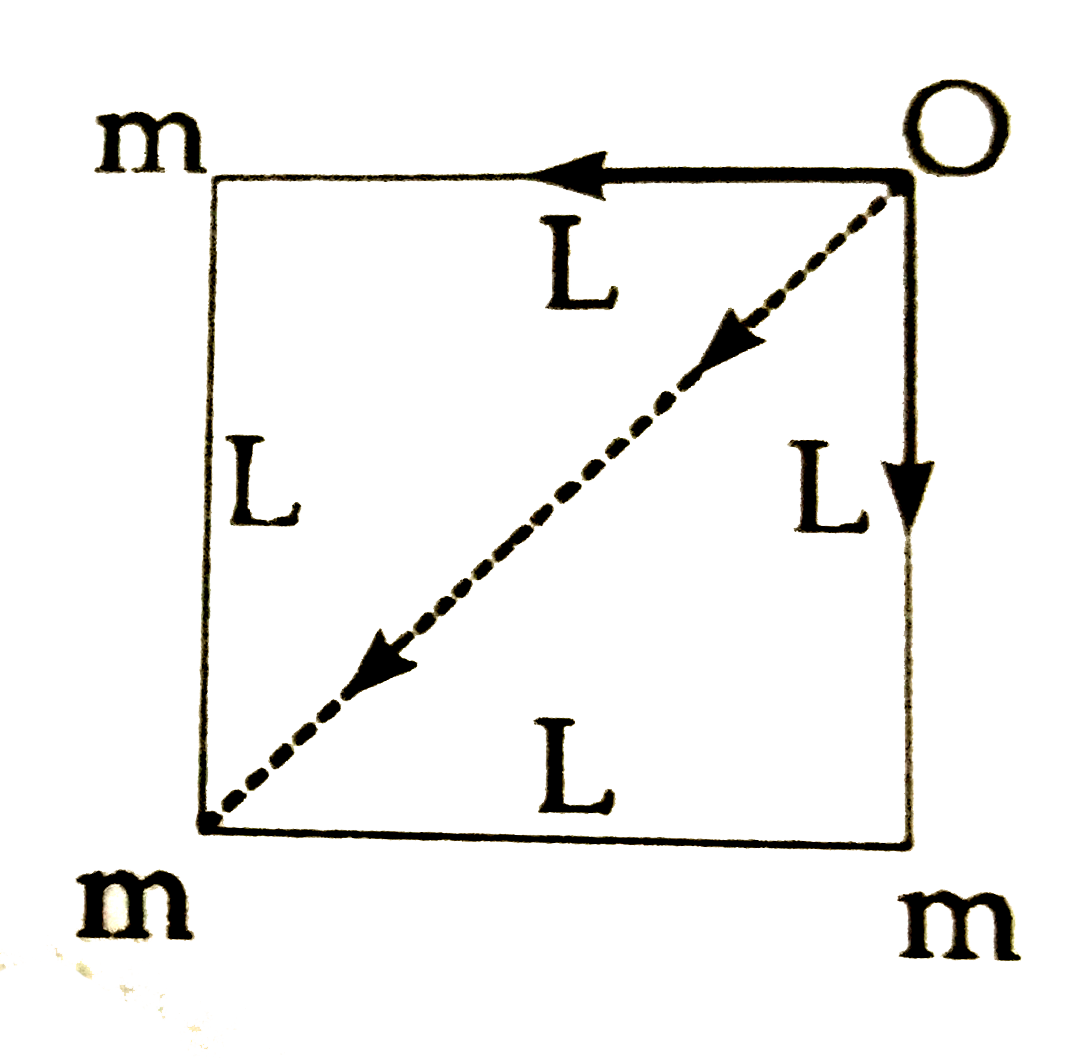
Three equal point masses of each mass m are located, respectively at three corners of a square of edge length l as shown in figure. The magnitude of intensity of gravitational field (g) at the fourth corner due to these masses is
Gml2(√2+22)
2Gml2(1+√2)√2
Gml2(2√2+12)
Gml2√2+12
The correct Answer is:c
E1=GMl2,E2=GMl2,andE3=GM2l2
ER=√(E21+E22)
=√(GMl2)2+(GMl2)=√2(GMl2)
E'R=ER+E3=GMl2(√2+12)
Topper's Solved these Questions
Similar Questions
Four particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionThree point charges are kept at the three corners of an equilateral triangle of edge length a, as shown in the figure. The net electric dipole moment of the system is

View Solution
Knowledge Check
If three point charges are placed at the three corners of a square of diagonals 2a as shown in figure. Then ∫AB→E.→dr will be -
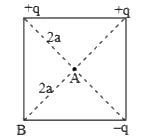 Aq4πε0aB−q8πε0aC−q4πε0aDq8πε0a
Aq4πε0aB−q8πε0aC−q4πε0aDq8πε0aSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
A6Gm2a2B6Gmm0a2CzeroD6Gma4
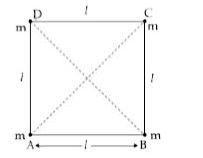
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be:
View SolutionThree point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .
.
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

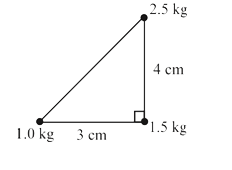
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
View SolutionFour particles A,B,CandD of masses m,2m,3mand4m respectively are placed at corners of a square of side x as shown in Fig.

Locate the centre of mass.
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View Solution
