Three idential spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
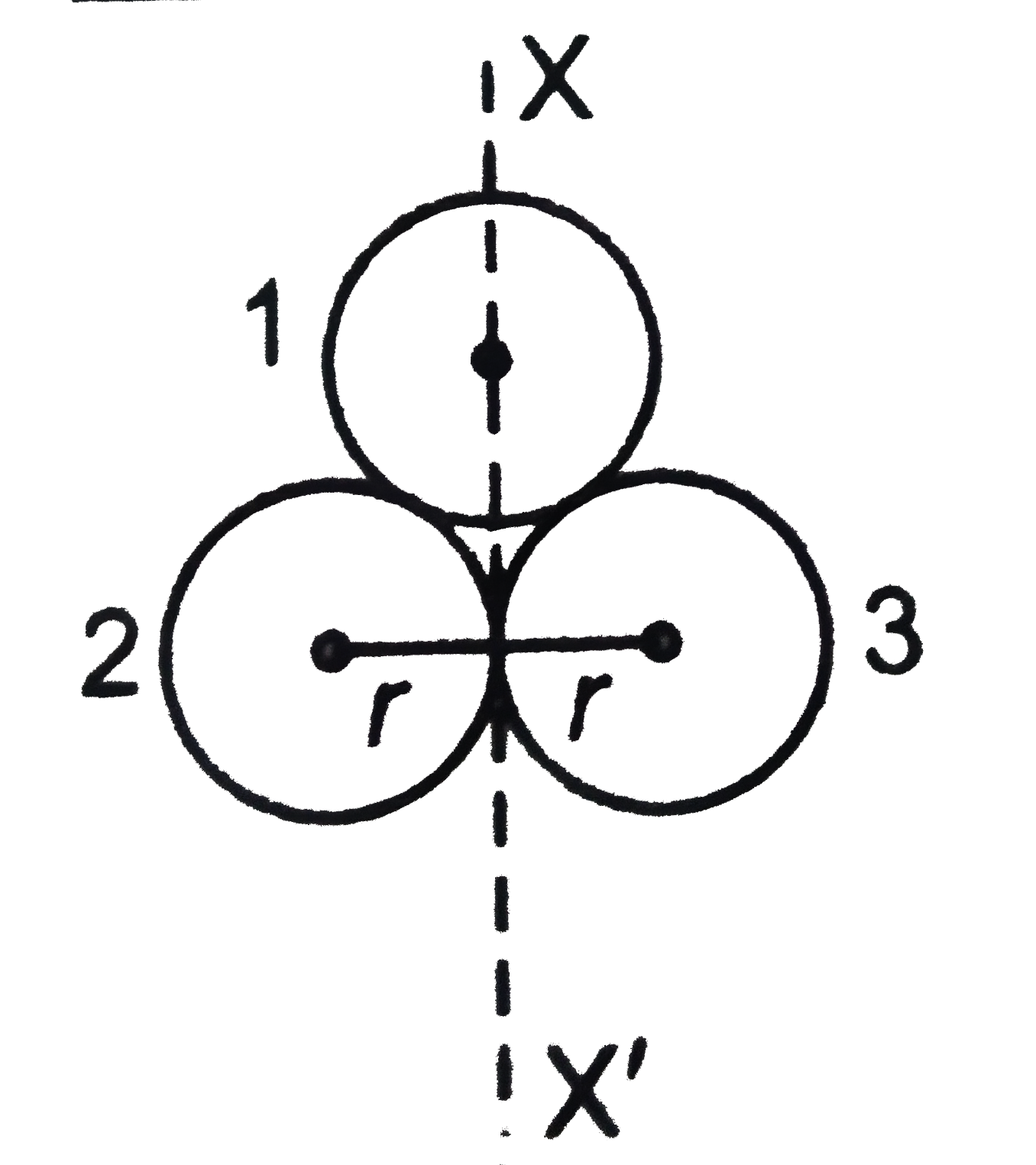
115mr2
3mr2
165mr2
4mr2
The correct Answer is:D
The total moment of inertia of the system is
I=I1+I2+I3...(i)
Here, I1=23mr2
I2=I3=23mr2+mr2 (From parallel axis theorem)
=53mr2
From Eq. (i),
I=23mr2+2×53mr2=mr2(23+103)⇒I=4mr2.
Topper's Solved these Questions
Similar Questions
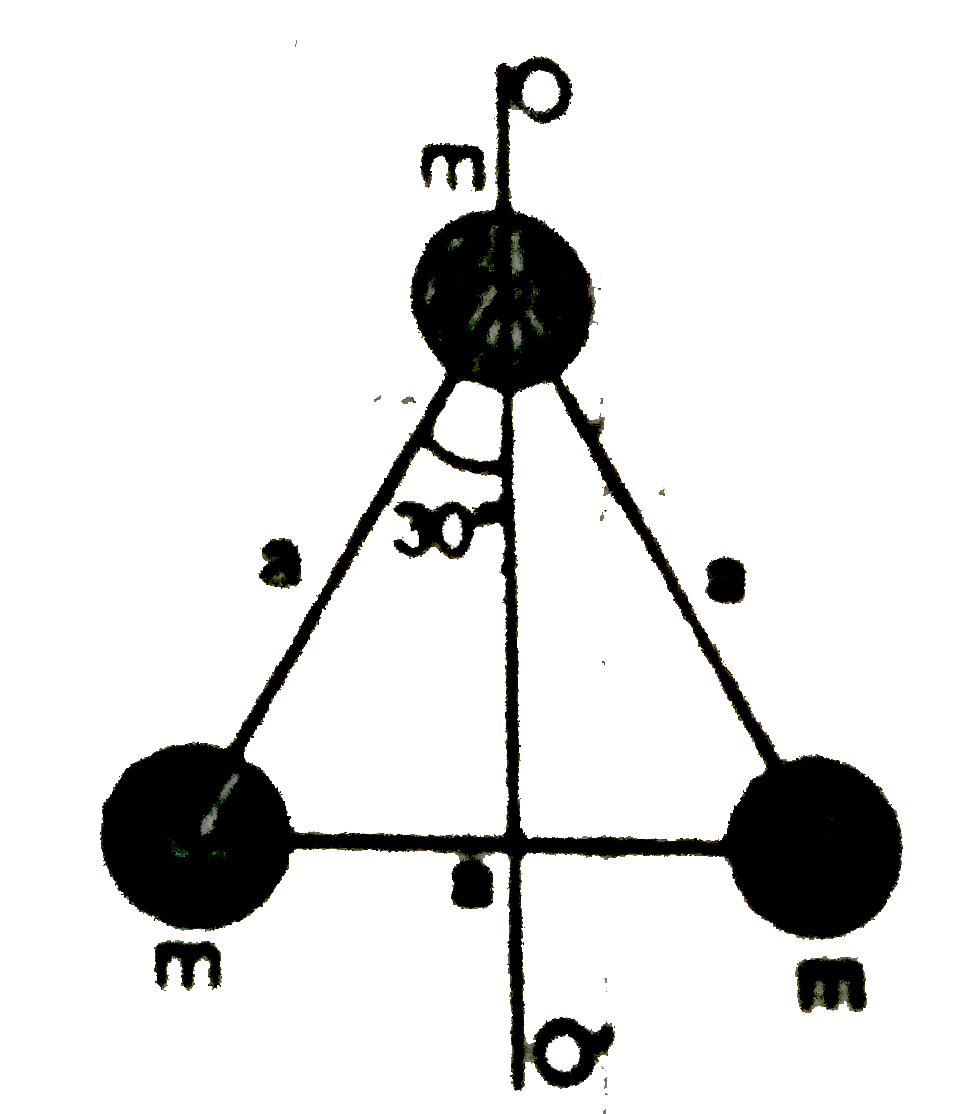
Three point masses are arranged as shown in the figure. Moment of inertia of the system about the axis OO' is
View SolutionThree identical rings of masses m each and radius r are kept in contact as shown in Fig. Find the moment of inertia of the system about a common tangent.
View SolutionThree spherical shells of masses M, 2M and 3M have radii R, 3R and 4R as shows in figure. Find net potential at point P,
View SolutionDerive an expression for the moment of inertia of a thin spherical shell about a diameter.
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionTwo identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is

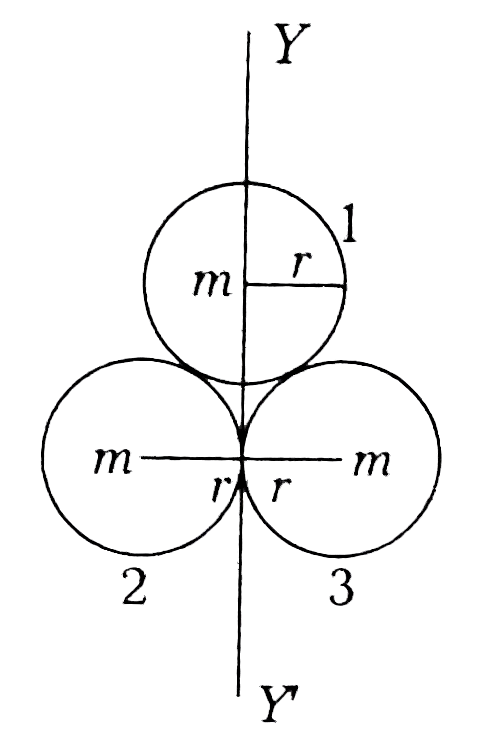
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View Solution
