Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
1.67×10−9(ˆi+ˆj)N
3.34×10−10(ˆi+ˆj)N
1.67×10−9(ˆi−ˆj)N
3.34×10−10(ˆi+ˆj)N
The correct Answer is:A
To solve the problem of finding the net gravitational force on the mass at the origin due to the other two masses, we can follow these steps:
Step 1: Identify the positions of the masses
We have three identical point masses, each with a mass of 1 kg, located at:
- Mass A at (0, 0) (the origin)
- Mass B at (0, 0.2 m)
- Mass C at (0.2 m, 0)
Step 2: Calculate the gravitational force exerted on the mass at the origin by Mass B
The gravitational force F between two point masses is given by the formula:
F=G⋅m1⋅m2r2
Where:
- G=6.67×10−11N m2/kg2 (gravitational constant)
- m1=1kg (mass at the origin)
- m2=1kg (mass B)
- r is the distance between the two masses, which is 0.2m.
Calculating the force due to Mass B:
FB=6.67×10−11⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
This force acts in the negative y-direction (downward).
Step 3: Calculate the gravitational force exerted on the mass at the origin by Mass C
Now, we calculate the gravitational force exerted by Mass C:
- The distance r between the mass at the origin and Mass C is also 0.2m.
Calculating the force due to Mass C:
FC=6.67×10−11⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
This force acts in the negative x-direction (to the left).
Step 4: Determine the net gravitational force on the mass at the origin
The net gravitational force →Fnet on the mass at the origin is the vector sum of the forces due to Mass B and Mass C:
→Fnet=→FB+→FC
Expressing this in vector form:
→Fnet=−1.6675×10−9^j−1.6675×10−9^i
Step 5: Final Result
Thus, the net gravitational force on the mass at the origin is:
→Fnet=−1.6675×10−9^i−1.6675×10−9^jN
We have three identical point masses, each with a mass of 1 kg, located at:
- Mass A at (0, 0) (the origin)
- Mass B at (0, 0.2 m)
- Mass C at (0.2 m, 0)
The gravitational force F between two point masses is given by the formula:
F=G⋅m1⋅m2r2
Where:
- G=6.67×10−11N m2/kg2 (gravitational constant)
- m1=1kg (mass at the origin)
- m2=1kg (mass B)
- r is the distance between the two masses, which is 0.2m.
FB=6.67×10−11⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
Now, we calculate the gravitational force exerted by Mass C:
- The distance r between the mass at the origin and Mass C is also 0.2m.
FC=6.67×10−11⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
The net gravitational force →Fnet on the mass at the origin is the vector sum of the forces due to Mass B and Mass C:
→Fnet=→FB+→FC
Expressing this in vector form:
→Fnet=−1.6675×10−9^j−1.6675×10−9^i
Thus, the net gravitational force on the mass at the origin is:
→Fnet=−1.6675×10−9^i−1.6675×10−9^jN
Topper's Solved these Questions
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Field And Acceleration Due To Gravity
34 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Gravitational Potential, Energyand Escape Velocity
32 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View Solution
Knowledge Check
The centre of mass of three bodies each of mass 1 kg located at the points (0,0), (3, 0) and (0, 4) in the x-y plane is
A(43,1)B(13,23)C(12,12)D(1,43)A large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
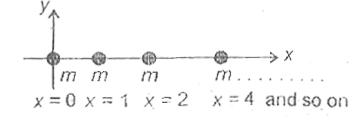 AGm2B43Gm2C23Gm2D54Gm2
AGm2B43Gm2C23Gm2D54Gm2An equation of the plane through the points (1,0,0), (0,2,0) and at a distance 6/7 units from the origin, is
A6x+3y+z−6=0B6x+3y+2z−6=0C6x+3y+z+6=0D6x+3y+2z+6+0
Three point masses of 1kg,2kgand3kg lie at (1,2),(0,−1)and(2,−3) respectively. Calculate the co-ordinates of the centre of mass of the system.
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View SolutionFour identical masses m each are kept at points A, B, C & D shown in figure. Gravitational force on mass at point D (body centre) is -
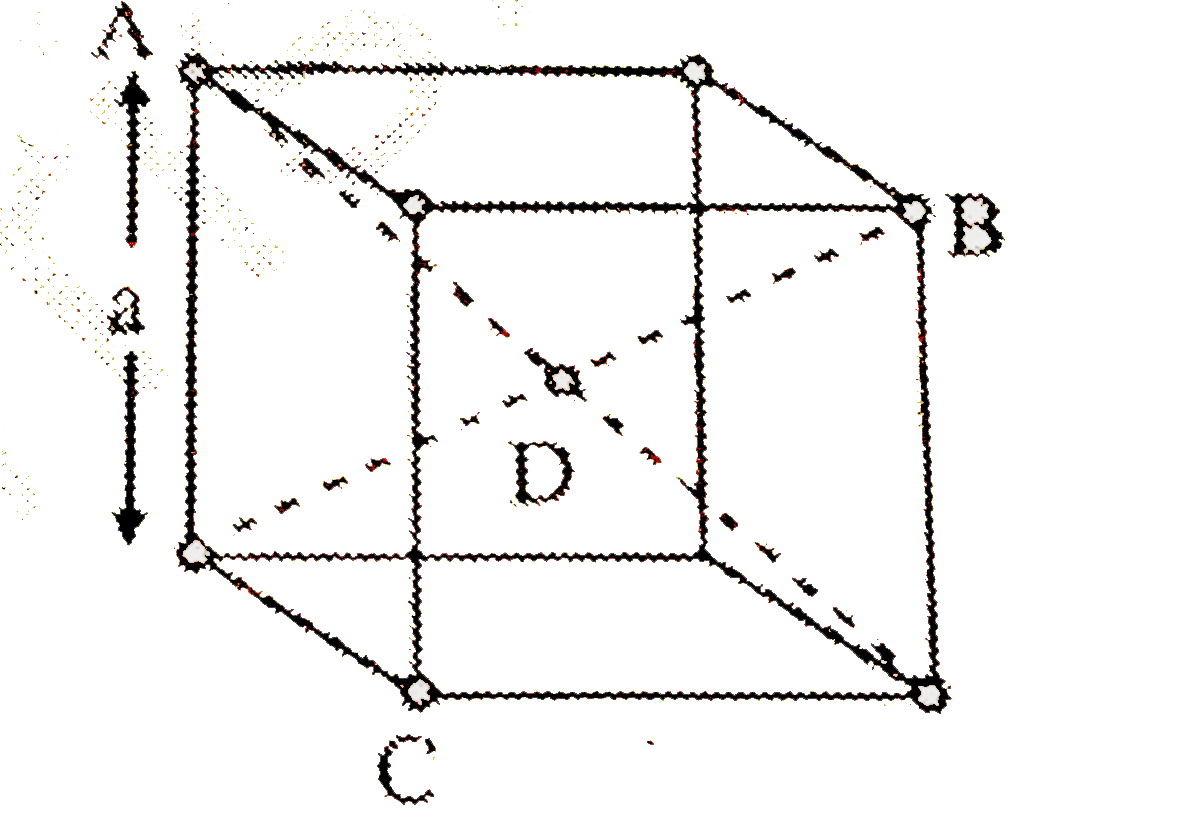
View Solution
