Three identical spherical shells each of mass m and radius r are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
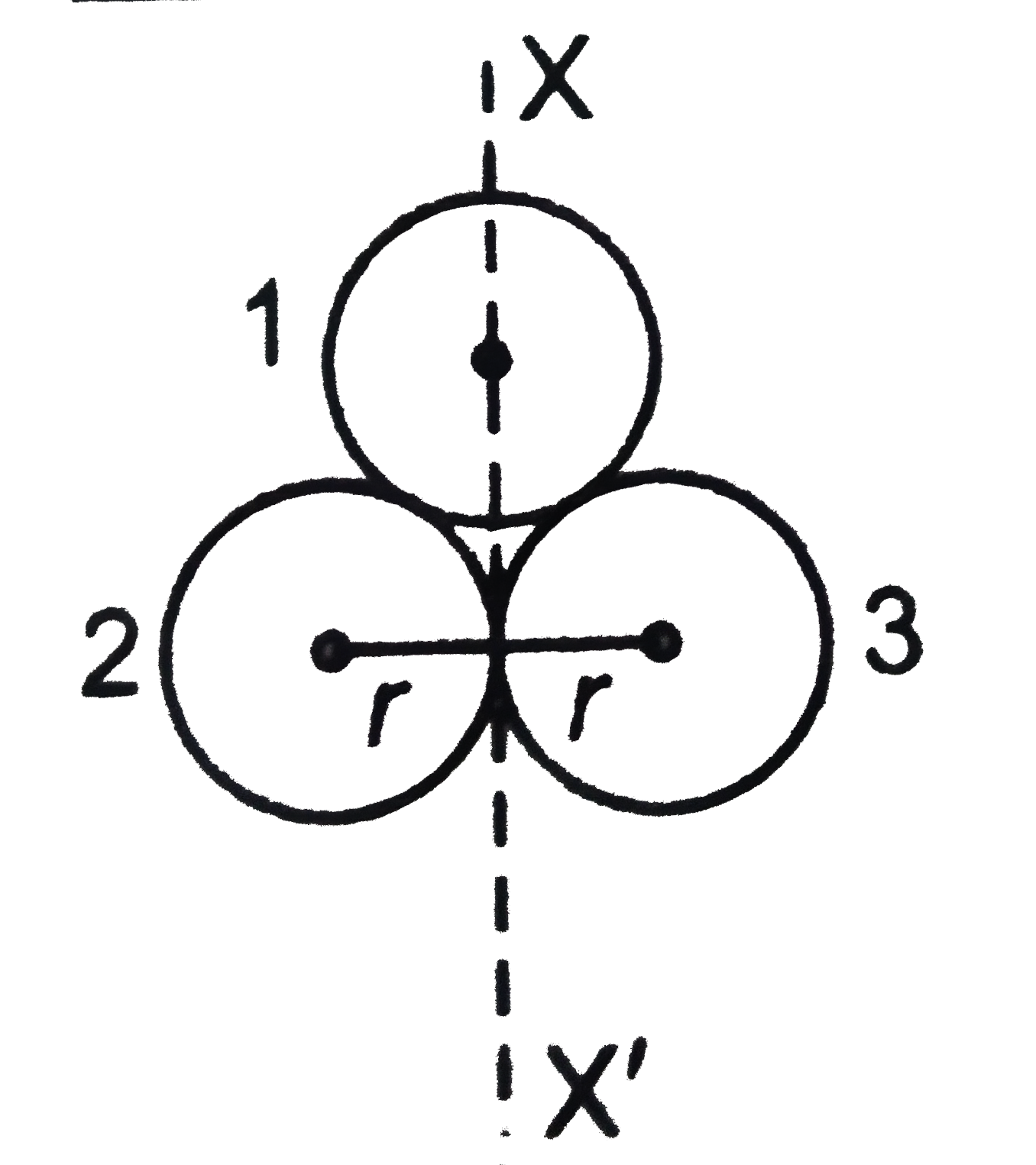
115mr2
3mr2
165mr2
4mr2
The correct Answer is:D
The total moment of inertia of the system is
I=I1+I2+I3...(i)
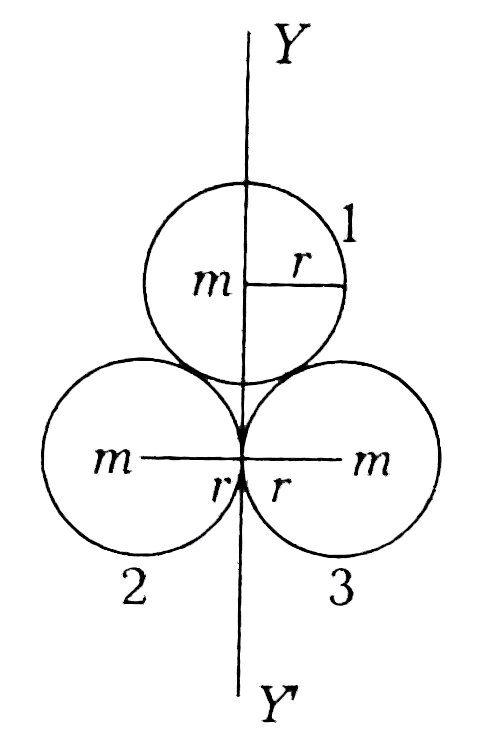
Here, I1=23mr2
I2=I3=23mr2+mr2 (From parallel axis theorem)
=53mr2
From Eq. (i),
I=23mr2+2×53mr2=mr2(23+103)⇒I=4mr2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
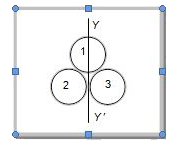 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
Athe particle will execute S.H.M inside the shellBthe particle will oscillate inside the shell, but the oscillations are not simple harmonicCthe particle will not oscillate, but the speed the particle will go on increasingDnone ot theseTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
A3MR2B32MR2C14MR2D2MR2
Three discs each of mass M and radius R are placed in contact with each other as shown in figure here. Then the MI of the system about an axis XX' is

View SolutionTwo identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure). The moment of inertia of the system about the axis passing perpendicularly through the centre of the rod is

View SolutionTwo identical circular plates each of mass M and radius R are attached to each other with their planes ⊥r to each other. The moment of inertia of system about an axis passing through their centres and the point of contact is
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
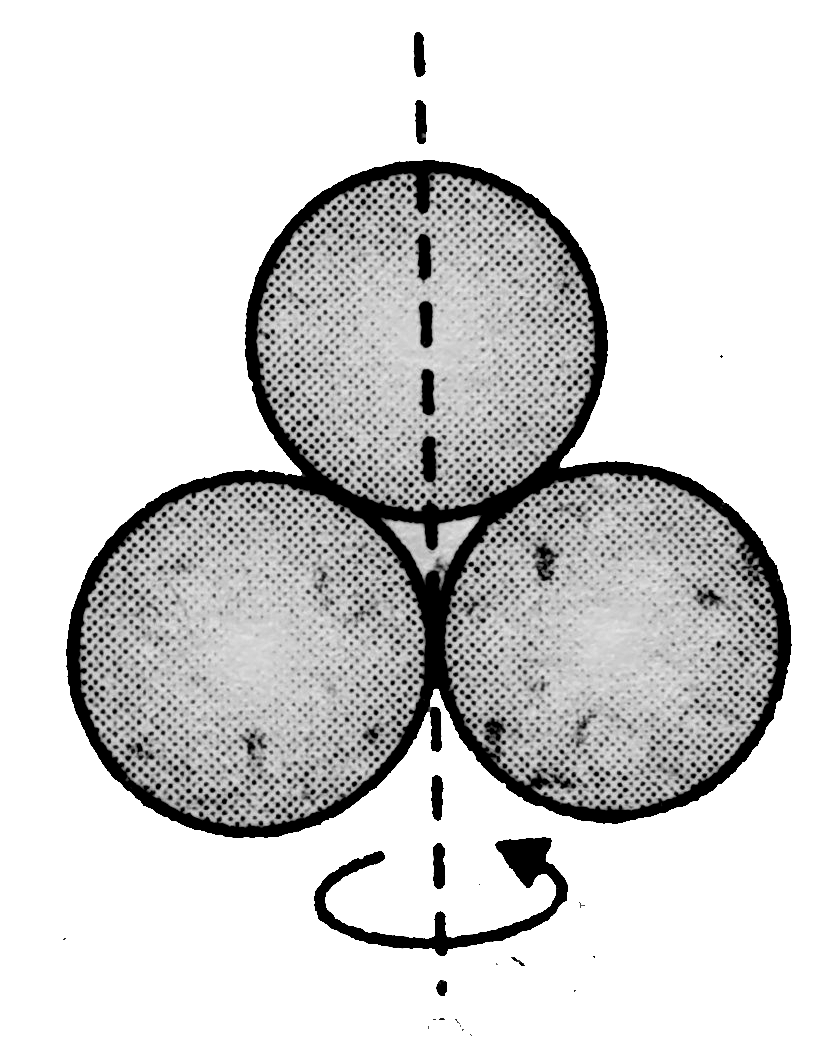
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
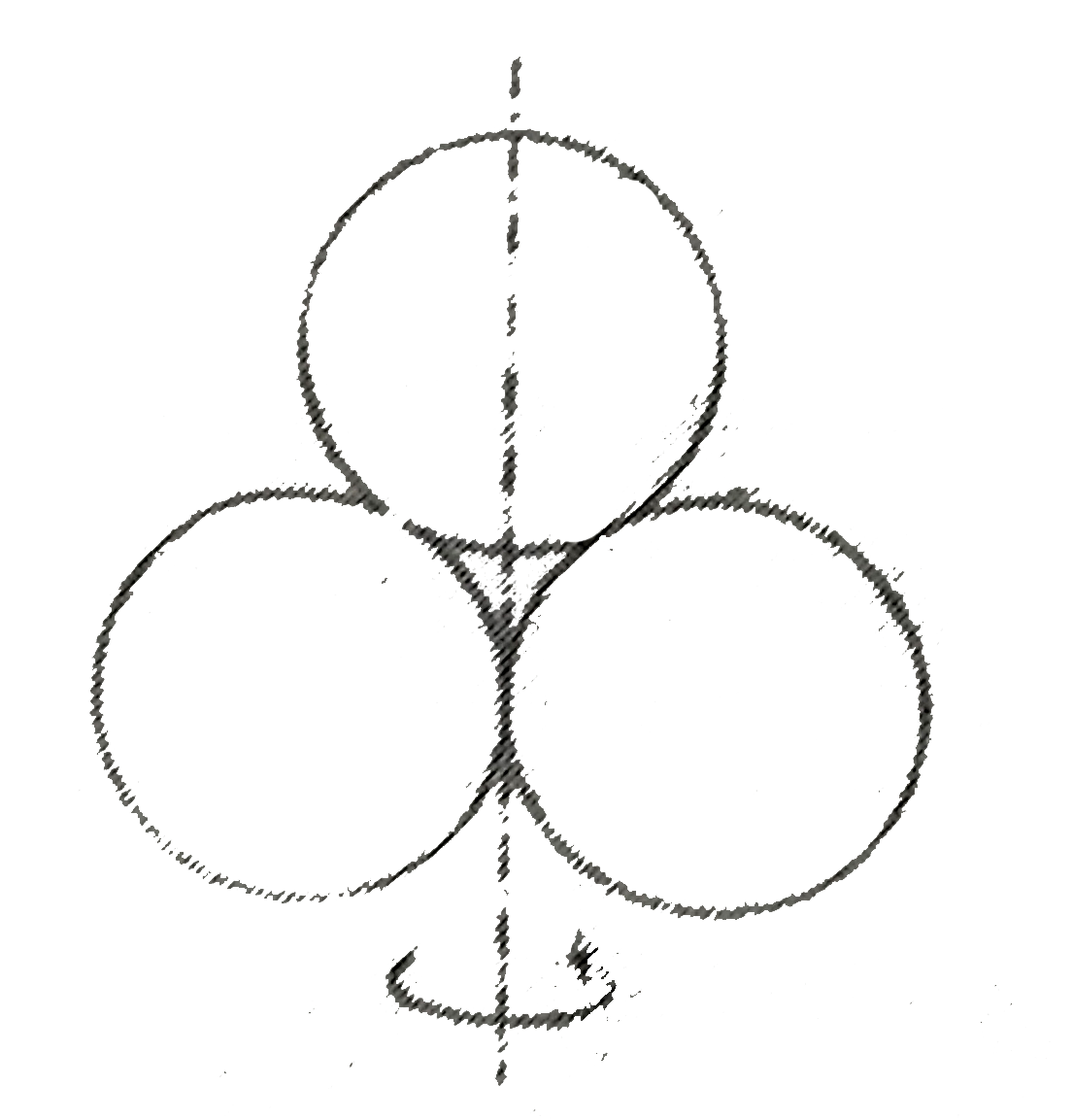
View Solution

