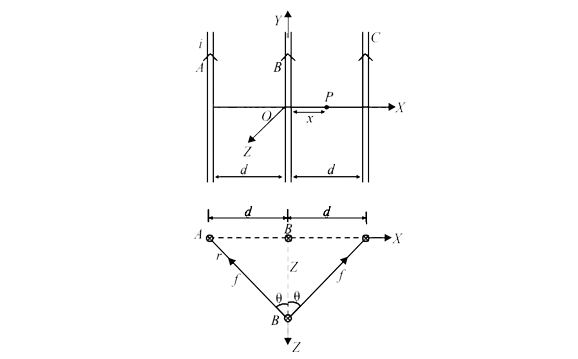
Three infinitely long thin wires, each carrying current $i$ in the same direction, are in the $x - y$ plane of a gravity free space . The central wire is along the $y - a ξ s$ while the other two are along $x = \pm d$ .
(i) Find the locus of the points for which the magnetic field $B$ is zero.
(ii) If the central wire is displaced along the $Z - d i r e c t i o n$ by a small amount and released, show that it will excecute simple harmonic motion . If the linear density of the wires is $λ$ , find the frequency of oscillation.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(i) KEY CONCEPT : Magnetic field due to an infinitely long current carrying wire at distance $r$ is given by
$B = \frac{μ_{0}}{4 π} (\frac{2 i}{r})$
The direction of $B$ is given by right hand palm rule. Hence , in case of three identical wires , resultant field can be zero only if the point $P$ is between the two wires , otherwise $B$ due to all the wires will be in the same direction and so resultant $B$ cannot be zero. Hence , if point $P$ is at a distance $x$ from the central wire as shown in figure , then, ${\to B}_{p} = {\to B}_{P A} + {\to B}_{P C}$
where ${\to B}_{P A} = m a g \neq t i c f i e l d a t p d u e \to A$
${\to B}_{P B} = m a g \neq t i c f i e l d a t P d u e \to B$
${\to B}_{P C} = m a g \neq t f i e l d a t P d u e \to C$ .
${\to B}_{P} = \frac{μ_{0}}{4 π} [\frac{1}{d + x} + \frac{1}{x} - \frac{1}{d - x}] (- ˆ K)$ .
For ${\to B}_{P} = 0$ , we get $x = \pm \frac{d}{\sqrt{3}}$
(ii) KEY CONCEPT : the force per unit length between two parallel current carrying wires is given by
$\frac{μ_{0}}{4 π} \frac{2 i_{1} i_{2}}{r} = f (s a y)$
and i9s attractive if currents are in the same direction . ltbr> So , when the wire $B$ is diplaced along $Z - a ξ s$ by a small distance $Z$ , the restoring force per unit length $\frac{F}{l}$ on the wire $B$ due to wires $A and C$ will be
$\frac{F}{l} = 2 f cos θ = 2 \frac{μ_{0}}{4 π} \frac{2 i_{1} i_{2}}{r} \times \frac{z}{r} [a s cos θ = \frac{z}{r}]$
or (F)/(l) = mu_(0) /( 4pi) . ( 4i^(2) z)/(( d^(2) + z^(2))) [ as I_(1) I_(2) and r^(2) = d^(2) + z^(2)] $< b r > or \frac{F}{l} = \frac{μ_{0}}{4 π} \frac{2 i}{d})^{2} z [a s d > > z and F i s o p p o s i t e \to z]$ .... (i)
Since $F \propto - z$ , the motion is simple harmonic.
Comparing eq. (i) with the standard equation of $S . H . M .$ which is
$F = - m ω^{2} z i . e ., \frac{F}{l} = - \frac{m}{l} ω^{2} z$ $= - λ ω^{2} z$ , we get
$λ ω^{2} = \frac{μ_{0}}{4 π} \times \frac{4 i^{2}}{d^{2}} \Rightarrow ω = \sqrt{\frac{μ_{0} i^{2}}{π d^{2} λ}}$
$2 π n = \frac{i}{d} \sqrt{\frac{μ_{0}}{π λ}} \Rightarrow n = \frac{i}{2 π d} \sqrt{\frac{μ_{0}}{π λ}}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

A $\frac{μ_{0} I}{π r}$
B $\frac{μ_{0} I}{r} (\frac{1}{π} + \frac{1}{4})$
CZero
D $\frac{μ_{0} I}{2 π r}$
Question 2 - Select One
Two infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wires
Bhalf of the magnetic field produced due to each of the wires
Ctwice the magnetic field produced due to each of the wires
Dzero
Question 3 - Select One
Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wires
BHalf of the magnetic field produced due to each of the wires
CSquare of the magnetic field produced due to each of the wires
DZero

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-MOVING CHARGES AND MAGNETISM-MCQs(d )

Home
Ask Doubt
Profile