Three mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring. When is 0.4 kg mass is removed , the system oscillates with a period 2 s . When the 0.3 kg mass is also removed , the system will oscillates with a period
1 s
2 s
3 s
4 s
The correct Answer is:A
To solve this problem, we need to analyze the oscillation of the spring-mass system and how the removal of masses affects the period of oscillation. Let's break it down step by step.
Step 1: Understand the formula for the period of oscillation
The period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass attached to the spring and k is the spring constant.
Step 2: Analyze the first scenario
When the 0.4 kg mass is removed, the remaining mass is:
m1=0.1kg+0.3kg=0.4kg
Given that the period T1 is 2 seconds, we can write:
T1=2π√0.4k=2s
Step 3: Solve for the spring constant k
We can rearrange the equation to find k:
2=2π√0.4k
Dividing both sides by 2π:
1π=√0.4k
Squaring both sides:
1π2=0.4k
Thus,
k=0.4π2
Step 4: Analyze the second scenario
Now, when the 0.3 kg mass is also removed, the remaining mass is:
m2=0.1kg
We need to find the new period T2:
T2=2π√m2k=2π√0.10.4π2
Step 5: Simplify the expression for T2
Substituting k into the equation:
T2=2π√0.10.4π2=2π√0.10.4⋅1π
This simplifies to:
T2=2√0.10.4=2√14=2⋅12=1s
Final Answer
Thus, when the 0.3 kg mass is also removed, the system will oscillate with a period of:
1s
The period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass attached to the spring and k is the spring constant.
When the 0.4 kg mass is removed, the remaining mass is:
m1=0.1kg+0.3kg=0.4kg
Given that the period T1 is 2 seconds, we can write:
T1=2π√0.4k=2s
We can rearrange the equation to find k:
2=2π√0.4k
Dividing both sides by 2π:
1π=√0.4k
Squaring both sides:
1π2=0.4k
Thus,
k=0.4π2
Now, when the 0.3 kg mass is also removed, the remaining mass is:
m2=0.1kg
We need to find the new period T2:
T2=2π√m2k=2π√0.10.4π2
Substituting k into the equation:
T2=2π√0.10.4π2=2π√0.10.4⋅1π
This simplifies to:
T2=2√0.10.4=2√14=2⋅12=1s
Thus, when the 0.3 kg mass is also removed, the system will oscillate with a period of:
1s
Similar Questions
A 0.2kg of mass hangs at the end of a spring. When 0.002kg more mass is added to the end of the spring, it stretches 7 cm more. If the 0.02 kg mass is removed what will be the period of vibration of the system?
View SolutionA mass of 0.1 kg hangs at the end of a spring. When a mass of 0.01 kg more is added at the end of the spring, it stretches by 5 cm more. When the extra 0.01 kg mass is removed, determine the time period of vibration of the system.
View Solution
Knowledge Check
Three masses of 500g, 300g and 100g are suspended at the end of a spring as shown and are in equilibrium. When the 500g mass is removed suddenly, the system oscillates with a period of 2s. When the 300g mass is also removed, it will oscillate with period T. Find the value of T.
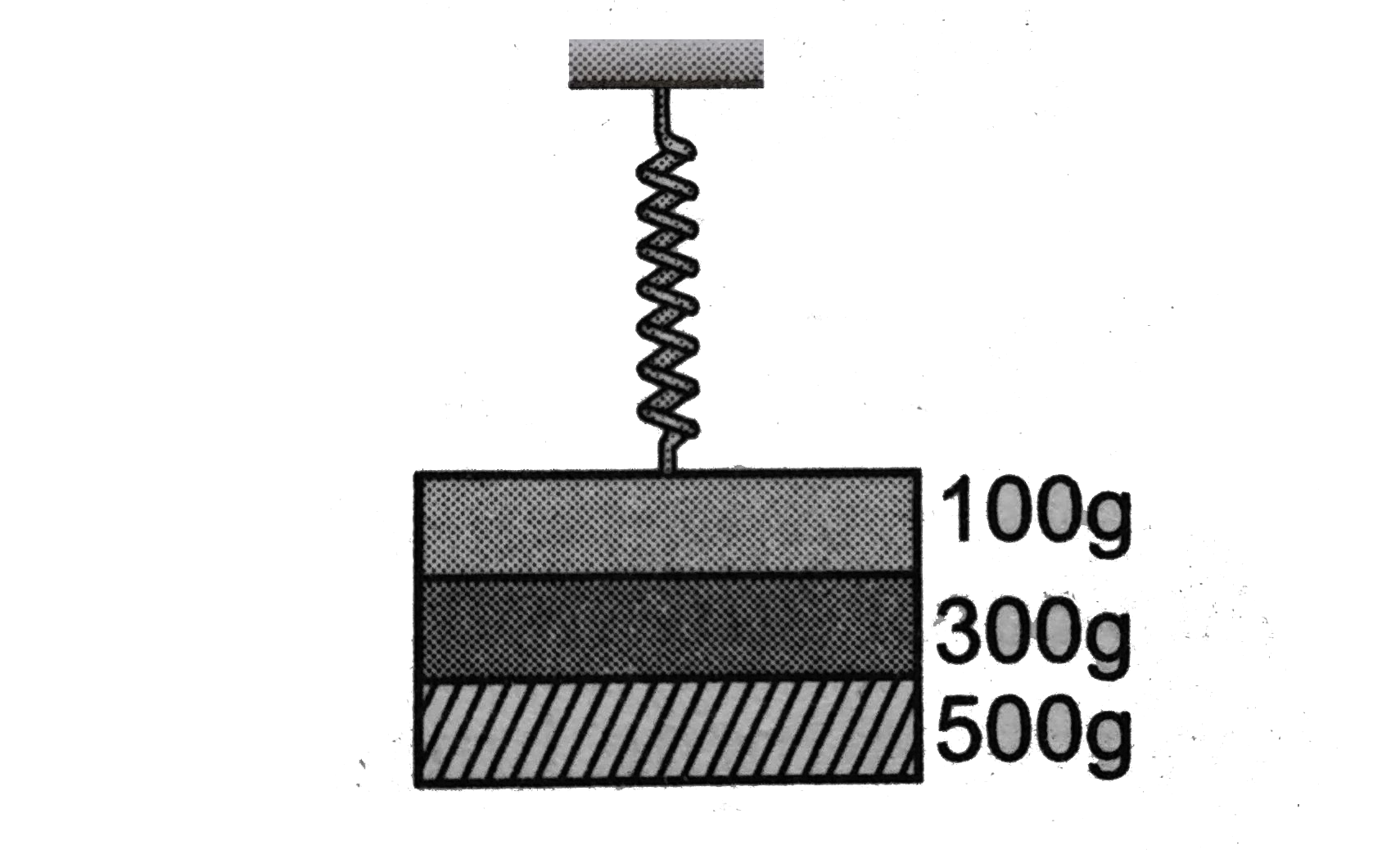 A1 sB2 sC3 sD4 s
A1 sB2 sC3 sD4 sThree masses 700g, 500g, and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillacts with a period of 3 seconds, when the 500 gm mass is also removed, it will oscillate with a period of
 A1 sB2 sC3 sD√125s
A1 sB2 sC3 sD√125sThree masses 700 g , 500 g , and 400 g are suspended at the end of a spring a shown and are in equilibrium. When the 700 g mass is removed, the system oscillates with a period of 3 seconds, when the 500 gm mass also removed. It will oscillate with a period of
 A1sB2 sC3 sD√125s
A1sB2 sC3 sD√125s
Three points masses 1.0 kg , 1.5 kg and 2.5 kg are placed at the vertices of a right-angle triangle of sides 4.0 cm, 3.0 cm and 5.0 cm, as shown in the figure. The centre of mass of the system is
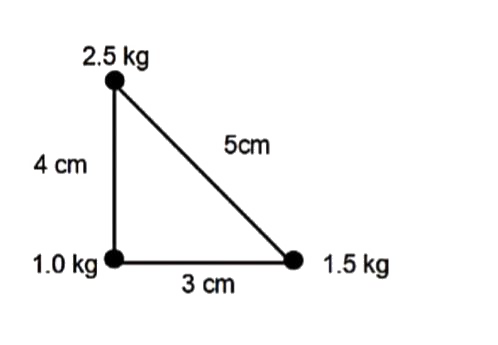
View SolutionA mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
View SolutionWhen a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
View SolutionA mass m attached to a spring oscillates with a period of 3s. If the mass is increased by 1kg the period increases by 1s. The initial mass m is
View SolutionA mass m attached to a light spring oscillates with a period of 2 s. If the mass is increased by 2 kg, the period increases by 1 s. Then the value of m is
View Solution
