Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
The correct Answer is:A, B, C, D
(a) The mass B is moving
in a ciruclar path centred at
A. The centripetal force
(mlω2)required for this
circular motion is provided by
F'. Therefore a force F' acts
on A (the hinge) which is
equal to mIω2. The same is the case for mass C.
Therefore the net force on the
hinge is
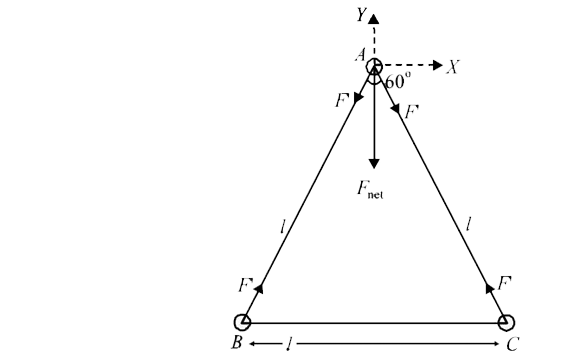
F≠t=√F'2+F2+2F'F'cos60∘
F≠t=√2F'2+2F'2×12=√3F'=√3lω2
(b) The force F acting on B Will probide a torque to the system. This torque is F×l√32=Iα
F×x√3l2=(2ml2)α
⇒α=√34×(Fml)
The total force acting on the system along x-direction is
F+(F≠t_x
This force is responsible for giving an acceleration ax to the system.
Therefore,
F+(F≠t)x=3m(ax)cm.
=3mF4m⟨.αx=αr=√34F□ml×l√3=F4)<br>(3F)/(4) :. (F_net) = - (F)/(4)<br>(F_(net))_y remains the same as before = sqrt3mlomega^2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View SolutionThree equal masses m are rigidly connected to each other by massless rods of length l forming and equilateral triangle, as shown above. The assembly is to be given an angular velocity ω about an axis perpendicular to the triangle. For fixed ω, what is the ratio of the kinetic energy of the assembly for an axis through Bt compared with that for an axis through A.
 .
.
View Solution
Knowledge Check
Three particles each of mass m are placed at the three corners of an equilateral triangle of side L. A particle of mass M is kept at the midpoint of any one side. What is the force acting on M, due to this system of 3 particles ?
AGMm4L2B34GMmL2C43GMmL2D4GMmL2The angular velocity of a rigid body about any point of that body is same :
Aonly in magnitudeBonly in directionCboth in magnitude and direction necessarilyDboth in magnitude and direction about some points but not about all points.Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3L
Three point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particles A,B,C of mass m each are joined to each other by massless rigid rods to form an equilateral triangle of side a. Another particle of mass m hits B with a velocity v0 directed along BC as shown. The colliding particle stops immediately after impact.
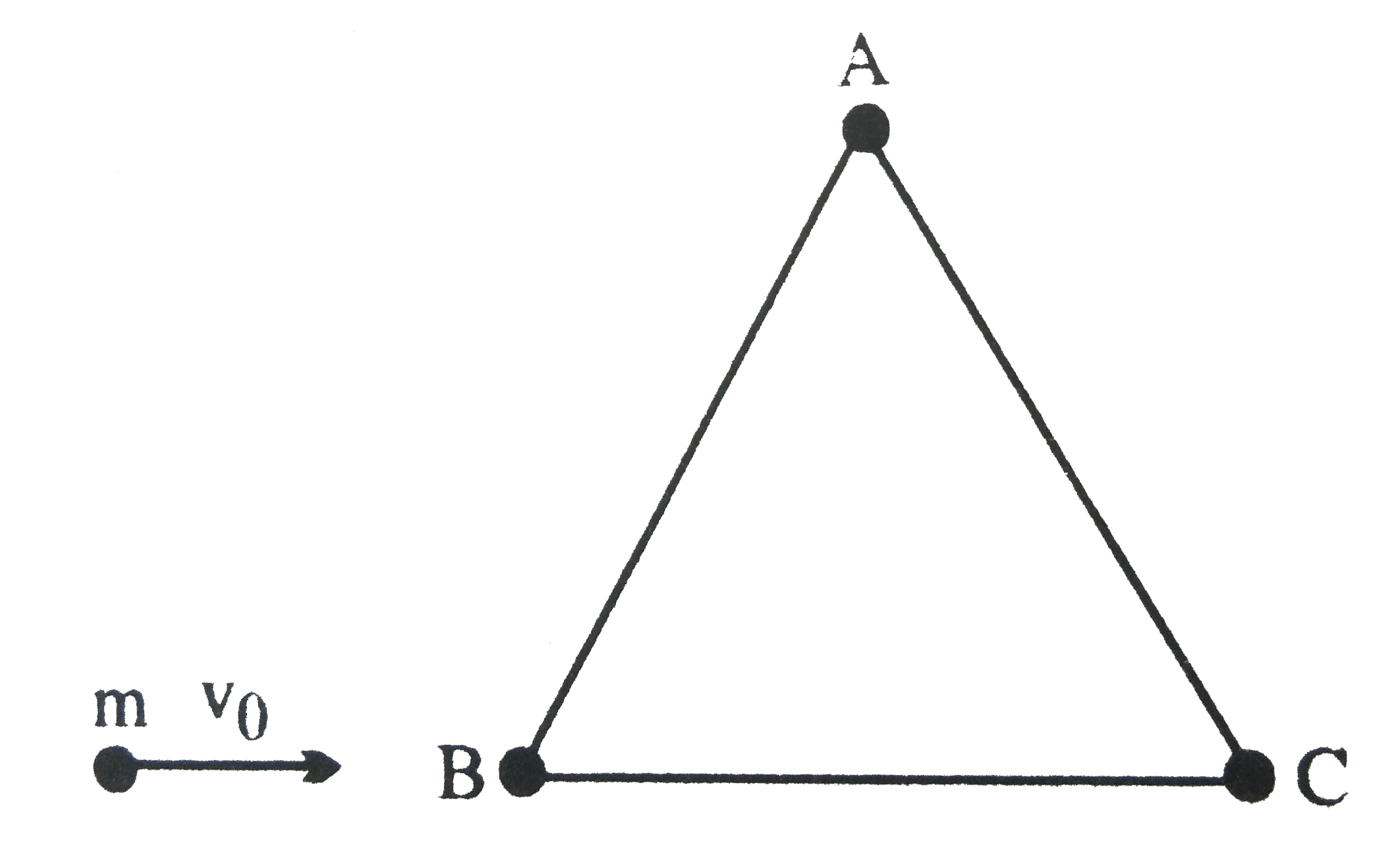
(i) Calculate the time required by the triangle ABC to complete half-revolution in its subsequent motion.
(ii) What is the net displacement of point B during this interval ?
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree point masses, each of mass m, are placed at the corners of an equilateral triangle of side L. The moment of inertia of this system about an axis along one side of the triangle is
View Solution
