Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizontal frictionless table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
a. The centre of mass of the system is at the centroid of a triangular assembly. The CM moves along a cirular path with constant angular velocity. Therefore, there must be a horizontal centripetal fore directed towards the axis at the hinge.
From figure a and we find
AD=lsin60∘(l√32)
AO=23AD=l2√3=r
The centripetal acceleration ac=ω2r=ω2(l√3)
Tangential acceleration a1=αr=α(l√3)
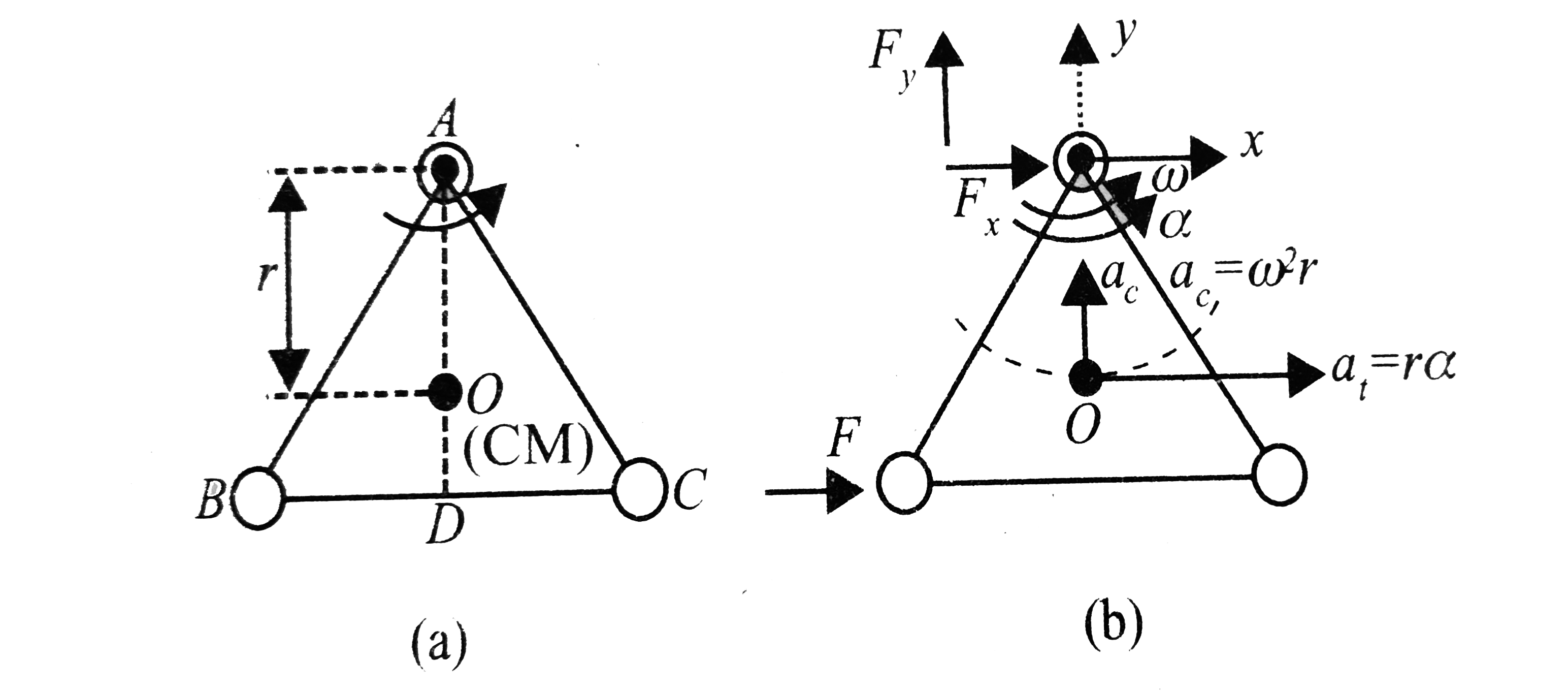
b. Let Fx and Fy be the forces applied by the hinges along x-axis and y-axis, respectively. The system is in non centroidal rotation. The three equations of motion are
ΣFx=Fx+F=(3m)at=3m(l√3α).........i
SigmFy=Fy=3m(l√3)ω2............ii
Στ=F×(√32l)=2ml2α .............iii
From eqn ii α=√3F4ml
From eqn i Fx+F=3m(1√3α)×√3F4ml=3F4
⇒Fx=F4
From eqn ii Fy=√3mlω2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.
View SolutionAll the rigid bodies lie in smooth horizontal plane.

View Solution
Knowledge Check
Three point masses each of mass m are joined together using a string to form an equilateral triangle of side a. The system is placed on a smooth horizontal surface and rotated with a constant angular velcoity ω about a vertical axis passing through the centroid Then the tension in each string is .
Amaω2B3maω2Cmaω23Dmaω2√3Three particles each of mass m are placed at the three corners of an equilateral triangle of side L. A particle of mass M is kept at the midpoint of any one side. What is the force acting on M, due to this system of 3 particles ?
AGMm4L2B34GMmL2C43GMmL2D4GMmL2The angular velocity of a rigid body about any point of that body is same :
Aonly in magnitudeBonly in directionCboth in magnitude and direction necessarilyDboth in magnitude and direction about some points but not about all points.
Three equal masses m are rigidly connected to each other by massless rods of length l forming and equilateral triangle, as shown above. The assembly is to be given an angular velocity ω about an axis perpendicular to the triangle. For fixed ω, what is the ratio of the kinetic energy of the assembly for an axis through Bt compared with that for an axis through A.
 .
.
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particles A,B,C of mass m each are joined to each other by massless rigid rods to form an equilateral triangle of side a. Another particle of mass m hits B with a velocity v0 directed along BC as shown. The colliding particle stops immediately after impact.
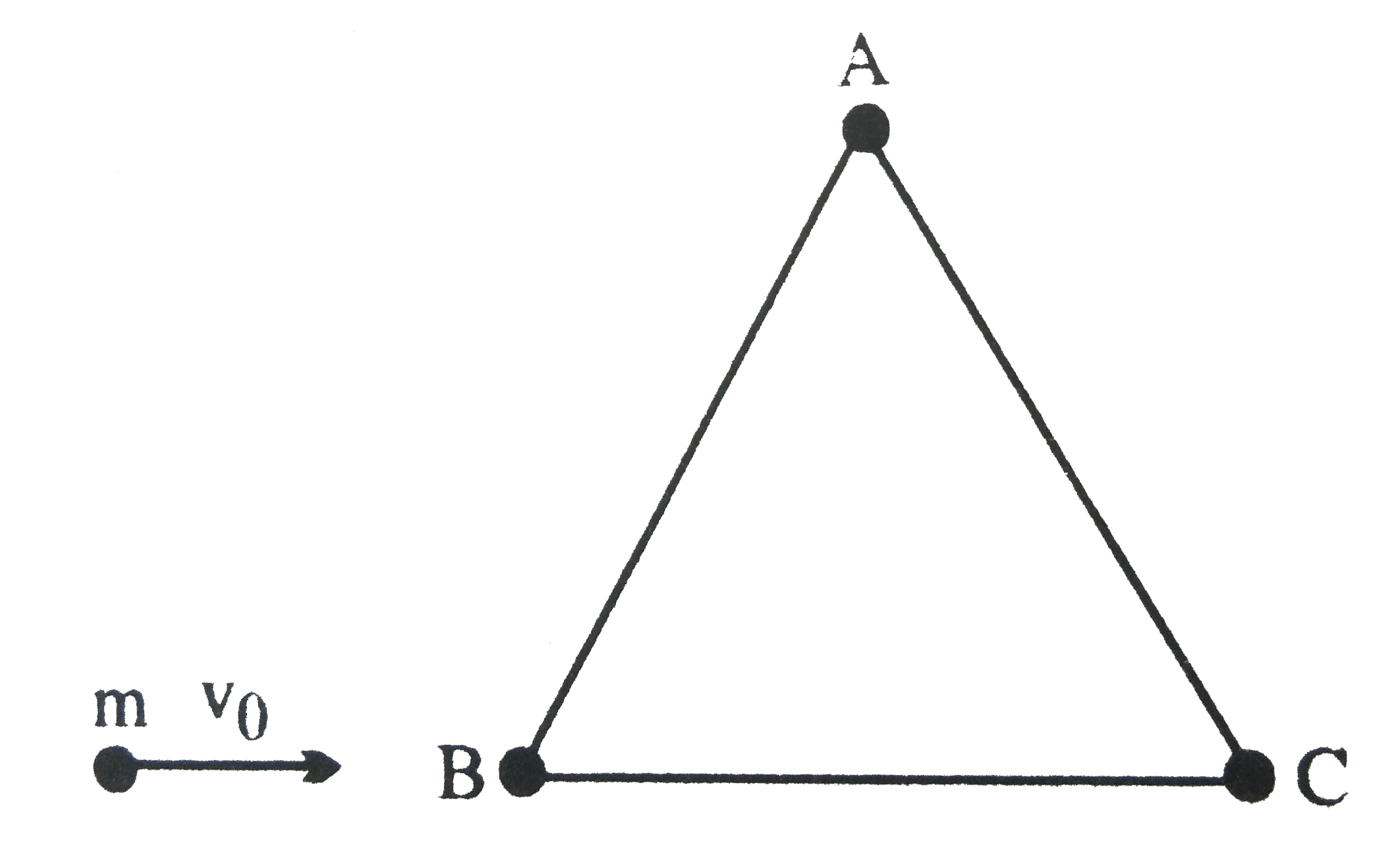
(i) Calculate the time required by the triangle ABC to complete half-revolution in its subsequent motion.
(ii) What is the net displacement of point B during this interval ?
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View Solution
