Three rods of equal of length are joined to from an equilateral triangle ABC. D is the midpoint of AB. The coefficient of linear expansion is α1 for AB and α2 for AC and BC . If the distance DC remains constant for small changes in temperature,

α1=α2
α1=2α2
α1=4α2
α1=1/2α2
The correct Answer is:C
h2=l2−l24 (i)
At small change in temperature
h2=[l(1+α2Δθ)]2−[l2(1+α1Δθ)]2
=l2(1+2α2Δθ)−l24(1+2α1Δθ)
l2−l24=l2+2α2l2Δθ−l24−2α1l24Δθ
α2=a14⇒α1=4α2 .
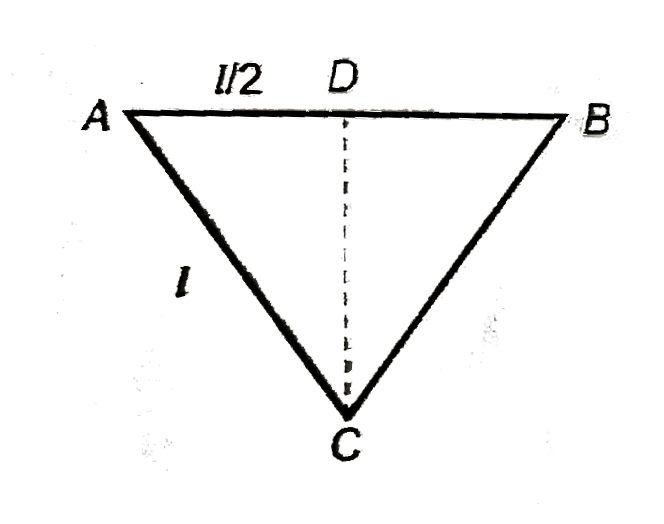
Topper's Solved these Questions
- TEMPERATURE AND THERMAL EXPANSIONBOOK - CP SINGHCHAPTER - TEMPERATURE AND THERMAL EXPANSIONEXERCISE - EXERCISES
64 Videos
- SOUND WAVESBOOK - CP SINGHCHAPTER - SOUND WAVESEXERCISE - Exercises
130 Videos
- UNITS, DIMENIONS AND MEASUREMENTSBOOK - CP SINGHCHAPTER - UNITS, DIMENIONS AND MEASUREMENTSEXERCISE - Exercises
63 Videos
Similar Questions
The coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
View SolutionThree rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.

View Solution
Knowledge Check
An equilateral triangle ABC is formed by joining three rods of equal length and D is the mid-point of AB. The coefficient of linear expansion for AB is α1 and for AC and BC is α2. The relation between α1 and α2, if distance DC remains constant for small changes in temperture is
_E01_117_Q01.png) Aα1=α2Bα1=4α2Cα2=4α1Dα1=12α2
Aα1=α2Bα1=4α2Cα2=4α1Dα1=12α2Two rods , one of aluminium and the other made of steel, having initial length l1 and l2 are connected together to from a sinlge rod of length l1+l2 . The coefficient of linear expansion for aluminium and steel are αa and αs for AC and BC . If the distance DC remains constant for small changes in temperature,
AαsαaBαaαsCαs(αa+αs)Dαa(αa+αs)Three rods of equal l are joined to from an equilateral triangle PQR.O is the mid-point of PQ. Distance OR remains same for small change in temperature. Coefficient of linear expansion for PR and RQ is same i.e., α2 but for PQ is α1. Then
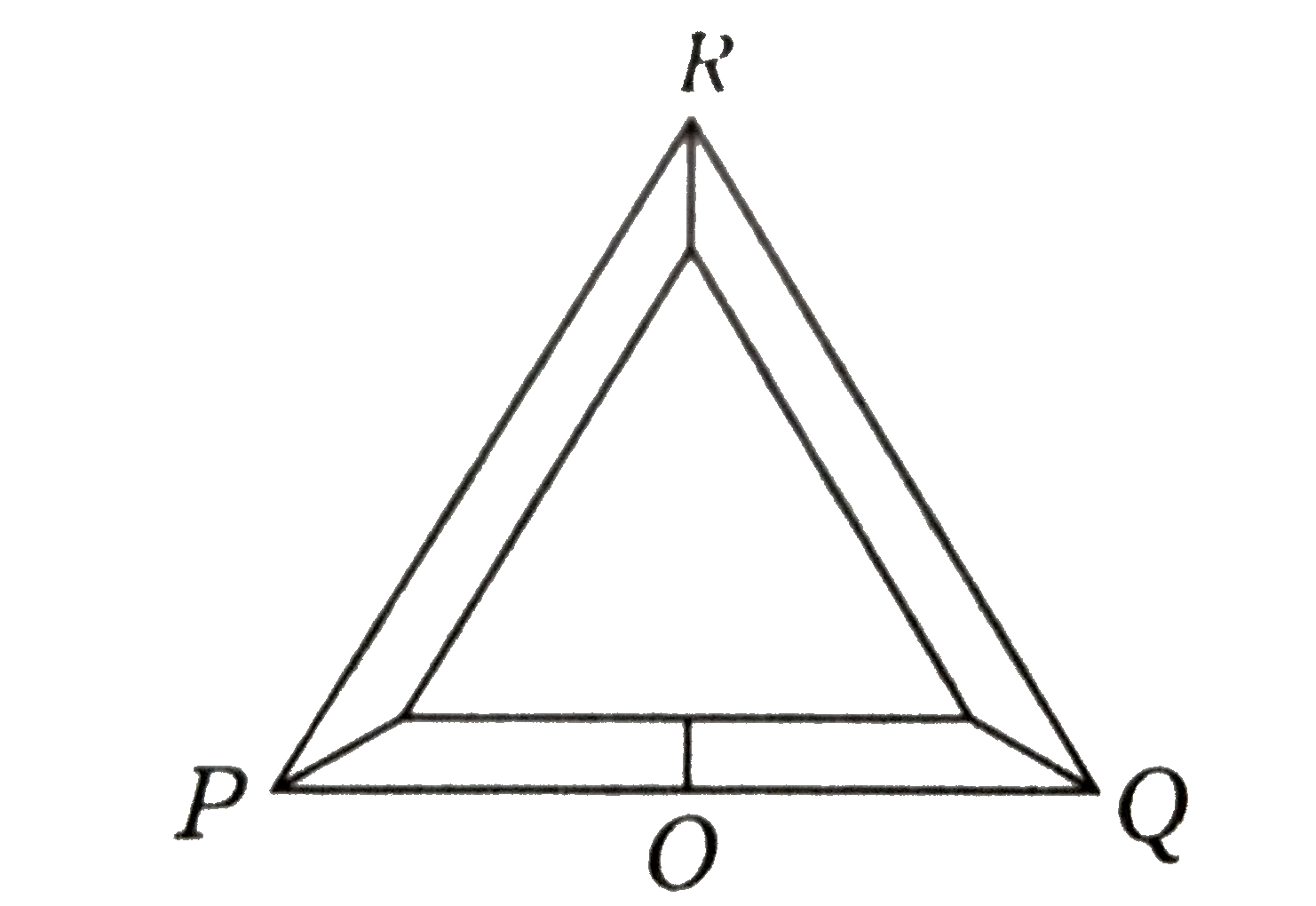 Aα2=3α1Bα2=4α1Cα1=3α2Dα1=4α2
Aα2=3α1Bα2=4α1Cα1=3α2Dα1=4α2
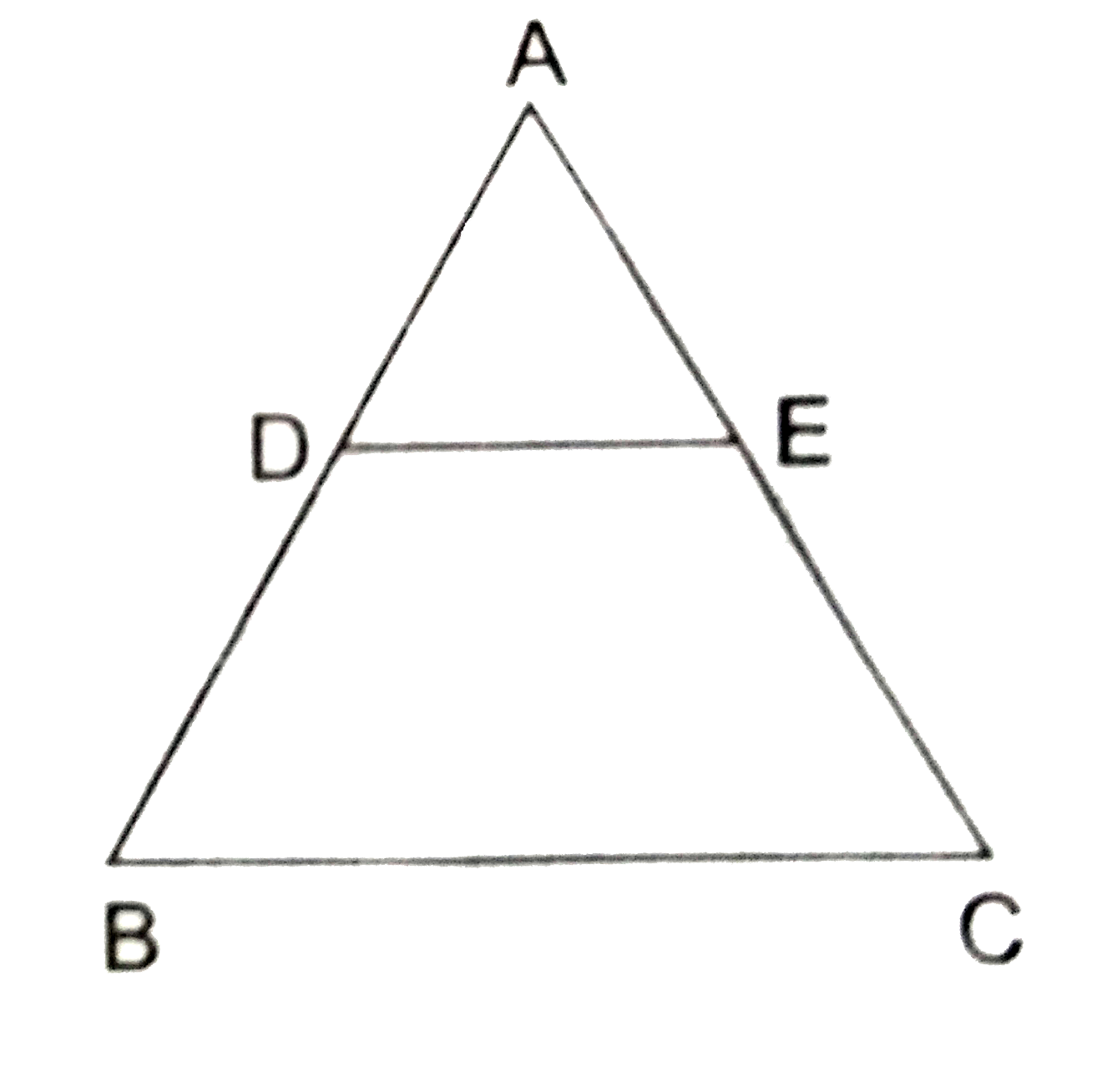
In an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
View SolutionThe coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
View SolutionIf L1 and L2 are the lengths of two rods of coefficients of linear expansion α1 and α2 respectively the condition for the difference in lengths to be constant at all temperatures is
View Solution
The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will be
View SolutionThe coefficient of linear expansion of a rod is α and its length is L. The increase in temperature required to increase its legnth by 1% is
View Solution
