Three travelling waves are superimposed. The equations of the wave are
$y_{!} = A_{0} sin (k x - ω t), y_{2} = 3 \sqrt{2} A_{0} sin (k x - ω t + ϕ)$ and $y_{3} = 4 A_{0} cos (k x - ω t)$
find the value of $ϕ (given 0 \leq ϕ \leq π / 2)$ if the phase difference between the resultant wave and first wave is $π / 4$

A

$\frac{π}{6}$

B

$\frac{π}{3}$

C

$\frac{π}{12}$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given, $y_{1} = A_{0} sin (k x - ω t)$
$y_{2} = 3 \sqrt{2} A_{0} sin (k x - ω t + ϕ),$
and $y_{3} = 4 A_{0} cos (k x - ω t)$ ,

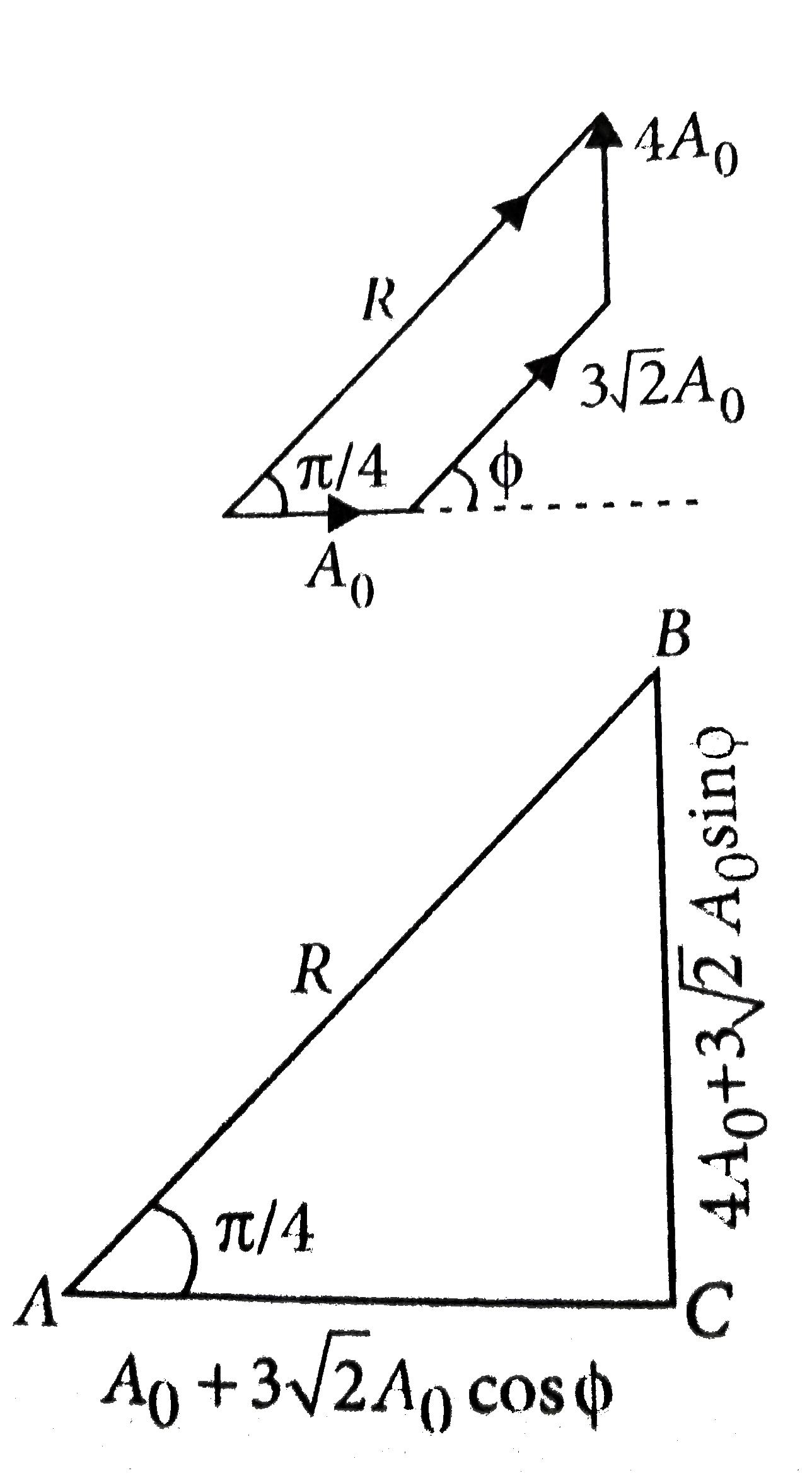
These waves can be represented by phase diagram as shown.
From phase diagram,
$tan (\frac{π}{4}) = \frac{B C}{A C} = \frac{A_{0} (4 + 3 \sqrt{2} sin ϕ)}{A_{0} (1 + 3 \sqrt{2} cos ϕ)}$
$\Rightarrow 4 + 3 \sqrt{2} sin ϕ = 1 + 3 \sqrt{2} cos ϕ$
$\Rightarrow cos ϕ - sin ϕ = \frac{1}{\sqrt{2}}$
Squaring both sides, we get
${cos}^{2} ϕ + {sin}^{2} ϕ - 2 sin ϕ cos ϕ = \frac{1}{2}$
$1 - 2 sin ϕ cos ϕ = \frac{1}{2} or 2 ϕ = \frac{π}{6} \Rightarrow ϕ = \frac{π}{12}$

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two sinusoidal waves are superposed. Their equations are
$y_{1} = A sin (k x - ω t + \frac{π}{6}) and y_{2} = A sin (k x - ω t - \frac{π}{6})$
the equation of their resultant is
A $\frac{A}{\sqrt{3}} sin (k x - ω t)$
B $A \sqrt{3} sin (k x - ω t)$
C $A \sqrt{3} sin (k x - ω t - \frac{π}{3})$
D $\frac{A}{\sqrt{3}} sin (k x - ω t - \frac{π}{2})$
Question 2 - Select One
Three waves $y_{1}, y_{2}, y_{3}$ are given by $y_{1} = A sin (K x - ω t), y_{2} A = sin (K x + ω t) and y_{3} = A sin (K y - ω t)$ . Which one of the following represents wave ?
A $y_{1} + y_{2} + y_{3}$
B $y_{1} + y_{3}$
C $y_{1} + y_{2}$
D $y_{2} + y_{3}$
Question 3 - Select One
Two waves are represented by
$Y_{1} = a_{1} cos (ω t - k x) and Y - 2 = a_{2} sin (ω t - k x + π / 3)$
Then the phase difference between them is-
A $\frac{π}{3}$
B $\frac{π}{2}$
C $\frac{5 π}{6}$
D $\frac{π}{6}$

NCERT FINGERTIPS-WAVES-Higher Order Thinking Skills

Home
Ask Doubt
Profile