Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.

Video Solution

Text Solution

Verified by Experts

As per question, three point masses, each of mass $M$ are lying at the vertices of an equilaternal triangle of side $2 R$ , Fig.

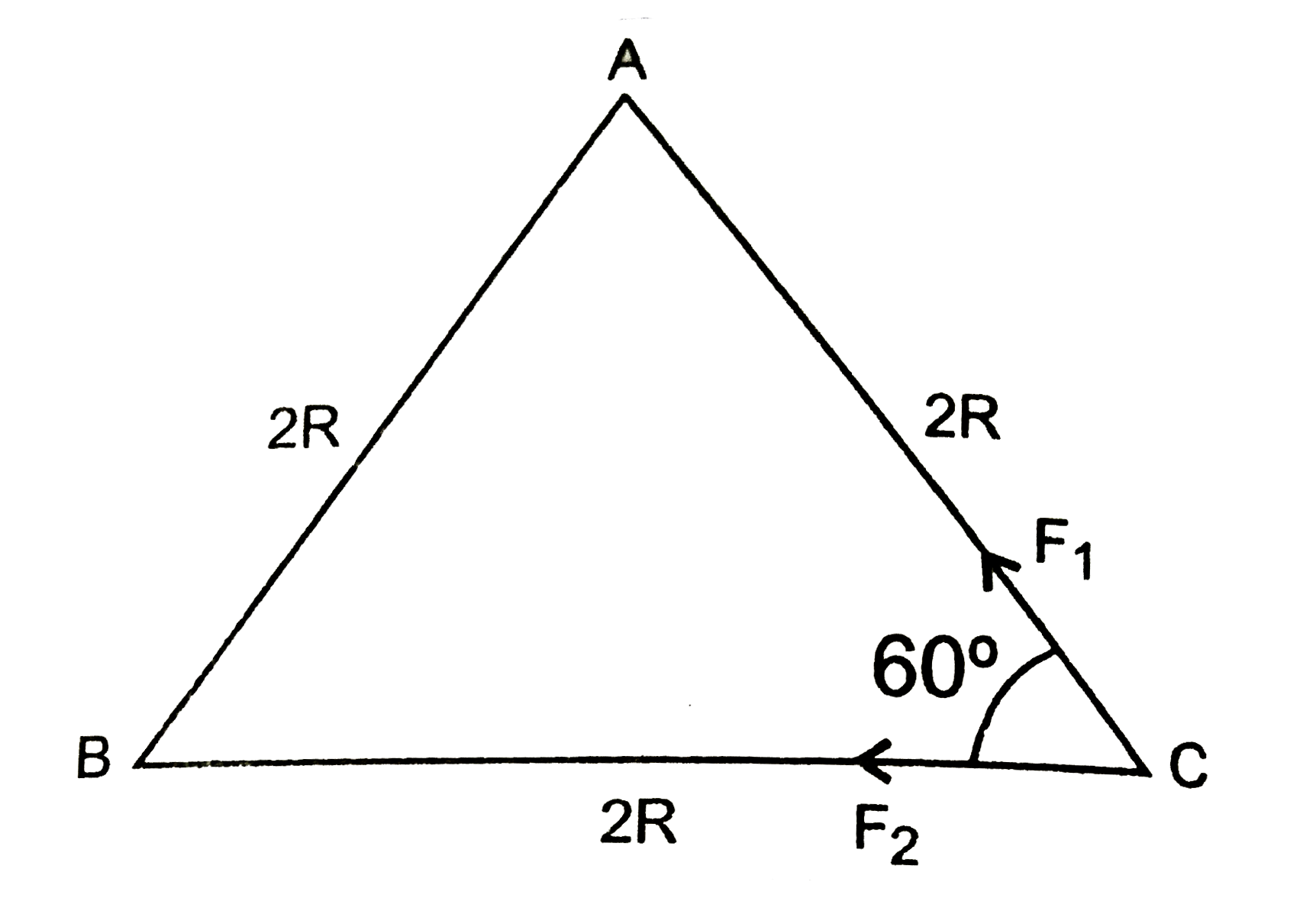
Force of attraction on sphere $C$ due to sphere $A$
is $F_{1} = \frac{G m \times m}{{(2 R)}^{2}} = \frac{G m^{2}}{4 R^{2}}$ along $C A$
Force of attraction on sphere $C$ due to sphere $B$
is $F_{2} = \frac{G m \times m}{{(2 R)}^{2}} = \frac{G m^{2}}{4 R^{2}}$ along $C B$
These force $- \to F_{1}$ and $- \to F_{2}$ are inclined at an angule $60^{\circ}$
So the resultant force on sphere $C$ is
$F = \sqrt{F_{1}^{2} + F_{2}^{2} + 2 F_{1} F_{2} {cos 60}^{\circ}}$
$= \sqrt{F_{1}^{2} + F_{1}^{2} + 2 F_{1} F_{1} \times 1 / 2}$
$= \sqrt{3} F_{1} = \frac{\sqrt{3}}{4} \frac{G m^{2}}{R^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three uniform spheres each of mass $m$ and diameter $D$ are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
A $\frac{3 G m^{2}}{D^{2}}$
B $\frac{2 \sqrt{3} G m^{2}}{D^{2}}$
C $\frac{\sqrt{3 G m^{2}}}{4 D^{2}}$
D $\frac{\sqrt{3} G m^{2}}{D^{2}}$
Question 2 - Select One
Three identical spheres, each having a charge q and radius R. are kept in such a way that each touches the other two. The magnitude of the electric force on any sphere due to the other two is
A $\frac{1}{4 π ε_{0}} {(\frac{q}{R})}^{2}$
B $\frac{\sqrt{3}}{4 π ε_{0}} {(\frac{q}{R})}^{2}$
C $\frac{\sqrt{3}}{16 π ε_{0}} {(\frac{q}{R})}^{2}$
D $\frac{\sqrt{5}}{16 π ε_{0}} {(\frac{q}{R})}^{2}$
Question 3 - Select One
Three uniform spheres, A, B and C each of mass M and radius R are kept in such a way that each sphere touches the other two. What is the magnitude of the gravitational force acting on A due to B and C ?
A $\frac{\sqrt{3} G M^{2}}{4 R^{2}}$
B $\frac{\sqrt{3} G M^{2}}{R^{2}}$
C $\frac{3 G M^{2}}{4 R^{2}}$
D $\frac{\sqrt{3} G M^{2}}{2 R}$

PRADEEP-GRAVIATION-CONCEPTUAL PROBLEMS

Home
Ask Doubt
Profile