Three vectors →A,→B and →C add up to zero.Find which is false.
(→A×→B)×→C is not zero unless →B,→C are parallel.
(→A×→B)⋅→C is not zero unless →B,→C are parallel.
If →A,→B,→C define a plane, (→A×→B)×→C is in that plane.
(→A×→B)⋅→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣→C2=A2+B2.
The correct Answer is:C
Step by step video, text & image solution for Three vectors vecA,vecB and vecC add up to zero.Find which is false. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason15videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Higher Order Thinking Skills8videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason15videos
MOTION IN A STRAIGHT LINE
Similar Questions
Three vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionConsider three vectors →A,→Band→C as shown in fig. perform graphically the following vector additions and subtractions (a) →A+→B
(b). →A+→B+→C
(c). →A−→B
(d). →A+→B−→C
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a righht angled triangle the three vectors →a,→b and →c add to zero. Then →a,→b is
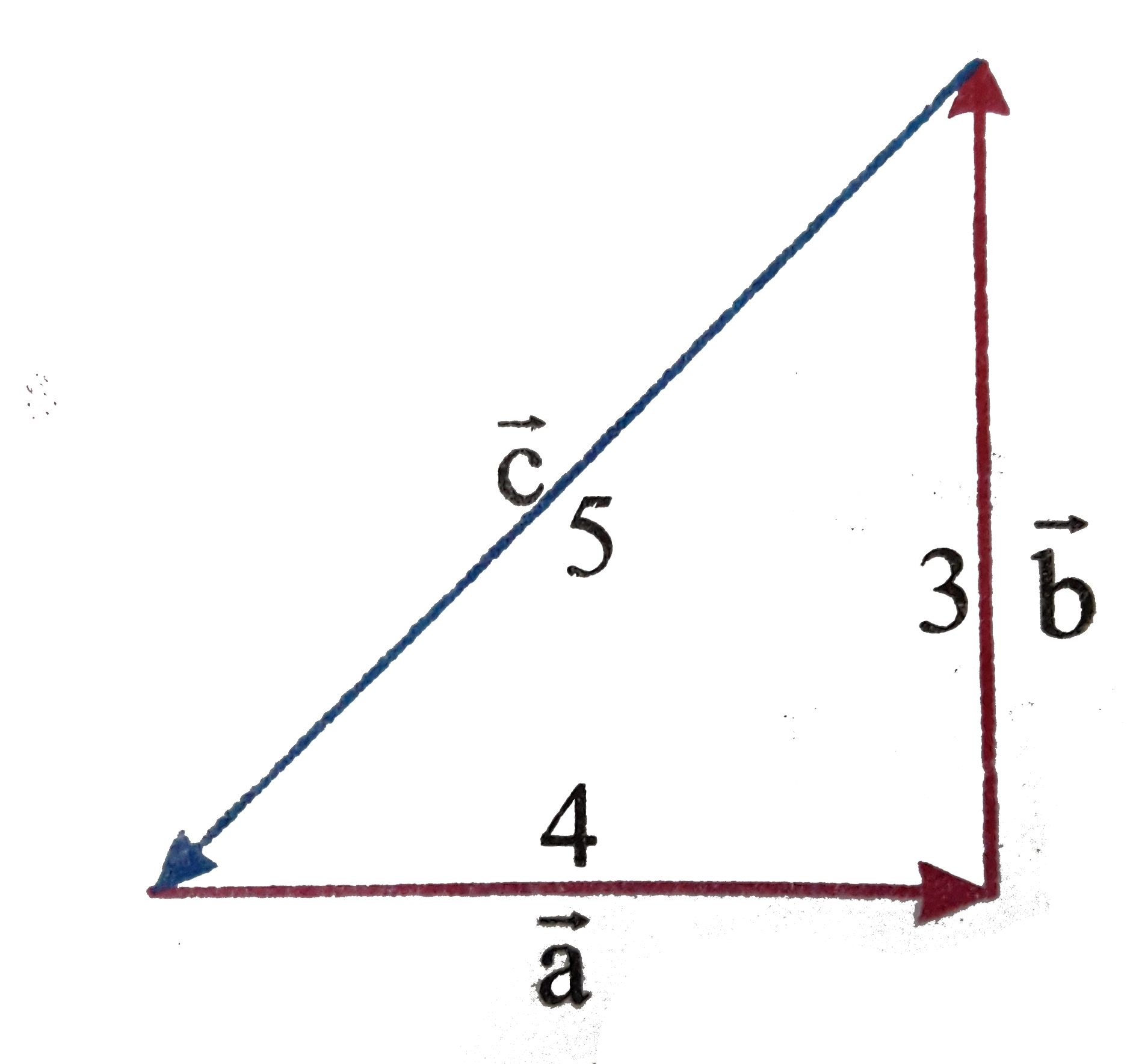 A−9B+9C0D−3
A−9B+9C0D−3 - Question 2 - Select One
The vector sum of three vectors→A,→B and →C is zero . If ˆi and ˆj are the unit vectores in the vectors in the directions of →A and →B respectively , them :
A→C is in the plane of ˆi of ˆjB→C is along ˆi׈jC→C is along ˆiD→C is alongˆj - Question 3 - Select One
Three vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
A→BB→CC→B.→CD→B×→C
Three vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
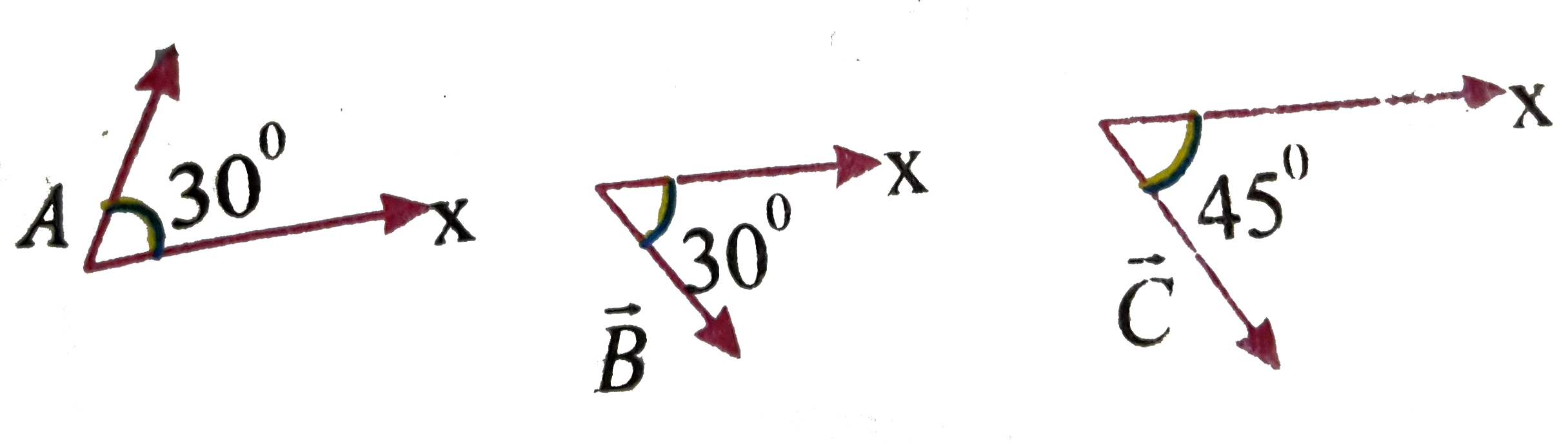 View Solution
View SolutionGiven three vectors e→a,→band→c two of which are non-collinear. Futrther if (→a+→b) is collinear with →c,(→b+→c) is collinear with →a,|→a|=∣∣→b∣∣=|→c|=√2 find the value of →a.→b+→b.→c+→c.→a
View SolutionGiven three vectors →a,→b and →c are non-zero and non-coplanar vectors. Then which of the following are coplanar.
View SolutionIf three vectors →A,→Band→C satisfy the relation →A.→B=0&→A.→C=0 then the vector →A is parallel to →B×→C.
Statement-2 : →A⊥→B and →A⊥→C hence A is perpendicular to plane formed by →Band→C.View SolutionThree vectors →a,→b and →c satisfy the relation →a.→b=0 and →a.→c=0. The vector →a is parallel to
View Solution

