Three vectors →A,→B and →C add up to zero.Find which is false.
(→A×→B)×→C is not zero unless →B,→C are parallel
(→A×→B).→C is not zero unless →B,→C are parallel
If →A,→B,→C define a plane , (→A×→B)×→C is in that plane
(→A×→B).→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣ if C2=A2+B2
The correct Answer is:B
(b): Since →A+→B+→C=0
which means that →A,→Band→C are coplanar . Option (a): (→A×→B)×→C=→A.(→B×→C)
If →Band→C are parallel, then →A.(→B×→C)=0 or →A×(→B×→C)=→0and(→A×→B)×→C≠o if →Band→C are not parallel . Option (a) is correct option (b): For three coplanar vectors,
→A×→B→C=(→B×→C).→A if B | | C, then →B×→C=0
∴(→B×→C).→A=0⇒ option (b) is false.
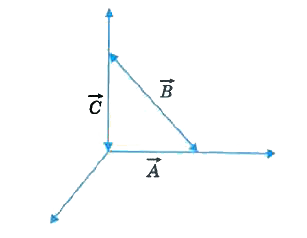
Option (c): Since →A+→B+→C=0 , so they from a triangle as show in the figure and hence →A,→B,→C define a plane (→A×→B)×→C.
Option (d):
For three coplanar vectors, (→A.×→B).→C=0 always
If C2=A2+B2
And →A+→B+→c=0 already
This implies that A and B are mutually perpendicular to each other .
(→A×→B).→C=(ABsin90∘ˆP).→C
=ABCcos90∘=0
(Angle between unit vector ˆPandˆC is also 90∘).
Option (d) is not correct.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS)
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Three vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionConsider three vectors →A,→Band→C as shown in fig. perform graphically the following vector additions and subtractions (a) →A+→B
(b). →A+→B+→C
(c). →A−→B
(d). →A+→B−→C

View Solution
Knowledge Check
In a righht angled triangle the three vectors →a,→b and →c add to zero. Then →a,→b is
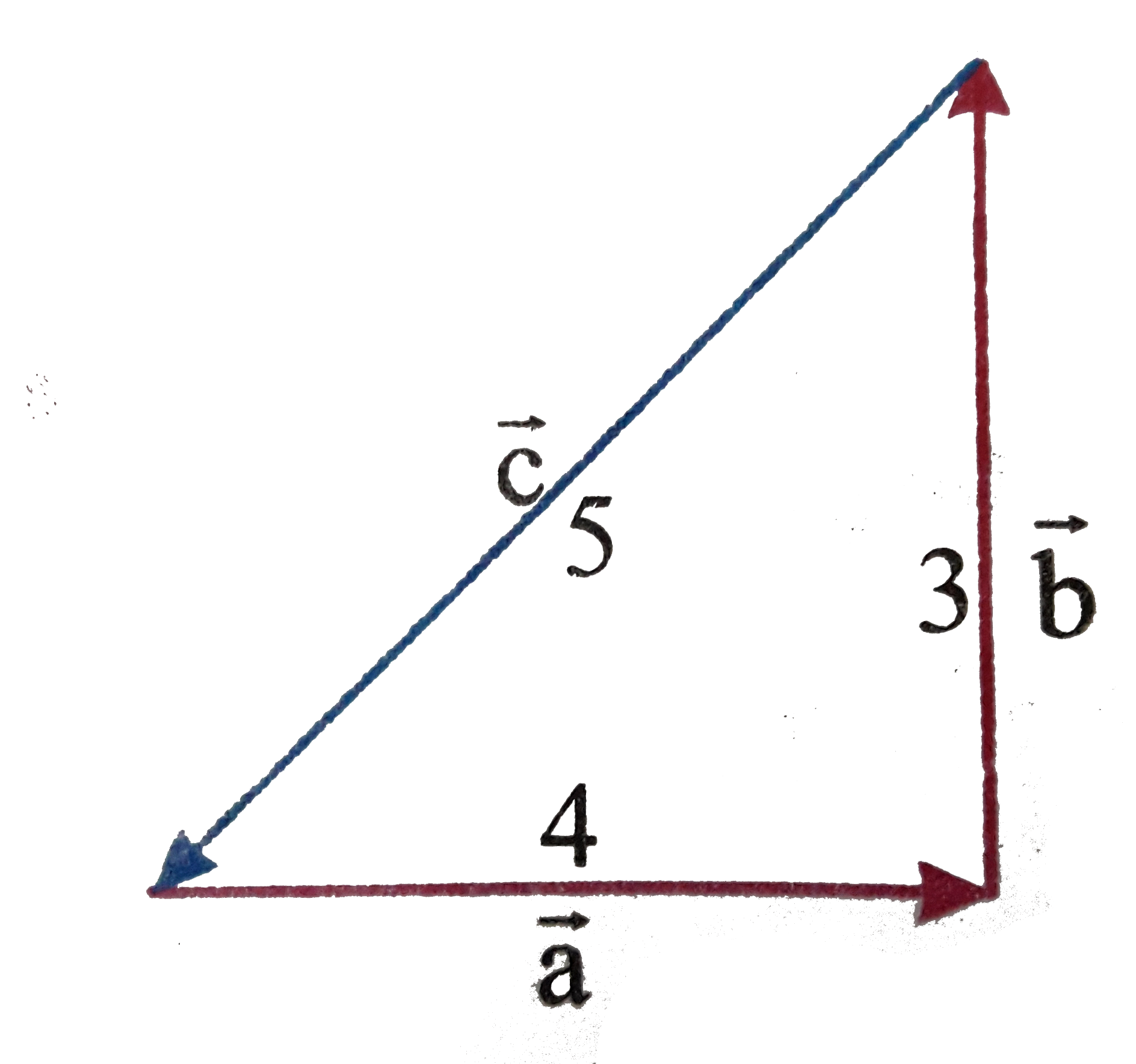 A−9B+9C0D−3
A−9B+9C0D−3The vector sum of three vectors→A,→B and →C is zero . If ˆi and ˆj are the unit vectores in the vectors in the directions of →A and →B respectively , them :
A→C is in the plane of ˆi of ˆjB→C is along ˆi׈jC→C is along ˆiD→C is alongˆjThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
A→BB→CC→B.→CD→B×→C
Three vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
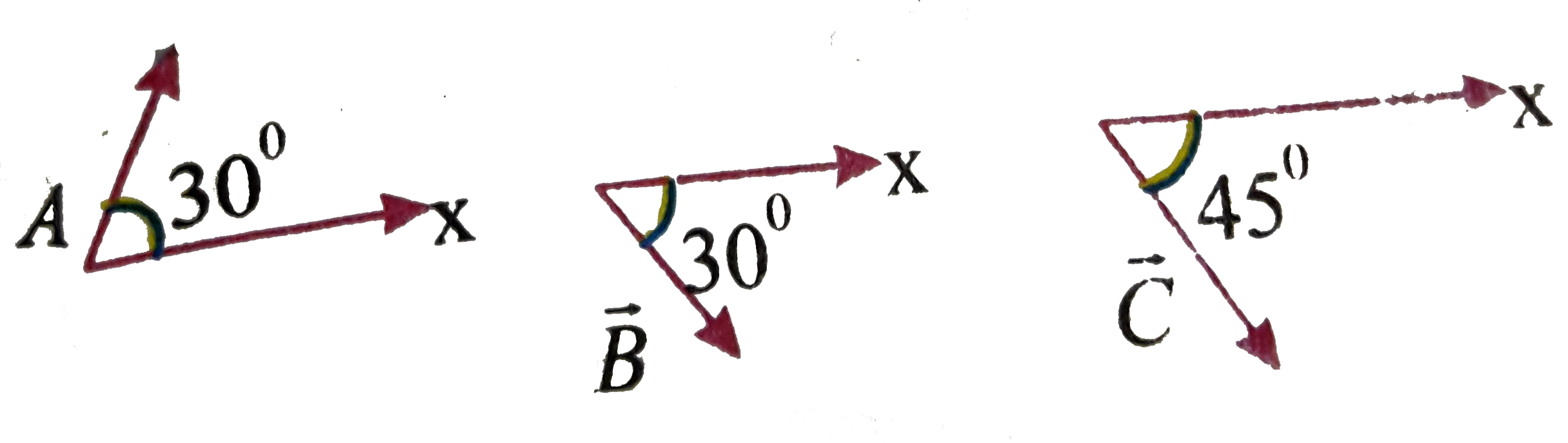
View SolutionGiven three vectors e→a,→band→c two of which are non-collinear. Futrther if (→a+→b) is collinear with →c,(→b+→c) is collinear with →a,|→a|=∣∣→b∣∣=|→c|=√2 find the value of →a.→b+→b.→c+→c.→a
View SolutionGiven three vectors →a,→b and →c are non-zero and non-coplanar vectors. Then which of the following are coplanar.
View SolutionIf three vectors →A,→Band→C satisfy the relation →A.→B=0&→A.→C=0 then the vector →A is parallel to →B×→C.
Statement-2 : →A⊥→B and →A⊥→C hence A is perpendicular to plane formed by →Band→C.
View SolutionThree vectors →a,→b and →c satisfy the relation →a.→b=0 and →a.→c=0. The vector →a is parallel to
View Solution
