To determine the Young's modulus of a wire, the formula is Y=FA×LΔL, where L = length, A = area of cross-section of the wire, ΔL = change in length of the wire when stretched with a force F. The conversion factor to change it from CGS to MKS system is
1
10
0.1
0.01
To determine the conversion factor for Young's modulus from the CGS (centimeter-gram-second) system to the MKS (meter-kilogram-second) system, we will analyze the formula for Young's modulus and the units involved.
1. Understand the Formula for Young's Modulus:
The formula for Young's modulus (Y) is given by:
Y=FA×LΔL
where:
- F = Force applied (in Newtons in MKS, Dynes in CGS)
- A = Area of cross-section (in m² in MKS, cm² in CGS)
- L = Original length of the wire (in meters in MKS, centimeters in CGS)
- ΔL = Change in length (in meters in MKS, centimeters in CGS)
2. Identify the Units in CGS:
- Force in CGS: 1 Dyne = 10−5 Newton
- Area in CGS: 1 cm² = 10−4 m²
- Length in CGS: 1 cm = 10−2 m
3. Convert Each Component:
- For force F:
F (in CGS)=1 Dyne=10−5 Newton
- For area A:
A (in CGS)=1 cm2=10−4 m2
- For length L and change in length ΔL:
L (in CGS)=1 cm=10−2 m
ΔL (in CGS)=1 cm=10−2 m
4. Substituting the Units into the Formula:
Now, substituting these conversions into the Young's modulus formula:
Y=10−5 N10−4 m2×10−2 m10−2 m
5. Simplifying the Expression:
The change in length cancels out:
Y=10−510−4=10−1 N/m2=0.1 N/m2
6. Conclusion:
The conversion factor from CGS to MKS for Young's modulus is 0.1.
Final Answer:
The conversion factor to change Young's modulus from CGS to MKS system is 0.1.
The formula for Young's modulus (Y) is given by:
Y=FA×LΔL
where:
- F = Force applied (in Newtons in MKS, Dynes in CGS)
- A = Area of cross-section (in m² in MKS, cm² in CGS)
- L = Original length of the wire (in meters in MKS, centimeters in CGS)
- ΔL = Change in length (in meters in MKS, centimeters in CGS)
- Force in CGS: 1 Dyne = 10−5 Newton
- Area in CGS: 1 cm² = 10−4 m²
- Length in CGS: 1 cm = 10−2 m
- For force F:
F (in CGS)=1 Dyne=10−5 Newton
- For area A:
A (in CGS)=1 cm2=10−4 m2
- For length L and change in length ΔL:
L (in CGS)=1 cm=10−2 m
ΔL (in CGS)=1 cm=10−2 m
Now, substituting these conversions into the Young's modulus formula:
Y=10−5 N10−4 m2×10−2 m10−2 m
The change in length cancels out:
Y=10−510−4=10−1 N/m2=0.1 N/m2
The conversion factor from CGS to MKS for Young's modulus is 0.1.
The conversion factor to change Young's modulus from CGS to MKS system is 0.1.
Topper's Solved these Questions
Similar Questions
To determine the young's modulus of a wire , the formula is Y=FA.LΔl , where L = l ength ,A = area of cross - section of the wire , ΔL = change in the length of the wire when streched with a force F. Find the conversion factor to change it from CGS t o MKS system.
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View Solution
Knowledge Check
In CGS system, the Young's modulusm of a steel wire is 2×1012. To double the length of a wire of unit cross-section area, the force
A4×106 dynesB2×1012 dynesC2×1012 newtonsD2×108 dynesThe resistance of wire of length l and area of cross-section a is x ohm. If the wire is stretched to double its length, its resistance would become:
A2 x ohmB0.5 x ohmC4 x ohmD6 x ohmA load w is suspended from a wire of length l and area of cross-section A. Change in length of the wire is say Δl. Change in length Δl can be increased to two times by increasing
Aw by two timesBl by two timesCA by two timesDA by four times
A wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
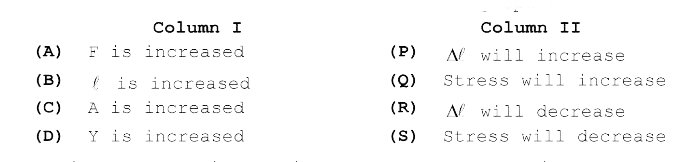
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionY is the Young's modulus of the material of a wire of length L and cross-sectional area A. It is stretched through a length l. What is the force constant of the wire?
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View Solution
