Total internal reflection of light ray from cylindrical optical fiber
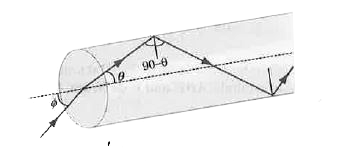
An optical fiber consists of a cylindrical core of unknown refractive index kept in air. A ray of light is incident on the flat face of the core so that it gets totally reflected at the curved surface (Fig.34-19). What is the possible refractive index if the ray is totally reflected at any angle of incidence $ϕ$ from air ?

Text Solution

Verified by Experts

When a ray refracts from air to glass, total internal reflection cannot occur. However, when this ray strikes curved surface of the fiber, the incidence is from denser to rarer medium. If n is such that total internal reflection occurs at this point, it will continue to occur as the ray strikes the curved surface repetedly at the same angle.
Calculation : Let us assume that the ray is incident at an angle $ϕ$ from air and is refracted into the cylinder at an angle $θ$ . It is then again incident on the air cylinder boundary at the curved surface as shown in Fig. 34-19 . The condition is that the ray should undergo total internal reflection at the face.
For this the angle of incidence here should be greater than critical angle.
$90^{\circ} - θ > θ_{c}$
Since sine is an increasing function, taking sine of both sides will not change the inequality.
$sin (90^{\circ} - θ) > {sin θ}_{c} = \frac{1}{n} (n {sin θ}_{c} = 1 \times {sin 90}^{\circ})$
$cos θ \geq \frac{1}{n}$
Again, applying Snell.s law at flat face, we get
$1 \times sin ϕ = n \times sin θ$
Squaring and adding , we get
$n^{2} {sin}^{2} θ + n^{2} {cos}^{2} θ \geq 1 + {sin}^{2} ϕ$
$n^{2} \geq 1 + {sin}^{2} ϕ$
But the maximum value of $sin ϕ$ is $1$ when the angle of incidence is $90^{\circ}$ . For this condition,
$n^{2} \geq 2$
or $n \geq \sqrt{2}$
Learn : Interestingly this yields $μ \geq 1.41$ . Thus, even ordinary glass can be used in optical fiber. But for practical reasons, this core is coated with a cylindrical shell called cladding. If cladding has refractive index of $μ_{1}$ , the condition on $μ_{2}$ is
$μ_{2} \geq \sqrt{μ_{1}^{2} + 1}$

A ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle $ϕ$ . If $μ$ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
A(a) $90^{\circ} + ϕ$
B(b) ${sin}^{- 1} (μ cos ϕ)$
C(c) $90^{\circ}$
D(d) $90^{\circ} - {sin}^{- 1} (sin ϕ / μ)$